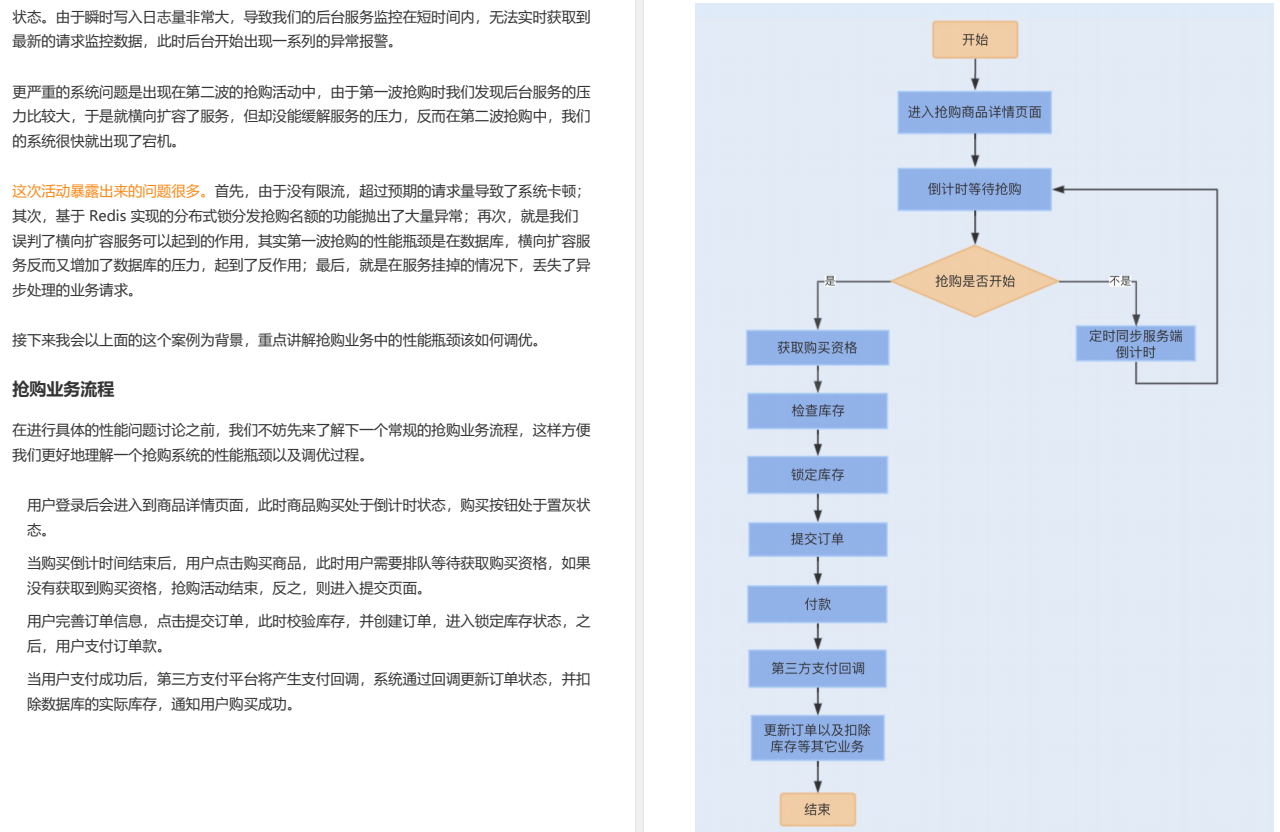
在之前的文章 DCDC 降压芯片基本原理及选型主要参数介绍 中已经大致讲解了dcdc降压电路的工作原理,今天再结合仿真将buck电路工作过程讲一讲。
基本拓扑
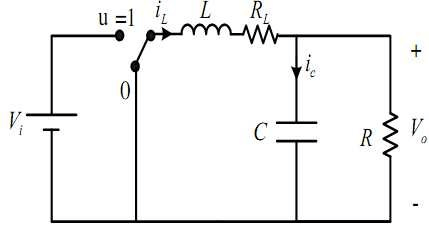
上图为buck电路的基本拓扑结构,开关打到1,电感充电;开关打到0,电感放电。通常认为电感和电容都是储能元件,但是电感的充放电是有能量形式的转换的,充电时电场 → 磁场,放电时磁场 → 电场。
接下来,我们结合仿真来看看buck电路的具体工作过程。
原理图
在kicad中建立仿真原理图:
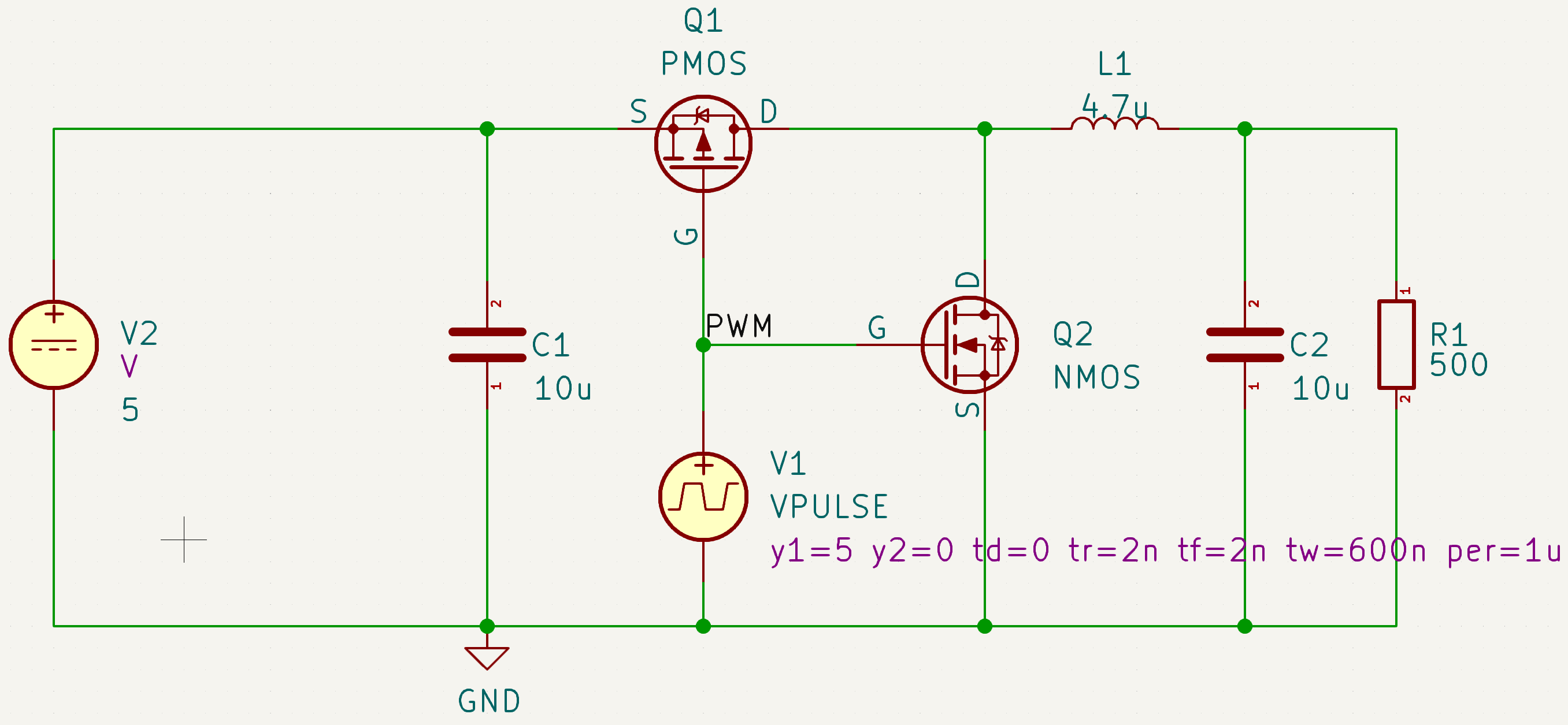
V2是直流电压源;Q1是PMOS;Q2是NMOS;V1是脉冲电压源,用它来做PWM控制信号;C1是输入电容;C2是输出电容;L1是储能电感;R1是负载电阻。
从图中可以看到,我们将PWM频率设置为1MHz,以便使用更小的电感进行仿真。
仿真工作过程
1. 启动
我们先进行10us的瞬态仿真,看下前10个周期的波形:
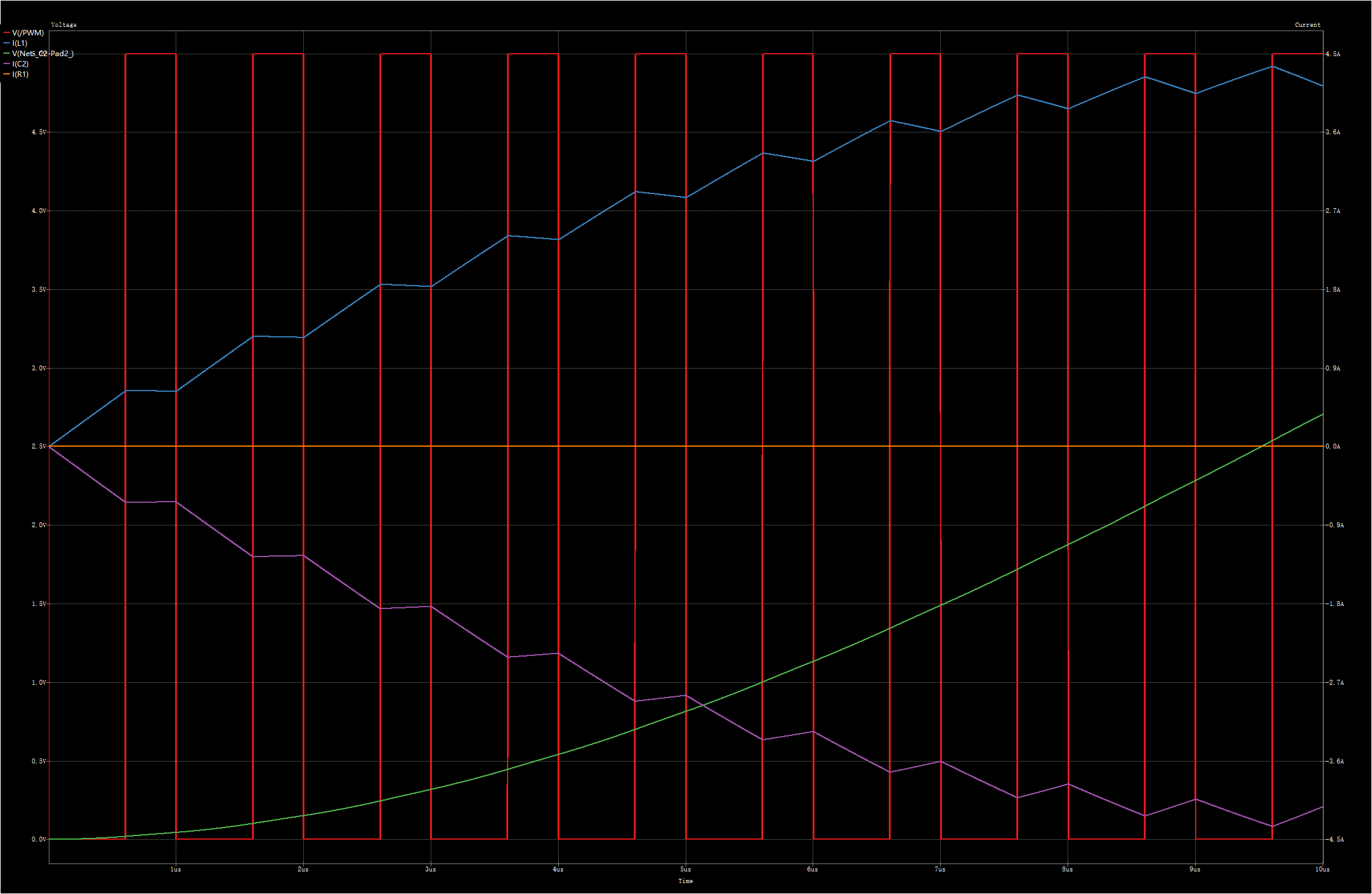
红线是PWM波形,当PWM为低电平时,Q1开启,Q2关闭,电感L1充电,可以看到,随着输出电容C2电压的升高,L1的充电电流在变缓,其斜率为:
k 1 = Δ i Δ t = V C 1 − V C 2 L 1 k_1 = \frac {\Delta i} {\Delta t} = \frac {V_{C1} - V_{C2}} {L1} k1=ΔtΔi=L1VC1−VC2
V C 1 V_{C1} VC1为输入电压,5V,不变; V C 2 V_{C2} VC2为输出电压,在不断上升,所以L1的充电电流斜率在减小。
当PWM为高电平时,Q1关闭,Q2开启,电感L1放电,放电电流斜率为:
k 2 = Δ i Δ t = V C 2 L 1 k_2 = \frac {\Delta i} {\Delta t} = \frac {V_{C2}} {L1} k2=ΔtΔi=L1VC2
所以随着C2电压的升高,电感放电电流斜率在增大。
而在这10个周期中,电感电流几乎都流向C2,给C2充电。
2. 100个周期
把时间增大到100us,即100个周期:
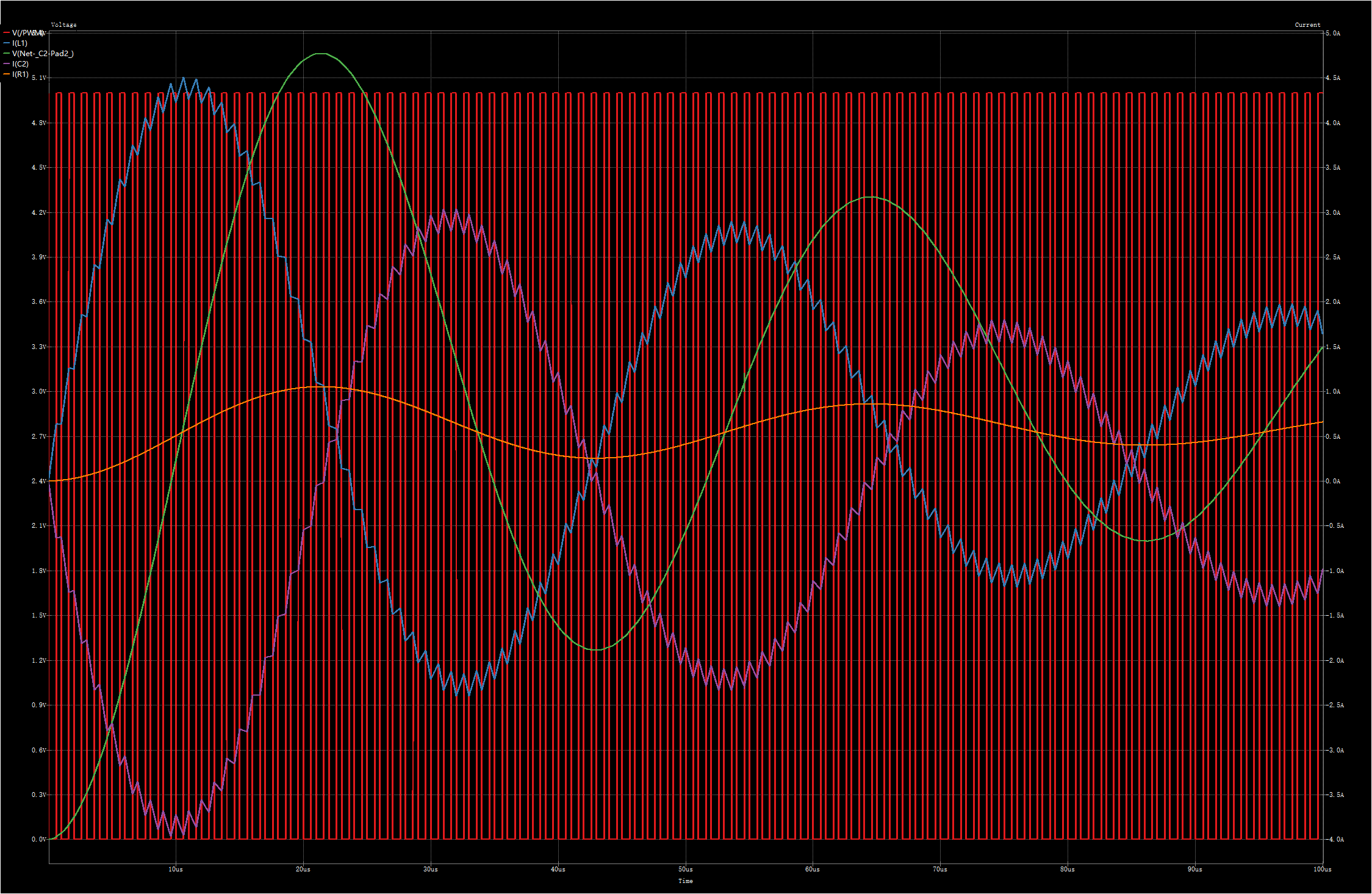
为了让负载电阻的电流更加明显,已经将R1从500Ω变为5Ω。
出现振荡波形了,输出电压在衰减振荡,这主要是因为没有反馈环路进行控制,并且仿真的电路是同步整流,Q2是双向导通的。但是可以看到输出电压和负载电流都是衰减振荡,可以合理想象,仿真时间继续延长,它们一定会趋于一个固定值,达到稳态。
我们先把Q2换成二极管来试一下:
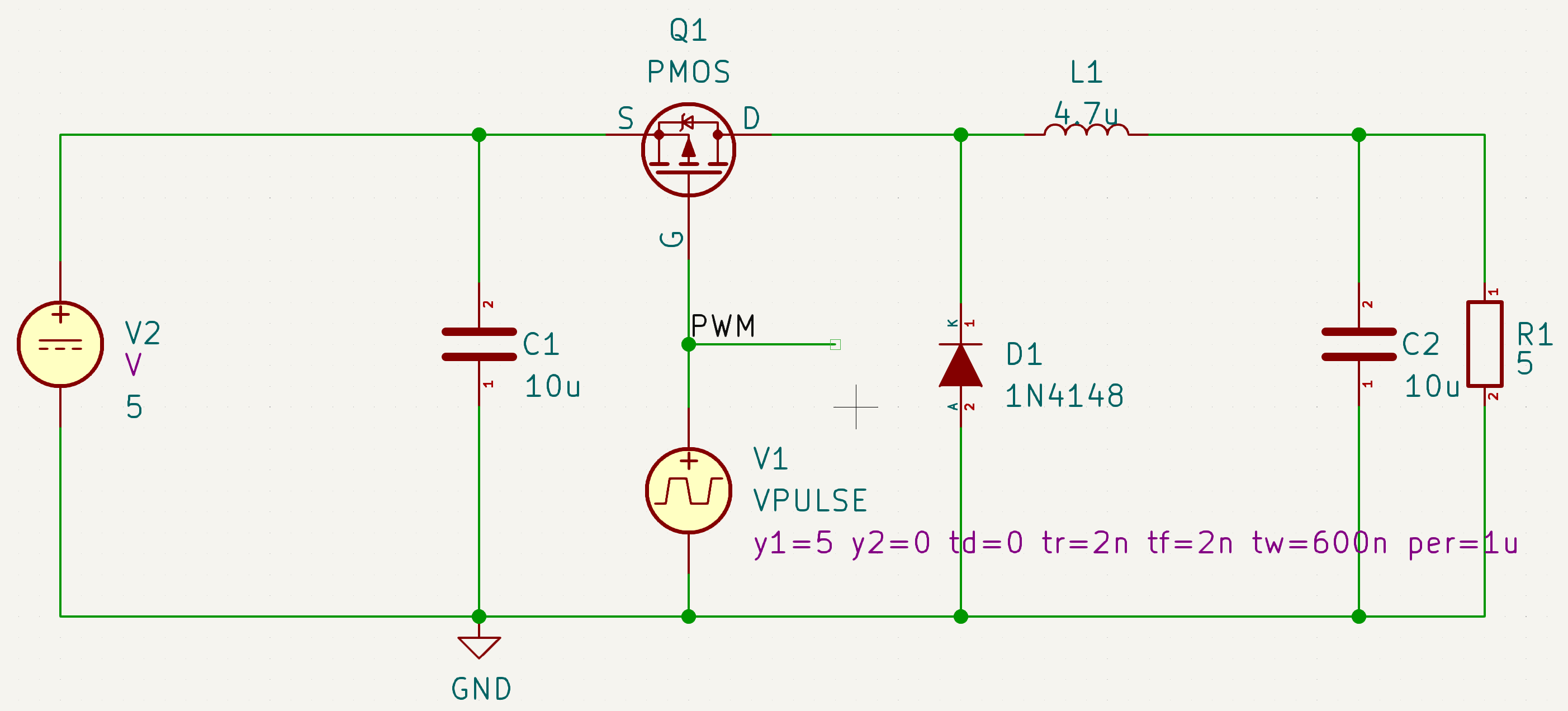

果然不再振荡了,当电感电流降到接近0时,不会再反向,而是再次逐渐充电。
但这不是我们想要的结果,我们继续在前面的原理图上想办法。仿真原理图中,L1是一个近似理想电感,我们可以加一个电阻来增大阻尼:

这样输出电压就会快速收敛。但是这个串联电阻设为1Ω,跟负载电阻的5Ω已经是同一数量级,从仿真结果上也可以看到,这时输出电压趋于2.5V,其实就是5 × 60% × 5 ÷ (1 + 5)= 2.5V。实际上,DCDC 降压芯片基本原理及选型主要参数介绍 这篇文章中的设计实例,使用的电感ESR在150mΩ到200mΩ。
3. 稳态
将电感串联电阻R2设为100mΩ,仿真500us:

差不多在300us,输出电压和负载电流不再变化。我们推导下输出电压和输入电压的关系:
设输入电压为 V i V_i Vi,输出电压为 V o V_o Vo,
当电路达到稳态时:
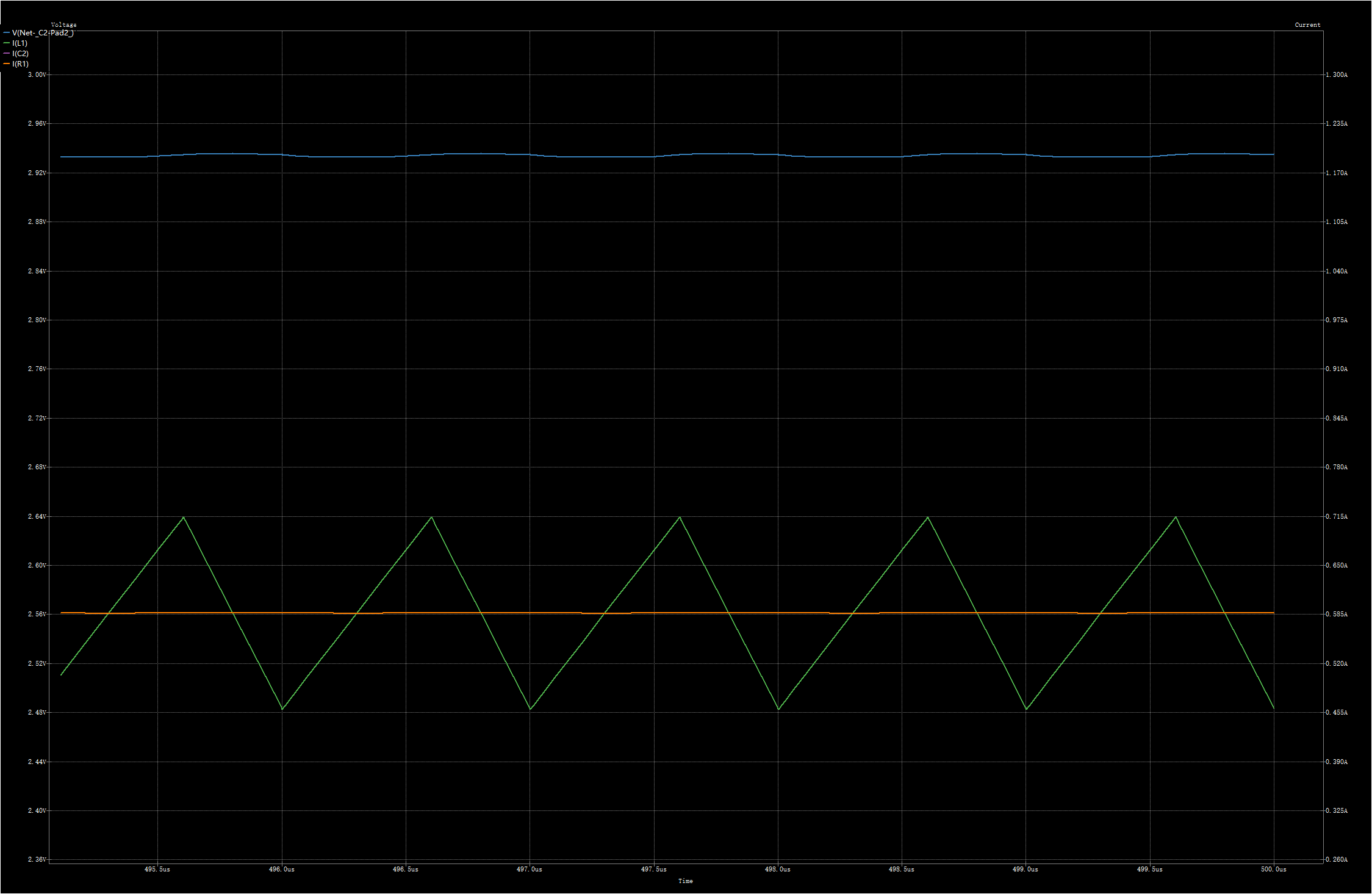
假设电感充放电过程没有损耗,设充电时间为 t 1 t_1 t1,即上图中电感电流上升的时间;放电时间为 t 2 t_2 t2,即上图中电感电流下降时间,则由能量守恒:
∫ 0 t 1 ( V i − V o ) ⋅ i ⋅ d t = ∫ 0 t 2 V o ⋅ i ⋅ d t \int_{0}^{t_1} (V_i - V_o) \cdot i \cdot dt = \int_{0}^{t_2} V_o \cdot i \cdot dt ∫0t1(Vi−Vo)⋅i⋅dt=∫0t2Vo⋅i⋅dt
在稳态时,电感充电平均电流与放电平均电流相等,则有:
( V i − V o ) ⋅ t 1 = V o ⋅ t 2 (V_i - V_o) \cdot t_1 = V_o \cdot t_2 (Vi−Vo)⋅t1=Vo⋅t2
这就是电感的伏秒积守恒,进而可得:
V o = t 1 t 1 + t 2 V i {V_o} = \frac{t_1}{t_1 + t_2} V_i Vo=t1+t2t1Vi
其实从上面的电感电流波形出发,也不难推导出上式。
dcdc降压芯片中,通过给PWM控制器引入反馈实现当输出负载或输入电压变化时能够保持输出电压稳定不变,反馈环路的设计是控制器的核心。
公众号 | FunIO
微信搜一搜 “funio”,发现更多精彩内容。
个人博客 | blog.boringhex.top