主要参考:
时域分析——有量纲特征值含义一网打尽
信号时域分析方法的理解(峰值因子、脉冲因子、裕度因子、峭度因子、波形因子和偏度等)
重要笔记如下:
建议跟参考笔记同步看。
有量纲特征值8个——最大值、最小值、峰峰值、均值、方差、标准差、均方值、均方根值(RMS)
无量纲特征值6个——峭度、偏度、波形因子、峰值因子、脉冲因子、裕度因子
频域特征值5个——重心频率、均方频率、均方根频率、频率方差、频率标准差
谱峭度特征4个——谱峭度的均值、谱峭度的标准差、谱峭度的偏度、谱峭度的峭度
(其他相关特征若干——后续还会补充其他常用、不常用的特征指标)
1,有量纲特征值
- 有量纲特征值:有量纲的特征值往往具有直观的物理含义,是最为常用的特征指标。有量纲特征值主要包括:最大值、最小值、峰峰值、均值、方差、标准差、均方值、均方根值(RMS)、均方误差(MSE)、均方根误差(RMSE)、方根幅值等。
- 均方根代表了信号的能量
- 方差,代表了数据(信号)的离散程度
- 从物理含义上讲,均方值代表信号的能量,期望的平方代表信号的直流分量,而方差代表信号的交流分量。
- 标准差: 方差和标准差都表示数据的离散程度,那么既然有了方差,为什么还要有标准差呢?为了和原始信号统一量纲。
举个例子,假设北京一年的平均气温是20℃,气温标准差是10℃;乌鲁木齐一年的平均气温是20℃,气温标准差是15℃。这样会对气温的离散程度有一个直观理解,但如果说北京的气温方差是100,乌鲁木齐是225,就很不方便理解了。 - 均方误差:
均方误差MSE可以评价数据的变化(偏离)程度,MSE的值越小(相互之间的比较,而不是跟参数真值的比较),说明预测模型描述实验数据具有更好的精确度。
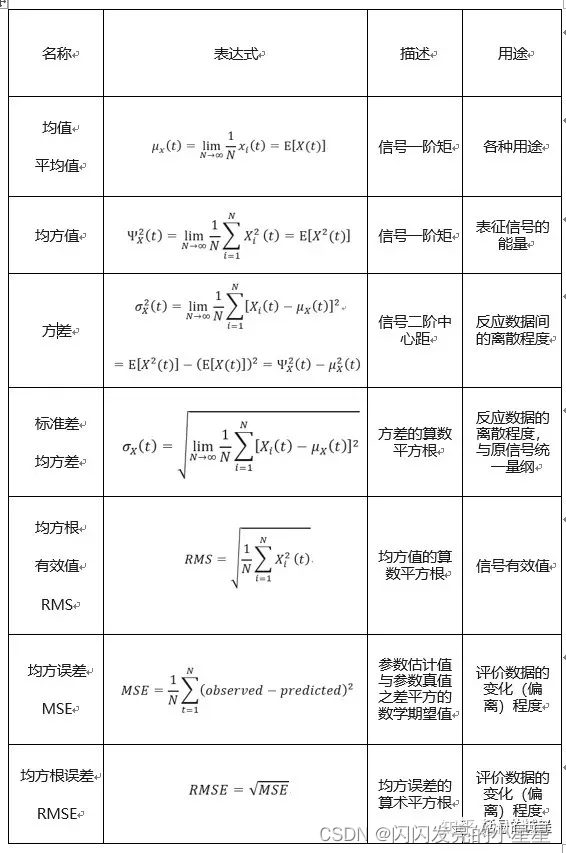
摘自:https://zhuanlan.zhihu.com/p/57153601
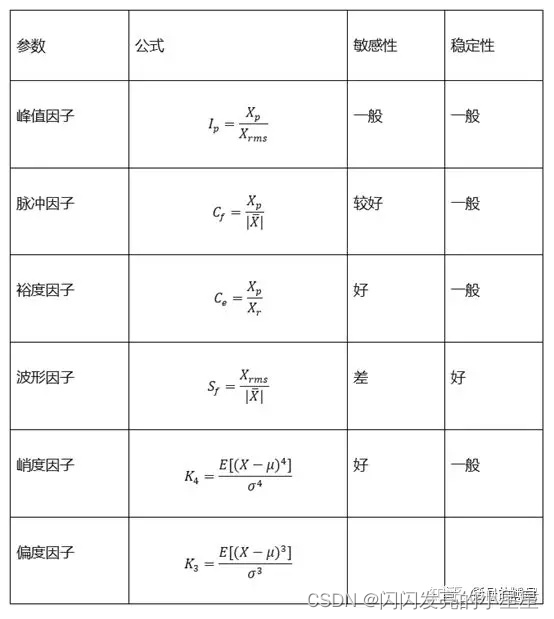
2 无量纲特征
综合来说:峰值因子、脉冲因子和裕度因子的物理意义是相似的,峰值因子和脉冲因子都是用来检测信号中有无冲击的指标,裕度因子常用来检测机械设备的磨损状况。峭度因子也是对振动信号冲击特性的反应,不过公式的表达形式上与前三个差异较大。
偏度:偏度也叫偏斜度、偏态。偏度和峭度是有一定的相关性的,峭度是四阶中心矩和标准差的四次方的比值;偏度是三阶中心矩和标准差的三次方的比值。偏度与峭度相同,描述的是分布。物理含义简单理解的话,对于单峰分布,负偏度代表分布图线的“头”在右侧,“尾”在左侧;正偏度反之。参看下图:
波形因子:波性因子是有效值(RMS)与整流平均值的比值。在电子领域其物理含义可以理解为直流电流相对于等功率的交流电流的比值,其值大于等于1。说到这儿也许你已经发现了,波形因子=脉冲因子/峰值因子。