计算机图形学-GAMES101-6

news2025/1/11 9:57:40

一、前情提要

  • 在观察和投影变换的基础上提出了视口变换，最终我们会将【-1,1】^ 3 立方体转换到屏幕空间中去。
    在这里插入图片描述
  • 当所有图像都在屏幕空间中时，我们就要将所有的图像画在屏幕上，这个过程就是光栅化，光栅化就是简单的在屏幕空间的采样。最重要的思想：我们要用像素的中心，对三角形可见函数进行采样。

二、走样与反走样

（1）问题的提出

 绘制下图中的三角形。
在这里插入图片描述

 检查像素是否在三角形内(进行采样)：
在这里插入图片描述
 根据采样结果进行成像：
在这里插入图片描述
 对比原三角形，成像结果与预期差距很大，并且生成的三角形是有锯齿的。

（2）走样的例子

  • 下图是采样中产生的一种走样在这里插入图片描述

  • 下图是采样中产生的另一种走样：摩尔纹。如下图所示，对坐边原图去掉奇数行和奇数列，再展示同样大小的图像就得到了右边的图像。
    在这里插入图片描述

  • 动画和视频是对图像在时间上的采样，下图为在时间中采样产生的走样。在这里插入图片描述

  • 走样的本质：信号(函数)变换速度太快，导致采样的速度跟不上变换的速度。

（3）反走样的核心思想

 反走样第一步：对原始的图像或信号做一个模糊或滤波
在这里插入图片描述
 直接采样的走样情况：
在这里插入图片描述
 模糊(反走样)后采样的情况：
在这里插入图片描述
 Blurred Aliasing走样后模糊，会导致情况更加糟糕。

三、反走样的本质

（1）从频率上分析走样

  • 频域(Frequency Domain)和频率(Frequency)
    在这里插入图片描述

  • 通过傅里叶变换，我们可以知道：任何周期函数，都可以看作是不同振幅，不同相位正弦波的叠加。因此我们可以将函数变成不同频率的段，并且我们把不同频率的段显示出来。

  • 下图中有五段不同频率的函数，越往下函数的频率越高。
    在这里插入图片描述

  • 我们采取同样的频率对以上五个函数采样结果如下：
    在这里插入图片描述

  • 可以看到到f5时采样效果非常差，这告诉我们采样频率要根据函数本身的频率来决定，如果函数本身频率很高而采样频率很低就会发生走样，无法恢复出原始的信号。

（2）定义走样

  • 走样的定义：对两种频率不同的信号进行采样，根据得到的结果我们无法区分它们。
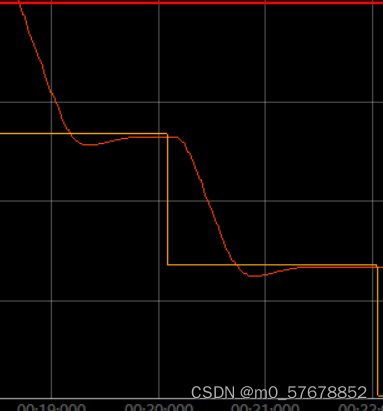
  • 下图中我们可以看到两条曲线，它们分别对应两条原始信号，如果我们使用图中圆圈的点去采样这两条原始信号，会得到相同的采样结果，这就是走样。
    在这里插入图片描述

（3）Filtering滤波

  • 滤波：删除原始信号中频率位于一定区间的波。

  • 通过傅里叶变换得到信号的频域图(频谱)
    在这里插入图片描述

  • 删除频域图中低频的信号，即进行高通滤波(高频通过)，然后再进行逆傅里叶变换将频域图还原回原始的信号，如下图左边所示。下图右边频域图中心变黑就是抹除了低频信号，留下的高频信号属于图像的轮廓(因为轮廓出信息变换的很快)。
    在这里插入图片描述

  • 低通滤波，如下频域图所示，过滤掉所有的高频信号后，再逆傅里叶变换得到的图像如左图所示，保留了内容但是少掉了轮廓：
    在这里插入图片描述

  • 提取频率位于固定区间(不高但也不低)的信息：
    -

（4）滤波-平均-卷积

 做一个卷积操作：
在这里插入图片描述
 可以直接对图像进行卷积操作。也可以先把图像通过傅里叶变换转到频域上，然后把卷积也转到频域上，再相乘再逆傅里叶变换。时域的卷积等于频域的乘积。
在这里插入图片描述

（5）分析采样的本质

 原始信号为a，采样的一些列冲击函数为c，得到的采样结果为e。又因为时域上的乘积等于频域上的卷积，采样就是在重复一个原始信号的频谱，如下图中右边所示采样就是重复复制原始信号的频谱。
在这里插入图片描述
 正常采样与走样如下图所示，如下图圈中所示，走样就是在重复复制原始信号的频谱时导致了重叠。
在这里插入图片描述
 分辨率的提高有利于降低走样的发生。

（6）定义反走样

 经过上面的阐述，我们先对原始信号进行低通滤波，这样我们再进行采样，就不容易发生走样。即先进行模糊，再进行采样，这就是反走样。
在这里插入图片描述
 在实际操作中，我们应该如何模糊一个三角形？我们用一定大小的滤波器对图像进行卷积，达到模糊操作。

（7）MSAA反走样技术

 现在回到三角形，之前我们对于每个像素的采样函数仅判断它是否被覆盖，覆盖了就涂颜色，没覆盖就不涂，而现在我们为了反走样要进行模糊。
 我们根据像素方格被三角形覆盖的面积去决定它的颜色，这样它就不至于要么是涂满颜色的，要么是没有颜色的，这样我们的采样函数就也能涉及一些"像素中心点未覆盖，但像素方格被覆盖"的像素点，以达到模糊三角形边缘区域的目的。
 如果一个像素点被完全覆盖，那么我们就给它100%三角形对应区域的颜色，如果只被覆盖了一般，那就给它50%三角形对应区域的颜色。如下图所示：
在这里插入图片描述
 那么我们如何得到每一个像素方格被三角形覆盖的面积呢？MSAA近似反走样。如下图所示，我们在像素方格中内置更多采样点，通过计算内部采样点的覆盖率去近似计算出 像素方格被三角形覆盖面积的占比。
在这里插入图片描述
 使用MSAA反走样(模糊)的示意图如下：
在这里插入图片描述
 模糊操作完成后得到的信息：
在这里插入图片描述
 MSAA其实隐含了采样，因为上图我们已经可以得到颜色占比，采样是再乘以三角形颜色值即可。

（8）MSAA反走样的代价

 MSAA的代价：增大了计算量，如果使用4×4的采样点，则增大了16倍的计算量。在工业上会用不同的图案去分布采样点，并且一个采样点会被其他像素复用。

（9）其他的抗锯齿方案

 FXAA，原理：后期处理。得到有锯齿的图，找到有锯齿的边界，换成没有锯齿的边界。
 TAA，复用上一帧的颜色值，即把MSAA计算的的颜色分布在了时间商。
 超分辨率：把低分辨率图像转换成高分辨率图像，例如把512×512变成1024×102，要解决的也是采样率不足。但是这些未知的值要去猜，一般使用AI深度学习。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/536265.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

独家公布！985/211高校毕业生源数量统计Top10揭晓……

独家公布！985/211高校毕业生源数量统计Top10揭晓……

2023，985/211高校硕博毕业生总数约达49W。 这是在各大高校官网、官方公众号统计/整理后得到的数据。可能不完全，但数量已经足够庞大，就业竞争也更为激烈。 为了帮助大家更好地了解这些大学的毕业生源情况，本文将为大家揭晓&#x…
阅读更多...
Live800：新消费浪潮涌起，在线客服系统如何“升级”？

Live800：新消费浪潮涌起，在线客服系统如何“升级”？

时代在发展，舞台下的观众已经逐渐成长。 伴随着时代的快速发展，一方面，消费者的行为习惯和消费决策模式变迁，消费者的心理、兴趣及年龄层发生了巨大变化。另一方面，互联网信息透明化打破行业边界，让消费者…
阅读更多...
赛效：如何在线变声改变产品宣传片配音

赛效：如何在线变声改变产品宣传片配音

1：打开网页版腾讯智影并登录账号，点击智能小工具里的“智能变声”。 2：我们页面左侧上传音频。 3：试听变声模板后，选择一个模板，点击右下角“制作变声音频并下载”。 4：变声视频声音生成后&…
阅读更多...
FastDeploy之hello world(C++)

FastDeploy之hello world(C++)

文章目录 环境准备获取模型和测试图像准备CMakeList.txt准备C推理代码编译可执行程序运行可执行程序可能遇到的问题参考 环境准备 CUDA > 11.2cuDNN > 8.0python > 3.6Linux(x64) 下载FastDeploy C SDK wget https://bj.bcebos.com/fastdeploy/release/cpp/fastdep…
阅读更多...
Unity 判断物体是否在阴影中

Unity 判断物体是否在阴影中

文章目录 前言效果视频原理步骤源码总结💢💢版权声明 前言 如题所示，今天接到的需求是：Unity 判断物体是否在阴影中 效果视频 链接：https://www.bilibili.com/video/BV1wc411N7KF/?vd_source75bbe3d71b926e90fdfca6…
阅读更多...
关于argparse和sys.argv的补充

关于argparse和sys.argv的补充

1: sys.argv参考：(10条消息) Python 中 sys.argv 用法详解_ys.journey的博客-CSDN博客 从命令行输入的参数会被保存到sys.argv 2: argparse: 参考：python命令行解析模块argparse用法小结 - 朴素贝叶斯 - 博客园 (cnblogs.com) 除此以外： …
阅读更多...
SpringCloud概述

SpringCloud概述

前言 什么是微服务？ ​ 微服务是一种面向服务的架构(SOA)风格，其中，应用程序被构建为多个不同的小型服务的集合而不是单个应用程序。与单个程序不同的是，微服务让你可以同时运行多个独立的应用程序，而这些独立的应用…
阅读更多...
js文件上传和下载的进度处理

js文件上传和下载的进度处理

发起请求的方式有Axios、XMLHttpRequest、Fetch Axios Axios下载进度演示-onDownloadProgress <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEe…
阅读更多...
【zmq】zguide和cppzmq及windows测试程序

【zmq】zguide和cppzmq及windows测试程序

官方的zguide还是有更新的c++例子zguide构建的工程没更新 官方文档说支持3.2   Updated and revised for ZeroMQ/3.2 (older text for ZeroMQ/2.2 still available).libzmq 本身是c++实现的 我现在的libzmq版本是4.3.4，头文件#include <zmq.hpp>
阅读更多...
STM32开发（十九）STM32F103 数据手册 —— 低功耗模式解析

STM32开发（十九）STM32F103 数据手册 —— 低功耗模式解析

文章目录 低功耗介绍stm32 供电框图低功耗模式睡眠模式停止模式待机模式低功耗模式汇总低功耗介绍 系统复位或上电复位后，微控制器进入运行模式。在运行模式下，CPU通过HCLK提供时钟，并执行程序代码。 系统提供多种低功耗模式，可以在CPU不需要运行时进入低功耗模式节省功耗…
阅读更多...
一看就会的React入门

一看就会的React入门

目录 简介 入门案例 直接创建 函数式创建 类实例创建 组件实例三大核心属性 state 代码演示 props refs 简介 1). Facebook开源的一个js库 2). 一个用来动态构建用户界面的js库 3). React的特点 Declarative(声明式编码) Component-Based(组件化编码) Le…
阅读更多...
生物医学神经网络的方向感

生物医学神经网络的方向感

文章目录 A Sense of Direction in Biomedical Neural Networks摘要本文方法Rotation Mechanism 实验结果 A Sense of Direction in Biomedical Neural Networks 摘要 本文描述了一种使模型不仅知道强度&#xff0c;还知道特征方向和尺度等特性的方法。当分析包含诸如血管或纤…
阅读更多...
PID单环控制（位置环）

PID单环控制（位置环）

今天我们来聊一聊pid如果控制轮子转动位置 前期准备调试过程 前期准备 需要准备的几个条件&#xff1a; 1.获取实时编码器的计数值 2.写好pid控制算法的函数 3.设定好时间多久执行一次pid计算&#xff0c;并设置限幅输出。 4.多久执行一次pid输出 接下来我们看看这几个部分的…
阅读更多...
Vue（ajax、插槽）

Vue（ajax、插槽）

一、ajax请求 1. 实现ajax请求方式&#xff1a; xhr&#xff1a;原生 jquery封装xhr axios&#xff1a;属于promise fetch 2. axios实现步骤&#xff1a; 1.首先安装axios //安装 npm i axios 2. 在本地准备两个服务端 //student const express require(express) const a…
阅读更多...
一级缓存和二级缓存问题

一级缓存和二级缓存问题

介绍 MyBatis 中的缓存&#xff0c;主要分为一级缓存和二级缓存。 一级缓存是 SqlSession 级别的缓存&#xff0c;也叫本地缓存。当执行一个 SqlSession 的查询时&#xff0c;查询到的结果会被保存在 SqlSession 的缓存中。同一个 SqlSession 内执行相同的 SQL 语句&#xff…
阅读更多...
C语言CRC-16 CCITT-FALSE格式校验函数

C语言CRC-16 CCITT-FALSE格式校验函数

C语言CRC-16 CCITT-FALSE格式校验函数 CRC-16校验产生2个字节长度的数据校验码&#xff0c;通过计算得到的校验码和获得的校验码比较&#xff0c;用于验证获得的数据的正确性。基本的CRC-16校验算法实现&#xff0c;参考&#xff1a; C语言标准CRC-16校验函数。 不同应用规范…
阅读更多...
【MySQL】浅谈事务

【MySQL】浅谈事务

哈喽&#xff0c;大家好~我是你们的老朋友&#xff1a;保护小周ღ 谈起 “事务”&#xff0c;可能大家都会在心中出现一个大大的 &#xff1f;&#xff0c;博主的理解——事务就是解决 MySql数据库在应对多线程环境下针对同一存储空间的数据修改引起的数据安全问题的一种机制…
阅读更多...
JMeter入门配置

JMeter入门配置

目录 场景&#xff1a; 环境及工具 &#xff1a; JMeter中文配置&#xff1a; 配置登录接口&#xff1a; 配置响应结果&#xff1a; 配置json提取器 测试json提取器 配置Beanshell后置处理器&#xff1a; http请求右键-->添加---->后置处理器--->Beanshell后置处理…
阅读更多...
pta（浙大第四版）五道经典练习题②

pta（浙大第四版）五道经典练习题②

目录 ①、递归正序输出整数 ②、递归逆序整数并返回 ③、递归实现十进制转二进制 ④、英语单词排序&#xff08;​编辑&#xff09; ⑤、输出月份英文名 ①、递归正序输出整数 题述&#xff1a;给一个正整数n&#xff0c;请利用递归按顺序输出它的每位数&#xff0c;输出一…
阅读更多...
【NovelAI 小说SD批量生成 文生图/视频克隆】环境配置和使用方法

【NovelAI 小说SD批量生成 文生图/视频克隆】环境配置和使用方法

【样品】《谜影之夜》文生图全自动版SD一键成片 操作步骤&环境配置地址&#xff1a; 【NovelAI】月产10000全自动批量原创小说短视频支持文生图和视频克隆 该文章面向购买脚本的付费用户&#xff0c;提供所有问题以及解决办法。使用 notepad 打开对应的文件即可&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023