leecode106 中序遍历和后序遍历构造一棵二叉树
🔎中序遍历和后续遍历的性质
在后序遍历中,最后一个元素二叉树的根节点
在中序遍历序列中,根节点的左边为左子树,右边为右子树
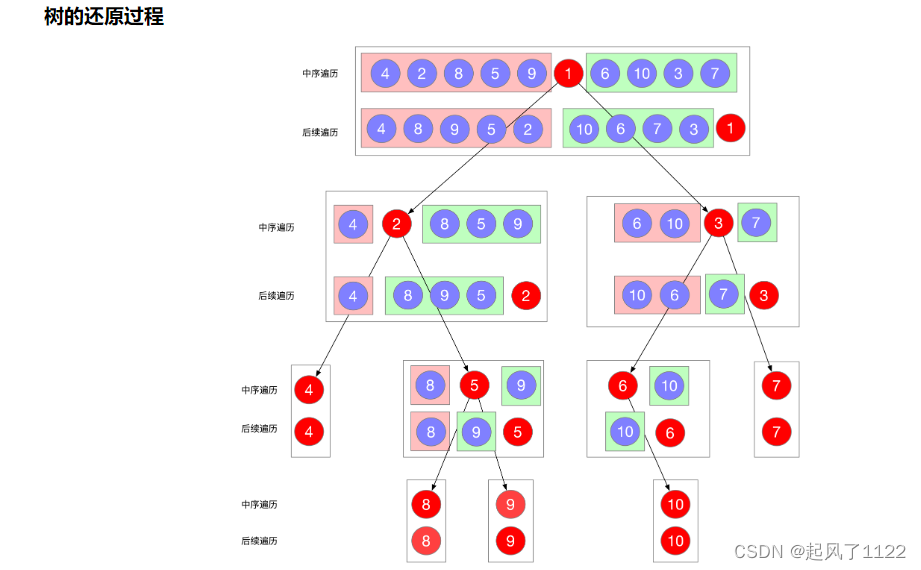
🔎1.二叉树的还原过程描述
1.首先,在后续遍历中找到最后一个元素为根节点
2.根据后续遍历找到中序遍历的根节点位置
3.根据根节点的位置将中序遍历序列分为左子树和右子树
4.根据根节点的位置确定左子树和右子树在中序遍历和后序遍历的位置
5.递归构造左子树和右子树
6.返回根节点结束。
🔎2.二叉树的还原过程变量定义
需要定义以下变量对树进行还原。
1.使用HashMap保存中序遍历的元素和索之间的位置关系。因为在后序遍历找到根节点之后,需要在中序遍历中根据根节点将树划分为左子树和右子树。
2.ri为根节点在中序遍历中的位置
3.中序遍历数组的两个标记位置[is,ie],分别表示起始位置和结束位置
4.后续遍历数组的两个标记位置[ps,pe],分别表示起始位置和结束位置。
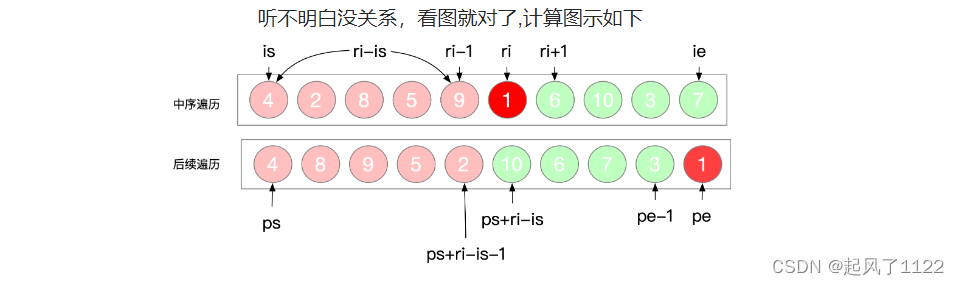
🔎3.位置关系的计算
在找到根节点以后,需要确定下一轮中,左子树和右子树在中序遍历数组和后序遍历数组的左右边界位置。
左子树-中序数组 is = is, ie = ri - 1
左子树-后序数组 ps = ps, pe = ps + ri - is - 1 (pe计算过程解释,后续数组的起始位置加上左子树长度-1 就是后后序数组结束位置了,左子树的长度 = 根节点索引-左子树)
右子树-中序数组 is = ri + 1, ie = ie
右子树-后序数组 ps = ps + ri - is, pe - 1
📖补充:
📒1.怎么利用中序遍历中根节点的位置ri来确定后序遍历中确定左子树的范围?
在中序遍历中,根节点的位置 ri 表示根节点在中序遍历结果数组中的索引位置。由于后序遍历的特性,根节点总是位于后序遍历结果数组的最后一个位置。
要确定左子树在后序遍历结果数组中的范围,我们需要考虑以下几点:
(1)左子树节点在后序遍历结果数组中的相对顺序与中序遍历结果数组中的相对顺序是一致的。也就是说,左子树节点在后序遍历结果数组中出现在根节点之前。
(2)左子树在中序遍历结果数组中的节点个数可以通过 ri - is 来计算,其中 ri 是根节点的位置,is 是当前子树在中序遍历结果数组中的起始位置。
(3)根据左子树在中序遍历结果数组中的节点个数,我们可以推断出左子树在后序遍历结果数组中的范围。左子树在后序遍历结果数组中的起始位置为 ps,即当前子树在后序遍历结果数组中的起始位置。左子树在后序遍历结果数组中的结束位置为 ps + ri - is - 1,即左子树的节点个数减1加上起始位置。
📒2.中序遍历和后序遍历的性质?
(1)中序遍历:左子树的节点总在根节点的左侧,右子树的节点总在根节点的右侧
(2)后序遍历:根节点总是在最后一个位置,而左子树的节点总是出现在右子树之前。
(3)假设我们已经知道左子树在中序遍历结果数组中的节点个数为leftcount,而后序遍历结果数组范围为[ps,pe],ps为起始索引,pe为结束索引。
(4)根据后序遍历的特点,根节点总是在最后一个位置,即post[pe]是根节点的值。中序遍历的根节点为memo.get(root)
(5)那我们可以得到以下关系:
a:左子树在后序遍历结果数组中的节点个数为 leftCount,因此右子树在后序遍历结果数组中的节点个数为 pe - ps - leftCount。
b:左子树在中序遍历结果数组中的范围为 [is, ri - 1],其中 is 是左子树在中序遍历结果数组中的起始索引,ri - 1 是左子树在中序遍历结果数组中的结束索引。左子树在后序遍历结果数组中的范围为 [ps, ps + leftCount - 1]。
c:右子树在中序遍历结果数组中的范围为 [ri + 1, ie],其中 ri + 1 是右子树在中序遍历结果数组中的起始索引,ie 是右子树在中序遍历结果数组中的结束索引。
d:右子树在后序遍历结果数组中的范围为 [ps + leftCount, pe - 1]
3.为什么使用HashMap?
HashMap是一种常用的数据结构,用于存储键值对。在算法和编程中,使用HashMap可以提供高效的数据查找和检索操作。
在给定的代码示例中,使用HashMap的目的是为了快速查找中序遍历中每个节点的位置。这样做是为了在后序遍历中找到当前子树的根节点的位置,进而划分出左子树和右子树的范围。HashMap的键表示节点的值,值表示节点在中序遍历数组中的索引位置。通过构建这个HashMap,在查找根节点的位置时,可以在常数时间内找到对应的索引。
使用HashMap的好处是可以在常数时间内进行查找操作,因此可以提高程序的运行效率。它可以用于解决需要频繁查找、索引或映射的问题,例如查找元素、统计元素出现次数、快速访问数据等。
代码如下:
class Solution {
HashMap<Integer,Integer> memo = new HashMap<>();
int[] post;
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i = 0;i < inorder.length; i++) memo.put(inorder[i], i);
post = postorder;
TreeNode root = buildTree(0, inorder.length - 1, 0, post.length - 1);
return root;
}
public TreeNode buildTree(int is, int ie, int ps, int pe) {
if(ie < is || pe < ps) return null;
int root = post[pe];
int ri = memo.get(root);
TreeNode node = new TreeNode(root);
node.left = buildTree(is, ri - 1, ps, ps + ri - is - 1);
node.right = buildTree(ri + 1, ie, ps + ri - is, pe - 1);
return node;
}
}