006. 分割回文串

news2024/11/24 8:30:12

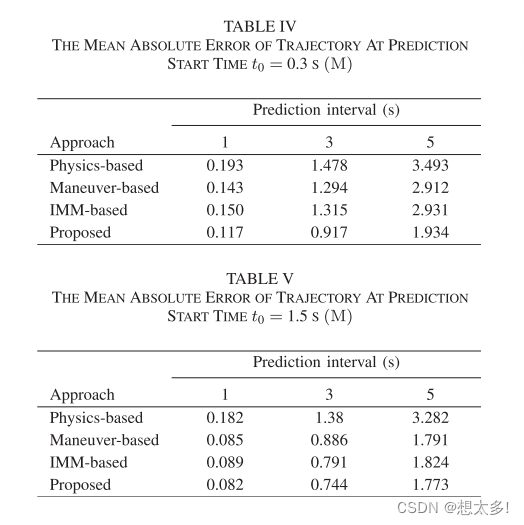
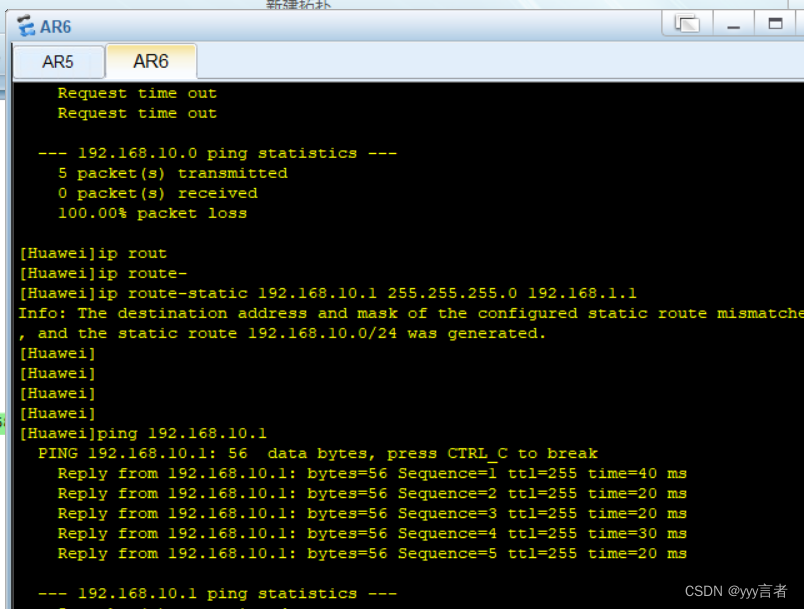
1.题目链接：

131. 分割回文串

2.解题思路：

2.1.题目要求：

给一个字符串 s ，要求把 s 分割成一些子串，并使每个子串都是 回文串。

回文串的概念：正反顺序都一样的字符串。

举例：

输入：s = "aab"

输出：[["a","a","b"],["aa","b"]]

2.2.思路：

for+递归构成 n叉树，用于查找每一份字串组合，再补充判断是不是回文串的逻辑，以及终止条件的确认

n叉树如下：

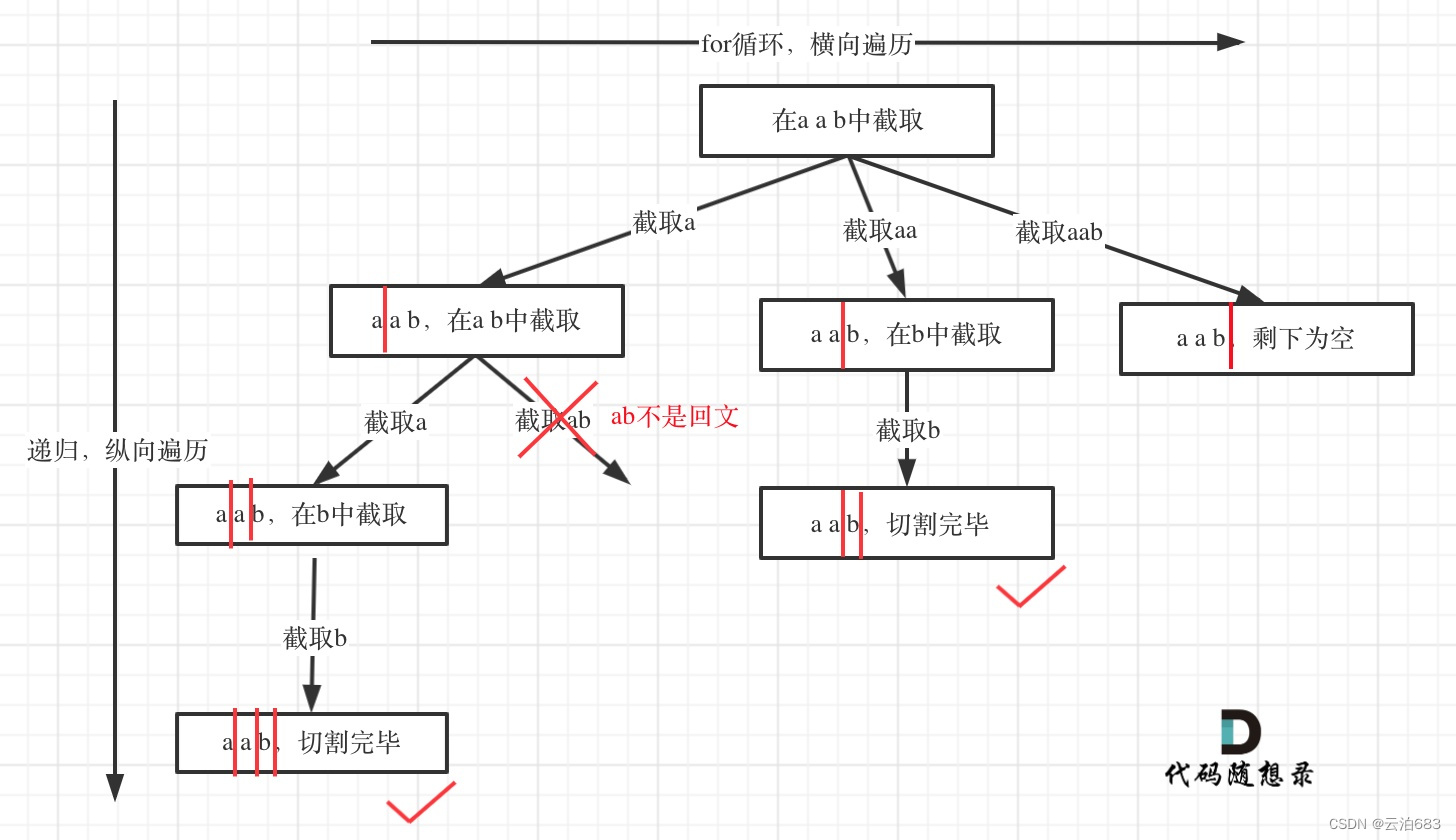
2.3.回溯三部曲：

2.3.1.确定回溯函数参数

path存储一条分割方案的字符串，result是字符串结果集。

参数默认输入 s ，startIndex 用于避免重复切割和切割过程中字串范围确定。

vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex) {

2.3.2.确定终止条件

当切割完最后一个字符串字符的时候，说明已经找到了一组分割方案了，返回到结果集里。

那什么是作为切割完最后一个字符的判断条件？

startIndex >= s.size( ) ，因为 startIndex 在单层遍历逻辑里，记录每次递归的起始位置，到最下面一层的递归时，startIndex 默认是等于 s.size( ) 就停止了的，但大于的情况是怎么产生的？我的理解是 xxxxxx

void backtracking (const string& s, int startIndex) {
    // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
    if (startIndex >= s.size()) {
        result.push_back(path);
        return;
    }
}

2.3.3.确定单层遍历逻辑

这里搜集不同的分割方案，以及判断当下递归的for搜集的每一段字符串是不是符合回文串的定义，不符合就跳过并继续循环。

判断回文子串的范围是如何确定的？

因为每一次递归，搜集指针 i 都从 startIndex 的位置出发（startIndex每次递归都会更新）然后 i 向后遍历，直到末尾，在这个情况下 不断更新的 i 和在非递归的情况下不动的 startIndex 的位置形成的范围，就可以不断判断是不是回文串了，是就搜集，不是就跳过

for (int i = startIndex; i < s.size(); i++) {
    if (isPalindrome(s, startIndex, i)) { // 是回文子串
        // 获取[startIndex,i]在s中的子串
        string str = s.substr(startIndex, i - startIndex + 1);
        path.push_back(str);
    } else {                // 如果不是则直接跳过
        continue;
    }
    backtracking(s, i + 1); // 寻找i+1为起始位置的子串
    path.pop_back();        // 回溯过程，弹出本次已经填在的子串
}

判断回文子串的函数 isPalindrome 用的是双指针法

代码如下：

bool isPalindrome(const string& s, int start, int end) {
     for (int i = start, j = end; i < j; i++, j--) {
         if (s[i] != s[j]) {
             return false;
         }
     }
     return true;
 }

2.4.总代码：

class Solution {
private:
    vector<vector<string>> result;
    vector<string> path; // 放已经回文的子串
    void backtracking (const string& s, int startIndex) {
        // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
        if (startIndex >= s.size()) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindrome(s, startIndex, i)) {   // 是回文子串
                // 获取[startIndex,i]在s中的子串
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            } else {                                // 不是回文，跳过
                continue;
            }
            backtracking(s, i + 1); // 寻找i+1为起始位置的子串
            path.pop_back(); // 回溯过程，弹出本次已经填在的子串
        }
    }
    bool isPalindrome(const string& s, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            if (s[i] != s[j]) {
                return false;
            }
        }
        return true;
    }
public:
    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        backtracking(s, 0);
        return result;
    }
};