数学原理

高斯消元法求行列式：利用初等行变换，化为上三角行列式，求其主对角线的乘积

行列式的初等行变换：

1）换行变换：交换两行（行列式需变号）

2）倍法变换：将行列式的某一行（列）的所有元素同乘以数k（行列式需乘K倍）

3）消法变换：把行列式的某一行（列）的所有元素乘以一个数k并加到另一行（列）的对应元素上（行列式不变）

上述三种变化中，本章只利用第三个消法变换。

例如：

行列式A为：

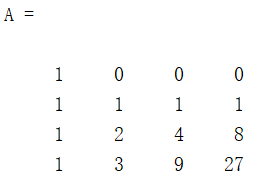
化为上三角行列式：

注：这里的-0.0667是打印时保留四位的结果，其实是-0.066...6667，-3.6667亦然（因为浮点数在计算机中存储的特性，高斯消元法也会损失一点点精度）。

行列式是值为：

det（A）=15 × -0.0666666667 × -6 × 2 =12

程序设计

整体流程与代码

1）判断传入指针是否为空

2）判断矩阵维数，判断是否为方阵

3）为临时矩阵开辟空间

4）将原矩阵数据拷贝到临时矩阵中（保护原矩阵）

5）利用初等行变换，找出每列绝对值最大的数，将该行加到其他行上（1.提高一定的精度 2.避免原函数主对角线有0，需要换行的情况）

6）逐列开始，进行消0操作

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>

double Det(double** src)
{
	//step 1
	//判断指针是否为空
	if (src == NULL)exit(-1);
	int i, j, k, row, col;
	double sum,** res;
	int count = 0;
	//判断矩阵维数
	row = (double)_msize(src) / (double)sizeof(double*);
	col = (double)_msize(*src) / (double)sizeof(double);
	if (row != col)exit(-1);
	//step 2
	res = (double**)malloc(sizeof(double*) * row);
	for (i = 0; i < row; i++)
	{
		res[i] = (double*)malloc(sizeof(double) * row);
		memset(res[i], 0, sizeof(res[0][0]) * row);//初始化
	}
	//step 3
	//进行数据拷贝
	for (i = 0; i < row; i++)
	{
		memcpy(res[i], src[i], sizeof(res[0][0]) * row);
	}
	//step 4
	//每列元素找出最大那一行，加到其他行
	for (j = 0; j < col; j++)
	{
		count = 0;
		double Max = fabs(res[count][j]);//用绝对值比较
		//默认第一行的数最大
		for (i = 0; i < row; i++)
		{
			if (fabs(res[i][j]) > Max)
			{
				count = i;
				Max = fabs(res[i][j]);
			}
		}
		for (i = 0; i < row; i++)
		{
			if (i == count)continue;
			for (k = 0; k < col; k++)
			{
				res[i][k] += res[count][k];
			}
		}
	}
	//step 5
	for (j = 0; j < col; j++)
	{
		//将每列其他元素化0
		for (i = j+1; i < row; i++)
		{
			double b = res[i][j] / res[j][j];
			for (k = 0; k < col; k++)
			{
				res[i][k] += b * res[j][k] * (-1);//初等行变换
			}
		}
	}
	sum = 1;
	for (i = 0; i < row; i++)
	{
		for (j = 0; j < col; j++)
		{
			if (i == j)
				sum *= res[i][j];
		}
	}
	//必须释放res内存！
	free(res);
	return sum;
}

上述代码中：

malloc函数在动态内存规划一文中有详细讲解
判断矩阵维数在C语言判断矩阵维数中有详细讲解
行列式必须是方阵，因此row和col是相等的，代码中row对应行操作，col对应列操作
因为高斯消元法是化为上三角行列式，所以每次消元时，起始的行数i=j+1，上三角部分不用消0
最后只需要返回三角行列式主对角元素的乘积即可，在函数末尾需要释放内存

测试函数

为了方便测试，创建三个测试函数

创建矩阵函数：

double** MakeMat(int n)
{
	int i = 0;
	if (n <= 0)exit(-1);
	double** res = (double**)malloc(sizeof(double*) * n);
	if (res == NULL)exit(-1);
	for (i = 0; i < n; i++)
	{
		res[i] = (double*)malloc(sizeof(double) * n);
	}
	return res;
}

初始化函数：

void InitMat(double** src)
{
	if (src == NULL)exit(-1);
	int i, j, n;
	n = (double)_msize(src) / (double)sizeof(double*);
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			src[i][j] = pow(i, j);
		}
	}
}

初始化为i的j次方

打印函数：

void print(double** src)
{
	if (src == NULL)exit(-1);
	putchar('\n');
	int i, j, row, col;
	row = (double)_msize(src) / (double)sizeof(double*);
	col = (double)_msize(*src) / (double)sizeof(double);
	for (i = 0; i < row; i++)
	{
		for (j = 0; j < col; j++)
		{
			printf("%9.4lf", src[i][j]);
		}
		putchar('\n');
	}
}

测试结果

int main()
{
	int n = 4;
	double** arr = MakeMat(n);
	InitMat(arr);
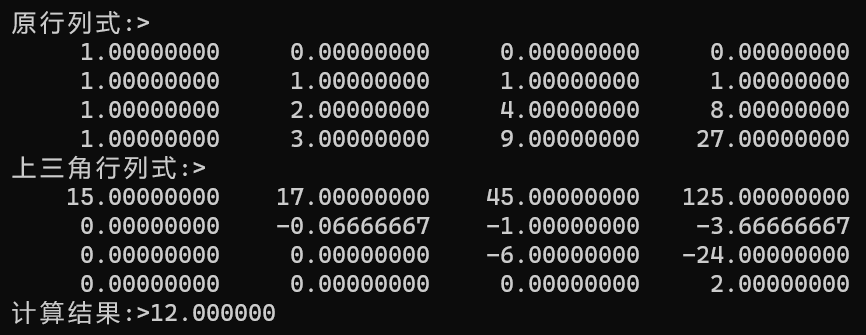
	printf("原行列式:>");
	print(arr);
	printf("上三角行列式:>");
	double res = Det(arr);
	printf("计算结果:>");
	printf("%lf\n", res);
	return 0;
}

这里没有返回上三角行列式，只是在函数最后加了一个打印，对其进行观察