量化投资 无套利 No-arbitrage

State of Nature

经济主体所面临的不确定性是关于在状态空间 $\Omega$ 中对自然状态的实现：

① Ω = { ω 1 ,   ω 2 .   ⋯   ,   ω S } \Omega=\{\omega_1,\,\omega_2.\,\cdots,\,\omega_S\} Ω={ω1​,ω2​.⋯,ωS​} 是全体的状态空间；

② T = { 0 ,   ⋯   ,   T } \bold{T}=\{0,\,\cdots,\,T\} T={0,⋯,T} 代表交易时间；

③ ${\mathbf{F}}_t$ 代表时刻 $t$ 的信息：对于每一个状态 $\omega$ ，${\mathbf{F}}_t(\omega )$ 代表当 $t$ 时刻的状态为 $\omega$ 时，我们所得到的所有信息（或者说剩下的无法排除的状态）。我们假设：
$${\mathbf{F}}_0(\omega )=\Omega ,{\mathbf{F}}_t(\omega )\subseteq {\mathbf{F}}_s(\omega )\text{for}s\le t$$
④ $\mathbf{P}$ 是状态空间上的概率测度。

市场域 Market Span

我们有 $J$ 支可交易证券，他们分别由他们的未来现金流所定义，并且 adapt to 事件空间 $(\Omega ,{\mathbf{F}}_t,\mathbf{P})$ 。（这句话我不知道怎么翻译，可以看一下原文：）

Securities are identified respectively with their future cash flows adapted to the event space $(\Omega ,{\mathbf{F}}_t,\mathbf{P})$

（老师上课强调了 adapt to 和其他措辞的区别，但是我没有听懂。。。）

① 现金流（红利）dividend： { δ t } t = 1 T \{ \delta_t\}_{t=1}^{T} {δt​}t=1T​ ，其中 ${\delta }_t\equiv \left[{\delta }_t^1,\cdots ,{\delta }_t^J\right]$ ，${\delta }_t^j$ 是证券 $j$ 在时刻 $t$ 的现金流；

② 证券价格 Security prices： { p t } t = 0 T \{p_t\}_{t=0}^{T} {pt​}t=0T​ ，$p_t\equiv \left[p_t^1,\cdots ,p_t^J\right]$

③ 交易策略 Trading strategy： { θ t } t = 0 T \{ \theta_t \}_{t=0}^{T} {θt​}t=0T​ ，${\theta }_t=\left[{\theta }_t^1,\cdots ,{\theta }_t^J\right]$ 是时刻 $t$ 的投资组合（注意这里 $\theta$ 并不是投资比例，而是持有量）

④ 现金流 Cash flows：交易策略 $\theta$ 产生的现金流为：（不考虑交易摩擦等）
$$\begin{array}{rl}{d}_t^{\theta }=& {\theta }_{t-1}\cdot (p_t+{\delta }_t)-{\theta }_t\cdot p_t\\ d_0^{\theta }=& -{\theta }_0\cdot p_0\end{array}$$

• $d_t^{\theta }$ 右边可以看成两项：第一项是按照旧的投资组合，此时得到的红利 ${\delta }_t$ ，加上按照这一时刻 $t$ 的价格 $p_t$ 平仓的现金流；第二项是按照新的投资组合的初始投资；
• $d_0^{\theta }$ 就是初始的投资；

⑤ 市场域 Market Span：$\mathbf{D}$ 代表通过所有不同交易策略能够产生的现金流串，称为市场域。市场域构成了一个向量空间，受到参与交易的证券数量约束，$J$ 越大则 $\mathbf{D}$ 一定不会更小，因此 $\mathbf{D}$ 不一定是个完备空间。
D ( p ,   δ ) = { { d t } t = 0 T :    ∃   θ    s . t .    d t θ = d t ,    ∀   t } \bold{D}(p,\,\delta)=\left\{ \{d_t\}_{t=0}^{T}:\,\,\exist\,\theta\,\,s.t.\,\,d_t^{\theta}=d_t,\,\,\forall\, t \right\} D(p,δ)={{dt​}t=0T​:∃θs.t.dtθ​=dt​,∀t}
⑥ 未来市场域 Furure Market Span：理论上可能存在的、除去 0 时刻现金流的现金流串所构成的市场域：
M ( p ,   δ ) = { d − 0 :    d = ( d 0 ,   d − 0 ) ∈ D ( p ,   δ ) } \bold{M}(p,\,\delta)=\left\{ d_{-0}:\,\,d=(d_0,\,d_{-0})\in \bold{D}(p,\,\delta) \right\} M(p,δ)={d−0​:d=(d0​,d−0​)∈D(p,δ)}

套利 Arbitrage

无套利和正线性定价规则 No-arbitrage and Positive Linear Pricing Rule

以下分别介绍无套利的定义以及正线性定价规则，并且将证明二者是等价的。

Definition M3：称交易策略 $\theta$ 是套利的，当 $d_t^{\theta }>0,\forall t\ge 0$ ；

• 理想的市场不应当存在套利机会；
• 套利说明可以做到任何时刻（包括 0 时刻）都是正的现金流，即不需要任何付出就可以“空手套白狼”；

Condition S1：无套利时，存在至少一个正的状态价格过程（state price process） ψ ≡ { ψ t } t ≥ 1 \psi\equiv \{\psi_t\}_{t\geq 1} ψ≡{ψt​}t≥1​ ，使得对于所有的可交易证券，他们当前市场价都可以表示成：
$$\begin{array}{rl}{p}_0^j=& \sum _{t\ge 1}{\psi }_t\cdot {\delta }_t^j\equiv \psi \circ {\delta }^j\\ j=& 1,\cdots ,J\end{array}$$

• 其中 $\cdot$ 分别为随机变量定义的内积，例如 $x\cdot y=\sum _{\omega \in \Omega }x(\omega )y(\omega )$ ；
• ${\psi }_t(\omega )$ 可以看作 $t$ 时刻 $\omega$ 状态下的贴现因子；

Theorem 2：对于有限经济，无套利(M3)与线性定价规则(S1)的存在性是等价的。

证明：$S1\Rightarrow M3$ 是显然的（我也不知道为什么显然。。。），我们接下来证明 $M3\Rightarrow S1$ ：

$M3$ 代表不存在套利时，$\mathbf{D}\cap {\mathbf{R}}_{+}^{m+1}=0$ （这里 $0$ 代表原点，因为没有全为正的现金流，所以跟第一象限只相交于原点），说明原点在 $\mathbf{D}$ 的边界上。而 $\mathbf{D}$ 显然是一个凸集（线性组合可以看成是投资组合的线性组合）。根据 Minkovsky 超平面分离定理，存在一个非零向量 $q\in {\mathbf{R}}^{m+1}$ 使得：
$$q\circ c\ge q\circ d,\forall c\in {\mathbf{R}}_{+}^{m+1},d\in \mathbf{D}$$
取等时，当且仅当 $c=d=0$ ；

• 由于 $c$ 在第一象限，我们取 $c=0$ ，为了满足 $0\ge q\circ d$ 和 $0\ge q\circ -d$ ，我们可以推出 $q\circ d=0$ （$-d$ 相当于将策略取反，所以现金流也相反，因此这个现金流串也是可以得到的，也在 $\mathbf{D}$ 中）；也就是说，对任意 $d\in \mathbf{D}$ ，这个 $q$ 都可以使得 $q\circ d=0$ ；
• 当 $q\circ c>0$ 时，由于 $c\ne 0$ ，而且 $c$ 是在第一象限任意取的，因此 $q$ 的每一维都大于 0，即 $q\gg 0$ ；

第一个关于 $q$ 的条件，我们可以得到：
$$\begin{array}{rl}\sum _{t=0}^T\sum _{\omega \in \Omega }{q}_t(\omega )d_t(\omega )& =0\\ \sum _{\omega \in \Omega }{q}_0(\omega )d_0(\omega )+\sum _{t=1}^T\sum _{\omega \in \Omega }{q}_t(\omega )d_t(\omega )& =0\end{array}$$
我们令 ${\psi }_t(\omega )=\frac{q_t(\omega )}{q_0}>0$ ，因此对于任意 $(d_0,d_{-0})\in \mathbf{D}$ ，有：
$$-d_0=\psi \circ d_{-0}=\sum _{t=1}^T\sum _{\omega \in \Omega }{\psi }_t(\omega )d_t(\omega )$$
（我这边向量维数有点搞懵了。。。）

特别地，对于证券 $j$ ，有：
$$p_0^j=\psi \circ {\delta }^j,j=1,\cdots ,J$$
可以理解成：投资的第一步往往就是按照投资策略买入或卖出某组初始资产，所以 $-d_0$ 就可以看作是价格啦

来看个例题吧（

Exercise 1：考虑一个只有两期、三种状态 { 1 ,   2 ,   3 } \{1,\,2,\,3\} {1,2,3} 的经济体。市场上有两支可交易证券，带来的可能收益为：
$$\begin{array}{rl}{d}^1=& [110,110,110]\\ d^2=& [50,100,150]\end{array}$$
初始价格为 $p^1=p^2=100$ ，判断该市场上是否存在套利机会。

解：由于只有两期，可以理解为，第一期买进的话，第二期就要卖出，或者第一期卖出，第二期就要买进。例如，第一期买入一手 $p^1$ ，第二期卖出，就可以得到 10 元收益。

第一支证券在未来的任意状态下价格都会上涨 10%，可以认为是无风险利率，比如存银行。

要判断是否存在套利机会，按照上面的定理，我们可以判断是否能找到一个严格为正的状态价格过程，使得当前的价格能由未来的现金流来表示。设状态价格过程为 $[{\psi }_1,{\psi }_2,{\psi }_3{]}^T$ ，则：

$$\{\begin{array}{l}110{\psi }_1+110{\psi }_2+110{\psi }_3=100\\ 50{\psi }_1+100{\psi }_2+150{\psi }_3=100\end{array}\Rightarrow \left[\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\end{array}\right]=\left[\begin{array}{c}-\frac{2}{11}\\ \frac{2}{11}\\ 0\end{array}\right]+{\psi }_3\left[\begin{array}{c}1\\ -2\\ 1\end{array}\right]$$

当 ${\psi }_3\in (\frac{2}{11},\frac{6}{11})$ 时，${\psi }_1$ 、${\psi }_2$ 和 ${\psi }_3$ 都大于 0，因此不存在套利机会。

可以看出，第二支证券当前定价为 100 还是合理的。那么，如果 $p^2=150$ ，显然价格是扭曲的，我们可以算一下状态价格过程：
$$\{\begin{array}{l}110{\psi }_1+110{\psi }_2+110{\psi }_3=100\\ 50{\psi }_1+100{\psi }_2+150{\psi }_3=150\end{array}\Rightarrow \left[\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\end{array}\right]=\left[\begin{array}{c}-\frac{13}{11}\\ \frac{10}{11}\\ 0\end{array}\right]+{\psi }_3\left[\begin{array}{c}1\\ -2\\ 1\end{array}\right]$$

可以发现 ${\psi }_1$ 和 ${\psi }_2$ 无法同时大于 0，因此存在套利机会。我们可以看到 $p^2$ 很可能会跌，因此我们可以做空 $2$ ，并且向银行存钱：$d_0=-\frac{15}{11}\times 100+150>0$ ，则在 1 时刻，不论是那种状态下：
$$d_1=\{\begin{array}{l}\frac{15}{11}\times 110-50=100>0\\ \frac{15}{11}\times 110-100=50>0\\ \frac{15}{11}\times 110-100=0\end{array}$$
也就是说不论什么情况下都可以赚钱（

接下来介绍无套利的七个性质：

Implication 1: One-price Principle

一价性：产生两个相同未来现金流的投资组合，一定在当前市场中具有相同支出。因为状态价格过程是未知的，但是实际存在且唯一的。因此对于 $d\in \mathbf{D}$ ，对于任意能够产生 $d$ 的投资策略 $\varphi$ ，它们初始的现金流都是一致的，都是：
$${\Psi }_0(d)\equiv \psi \circ d_{-0}\text{for all}\in \mathbf{D}$$
一价性说明每个未来现金流都对应现在某个价格，这个映射可以表示为价格函数 ${\Psi }_0$ ，价格函数是 well define 的。

Implication 2: Positivity

正性：对于任意非负未来现金流 $d\in \mathbf{D}$ ，都有 ${\Psi }_0(d)\ge 0$：

• 当 $d_{-0}=0$ ， ${\Psi }_0(d)=0$ ，即什么都不做；
• 当 $d_{-0}>0$ ， ${\Psi }_0(d)>0$ ，即要赚到钱，不可能什么都不做；

Implication 3: Additivity

可加性：对于任意 $d^{\prime }$ ，$d^{\prime \prime }\in \mathbf{D}$ ，有 $d^{\prime }+d^{\prime \prime }\in \mathbf{D}$ ，特别地：
$${\Psi }_0(d^{\prime }+d^{\prime \prime })={\Psi }_0(d^{\prime })+{\Psi }_0(d^{\prime \prime })$$
这说明，两个投资组合的总投入，等同于要达到两个投资组合的未来现金流之和得到的新的未来现金流所需要的投入。

Implication 4: Homogeneity

齐次性：对于任意 $d\in \mathbf{D}$ ，以及实数 $\alpha$ ，有：${\Psi }_0(\alpha d)=\alpha {\Psi }_0(d)$

相当于把原来的持有量翻 $\alpha$ 倍。

Implication 1-4 可以证明得到价格函数 ${\Psi }_0(d)$ 是一个正比例函数。

Implication 5: Recursivity

递归性：对于任意 $d\in \mathbf{D}$ ，0 时刻的价格 ${\Psi }_0(d)$ 为：
$${\Psi }_0(d)=\sum _{t\ge 1}{\psi }_t\cdot d_t$$
并且，${\Psi }_0(d)$ 还可以表示为未来第一期现金流加上未来第一期价格 ${\Psi }_1(d)$ 的贴现值，即：
$${\Psi }_0(d)={\psi }_1\cdot [d_1+{\Psi }_1(d)]$$

• 其中 $\cdot$ 分别为随机变量定义的内积，例如 $x\cdot y=\sum _{\omega \in \Omega }x(\omega )y(\omega )$ ；

这相当于得到了一个倒向差分方程。

Implication 6: Risk-neutral Pricing Rule

风险中性定价规则：在事件空间 $(\Omega ,\mathcal{F})$ 上定义概率测度 $\mathbf{Q}$ ，使得对于事件 $A$ ，有：
$$\mathbf{Q}(A)\equiv \frac{\sum _{\omega \in A}{\psi }_1(\omega )}{\sum _{\omega \in \Omega }{\psi }_1(\omega )}$$
测度 $\mathbf{Q}$ 被称为风险中性概率测度。

考虑一个无风险的、收益率为 $R_0^f=1+r_0$ 的一期的贴现债券，由递归性可得：
$$\frac{1}{1+r_0}=\sum _{\omega \in \Omega }{\psi }_1(\omega )$$
（因为无风险，所以所有状态下 $d(\omega )$ 都相等；又因为只有一期，所以把 $d_1+{\Psi }_1(d)$ 除到左边去，得到 $\frac{1}{1+r_0}$ ，右边就剩下了所有 ${\psi }_1(\omega )$ 之和）

也就是 Implication 5 $\Rightarrow$ Implication 6

对于任意 $d\in \mathbf{D}$ ，我们有：
$${\Psi }_0(d)=\frac{1}{1+r_0}{\mathbf{E}}_{\mathbf{Q}}[d_1+{\Psi }_1(d)|{\mathcal{F}}_0]=\frac{1}{R_0^f}{\mathbf{E}}_{\mathbf{Q}}[d_1+{\Psi }_1(d)|{\mathcal{F}}_0]$$
（可以看到 $\mathbf{Q}(A)$ 的分母就是 $\frac{1}{1+r_0}$ ）

也就是说，0 时刻的定价等于其近期未来股息支付加上其市值之和的贴现价值。

风险中性定价规则可以扩展到任意时间段:
$${\Psi }_t(d)=\frac{1}{R_t^f}{\mathbf{E}}_{\mathbf{Q}}[d_{t+1}+{\Psi }_{t+1}(d)|{\mathcal{F}}_t]$$

Implication 7: Risk-free Return Rule

无风险收益规则：对于任意 $d\in \mathbf{D}$ ，记时刻 $t$ 的总收益率为：
$$R_{t+1}^d=\frac{d_{t+1}+{\Psi }_{t+1}(d)}{{\Psi }_t(d)}$$
在风险中心概率测度 $\mathbf{Q}$ 下，对于任意现金流串 $d\in \mathbf{D}$ ，其期望收益率都是一样的，为无风险利率，即：
$${\mathbf{E}}_{\mathbf{Q}}[R_{t+1}^d|{\mathcal{F}}_t]=1+r_t=R_t^f,\forall t$$

The Fundamental Theorem

$\mathbf{Q}$ 和 $\mathbf{P}$ 是不一样的，$\mathbf{P}$ 代表的是未来某些状态出现的概率，$\mathbf{Q}$ 则是正好满足概率的性质，所以定义了这样一个辅助量。并且在不完全的市场上，满足无套利性质的 $\mathbf{Q}$ 是不唯一的。

Theorem：在有限经济中，$M3$ ，$S1$ ，性质 5，性质 6 和性质 7 是相互等价的。并且和性质 1-4 的组合也是等价的。

• $M3⟺S1$ 前面已经证明过了；

• $S1⟺(1),(2),(3)\text{and}(4)$ 可以通过正比例函数的性质得到；

• $S_1\Rightarrow (5)\Rightarrow (6)\Rightarrow (7)$ 都是在描述性质 5、6、7 时就证明了；$(7)\Rightarrow M3$ 在下面的练习中证明：

Exercise 2：在风险中性概率测度下，对于某个现金流串 $d\in \mathbf{D}$ ，请证明其初始价格 ${\Psi }_0(d)$ 可以表示为以下形式：
$${\Psi }_0(d)={\mathbf{E}}_{\mathbf{Q}}\left[\sum _{t=1}^T\frac{d_t}{R_0^f\cdots R_{t-1}^f}+\frac{{\Psi }_T(d)}{R_0^f\cdots R_{T-1}^f}\right],\forall T\ge 1$$
证明：我只会倒推，就是把右边这个拆开，就可以得到初始时刻的价格。根据 Implication 6，我们有：
$${\Psi }_t(d)=\frac{1}{R_t^f}{\mathbf{E}}_{\mathbf{Q}}[d_{t+1}+{\Psi }_{t+1}(d)|{\mathcal{F}}_t]={\mathbf{E}}_{\mathbf{Q}}[\frac{d_{t+1}}{R_t^f}+\frac{{\Psi }_{t+1}(d)}{R_t^f}]$$
则原式右边可以变为：
$$\begin{array}{rl}& {\mathbf{E}}_{\mathbf{Q}}\left[\sum _{t=1}^T\frac{d_t}{R_0^f\cdots R_{t-1}^f}+\frac{{\Psi }_T(d)}{R_0^f\cdots R_{T-1}^f}\right]\\ =& {\mathbf{E}}_{\mathbf{Q}}\left[\sum _{t=1}^{T-1}\frac{d_t}{R_0^f\cdots R_{t-1}^f}\right]+{\mathbf{E}}_{\mathbf{Q}}\left[\frac{d_T}{R_0^f\cdots R_{T-1}^f}+\frac{{\Psi }_T(d)}{R_0^f\cdots R_{T-1}^f}\right]\\ =& {\mathbf{E}}_{\mathbf{Q}}\left[\sum _{t=1}^{T-1}\frac{d_t}{R_0^f\cdots R_{t-1}^f}\right]+\frac{1}{R_0^f\cdots R_{T-2}^f}{\mathbf{E}}_{\mathbf{Q}}\left[\frac{d_T}{R_{T-1}^f}+\frac{{\Psi }_T(d)}{R_{T-1}^f}\right]\\ =& {\mathbf{E}}_{\mathbf{Q}}\left[\sum _{t=1}^{T-1}\frac{d_t}{R_0^f\cdots R_{t-1}^f}\right]+\frac{{\Psi }_{T-1}(d)}{R_0^f\cdots R_{T-2}^f}\\ =& {\mathbf{E}}_{\mathbf{Q}}\left[\sum _{t=1}^{T-2}\frac{d_t}{R_0^f\cdots R_{t-1}^f}\right]+{\mathbf{E}}_{\mathbf{Q}}\left[\frac{d_{T-1}}{R_0^f\cdots R_{T-2}^f}+\frac{{\Psi }_{T-1}(d)}{R_0^f\cdots R_{T-2}^f}\right]\\ =& \cdots \\ =& {\mathbf{E}}_{\mathbf{Q}}\left[\frac{d_1}{R_0^f}+\frac{{\Psi }_1(d)}{R_0^f}\right]\\ =& {\Psi }_0(d)\end{array}$$

二叉树期权定价模型

例：假设当前股票价格为 $100，并且你认为三个月后，股票价格将等可能地上涨 20% 至 $120 或下跌 10% 至 $90。假设 3 个月的无风险利率为 2%（虽然不可能这么高，但是为了方便计算）。考虑该股票的一个欧式看涨期权，期限为三个月，敲定价为 $100。则该期权当前的合理定价为多少？

解：一个简单的想法，考虑到期时期望收益的贴现值：
$$\frac{0.5\times (120-100)+0.5\times 0}{1.02}=9.80$$
但是这样是不合理的，可以举出套利的反例。假定当前期权价格为 $C_0=\text{$}9.80$ ，考虑如下的投资组合：

• 向银行借 $ 9,700 ；
• 买 113 股股票；
• 卖出 130 份期权。

则 0 时刻的现金流为：

$$d_0=170\times 9.8+9700-113\times 110=\$66$$

三个月后平仓并偿还银行的贷款，现金流为：
$$d_1=\{\begin{array}{ll}-170\times 20-9700\times 1.02+113\times 120=\$266& \text{if goes up}\\ -170\times 0-9700\times 1.02+113\times 90=\$276& \text{if goes down}\end{array}$$
说明当价格为 $C_0=\text{$}9.80$ 时，存在套利机会。我们用两种方法得到正确的期权定价：

Approach One：Risk-Neutral Pricing ：在风险中性概率测度下，令 $q_h>0$ 且 $q_l=1-q_h>0$ ，分别对应价格上涨和下跌的“概率”。由概率测度的归一性和 Implication 7 可得：
$$\{\begin{array}{l}{q}_h+q_l=1\\ 1.20q_h+0.90q_l=1.02\end{array}\Rightarrow \{\begin{array}{l}{q}_h=0.4\\ q_l=0.6\end{array}$$
根据 Implication 6，当前期权价格为：
$$C_0=\frac{0.4\times (120-100)+0.6\times 0}{1.02}=\$7.84$$
Approach Two：Dulplicate Pricing ：（这有点像凑数字）考虑下列投资组合：

• 向银行借 $\frac{60}{102}\times 100 $ $ ；
• 持有 $\frac{2}{3}$ 单位股票；

该投资组合在三个月内的结果收益很容易计算，即上涨状态为20美元，下跌状态为0美元。该组合在到期日的收益与标的期权的收益相一致，即二者的未来现金流一致。根据 Implication 1 的一价原则，期权的初始价格必须由投资组合的初始成本给出，即：
$$C_0=\frac{2}{3}\times 100-\frac{60}{102}\times 100=\$7.84$$

单期期权定价模型 A Signle-period Model

令无风险利率为 $R^f=1+r$ ，假设 $h>R^f>l$ ，并且令 q h ≡ Q ( { h } ) q_h\equiv \bold{Q}(\{h\}) qh​≡Q({h}) 且 q l ≡ Q ( { l } ) = 1 − q h q_l\equiv \bold{Q}(\{l\})=1-q_h ql​≡Q({l})=1−qh​ 。由无套利的无风险收益规则，我们得到一般形式：
$$\{\begin{array}{l}{q}_h+q_l=1\\ q_{h}h+q_{l}l=R^f\end{array}\Rightarrow q_h=\frac{R^f-l}{h-l}\text{ and }{q}_l=\frac{h-R^f}{h-l}$$
未定权益为 $X_T$ ；根据风险中性定价规则，初始市场价为：
$${\Psi }_0(X_t)=\frac{1}{1+r}{\mathbf{E}}_{\mathbf{Q}}[X_T]=\frac{1}{1+r}(q_h{X}_h+q_l{X}_l)$$
特别地，对于敲定价为 $X$ 的欧式看涨期权，初始价格为：
$$C_0=\frac{1}{1+r}\left[q_h(h{S}_0-X{)}^{+}+q_l(l{S}_0-X{)}^{+}\right]$$

• 其中函数 ( x ) + = max ⁡ { x ,   0 } (x)^+=\max\{x,\,0\} (x)+=max{x,0}
• $S_0$ 是初始的股票价格

二叉树期权定价模型 CRR Binomial Model

前提假设：

• 无风险利率的固定期限结构：$R^f=1+r$ ；
• 二分的股票收益：股票收益 { R t } t ≥ 1 \{R_t\}_{t\geq 1} {Rt​}t≥1​ 是相互独立的。每一时刻 $R_t$ 都可能上涨到原来的 $h$ 或下跌到原来的 $l$ ，并且假设 $h>1+r>l$ ；
• 该股票在整个过程（到期日及到期日之前）中都没有分红

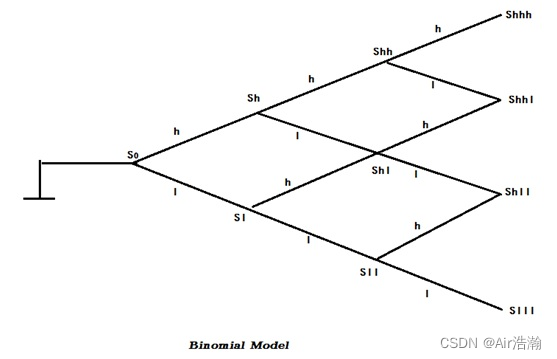
问题：确定未定收益 $X(S_T)$ 的当前价格。

事件空间 $\Omega$ 包括了在到期日之前所有二叉树上的路径：

• 例如对于 $\omega \in \Omega$ ，常见形式为 $(h,\cdots ,l,\cdots )$ ；
• $\Omega$ 中由 $2^T$ 条路径。对于任意时刻 $t$ 和任意状态 $\omega \in \Omega$ ，${\mathcal{F}}_t(\omega )$ 代表所有与 $\omega$ 共享 $t$ 时刻历史路径的所有未来路径。
  • $t=0$ ，${\mathcal{F}}_0(\omega )=\Omega$ ，$\forall \omega$ ；
  • $t\ge 0$ ，${\mathcal{F}}_0(\omega )$ ，$\forall \omega$ 共有 $2^{T-t}$ 条不同的路径；

按照无风险收益规则（Implication 7），存在风险中性概率测度 $\mathbf{Q}$ 使得：
$${\mathbf{E}}_{!}[R_{t+1}|{\mathcal{F}}_t(\omega )]=1+r$$
在测度 $\mathbf{Q}$ 下，下一时期股票收益为“高”值的概率为：
$$q_h(t,\omega )=\mathbf{Q}(R_{t+1}=h|{\mathcal{F}}_t(\omega ))=1-q_l(t,\omega )$$
无套利的条件要求对任意时刻：
$$q_h(t,\omega )=\frac{R^f-l}{h-l}=1-q_l(t,\omega )$$
在风险中性概率测度下，股票收益 { R t } t ≥ 1 \{R_t\}_{t\geq 1} {Rt​}t≥1​ 构成了独立同分布的二项过程，我们由此可以得到对 $X_T$ 的当前定价：

Proposition 1：到期日为 $T$ 的未来未定收益 $X(S_T)$ 的当前市场价为：
$${\Psi }_0(X)=\frac{1}{(1+r{)}^T}\sum _{m=0}^T\left(\genfrac{}{}{0ex}{}{T}{m}\right)q_h^m{q}_l^{T-m}X(h^m{l}^{T-m}{S}_0)$$

• $X(h^m{l}^{T-m}{S}_0)$ 应该是 $(h^m{l}^{T-m}{S}_0-S_0{)}^{+}$

证明：由于没有分红，到期日之前 $d_t=0$ ，因此根据风险中性定价规则（我觉得是根据 Exercise 2），有：
$${\Psi }_0(X)=\frac{1}{(1+r{)}^T}{\mathbf{E}}_{\mathbf{Q}}[X(S_T)]$$
显然，对于任意状态 $\omega \in \Omega$ ，其股票价格取决于路径上 h 和 l 的数量，所以就是上面那样的式子。

倒向过程 Backward Procedure

这个二叉树也可以倒过来看：

• 在时刻 $T$ ，${\Psi }_T(m)=X(h^m{l}^{T-m}{S}_0)$ ，$\forall 0\le m\le T$ ；
• 在时刻 $t\le T$ ，对于 $\forall 0\le m\le T$ ，价格为：

$${\Psi }_t(m)=\frac{1}{1+r}\times [q_h{\Psi }_{t+1}(m+1)+q_l{\Psi }_{t+1}(m)]$$

• 在初始时刻 $0$ ，价格为 ${\Psi }_0(0)$ ；

带有常数红利的期权定价 Option Pricing with Constant Dividend Yield

对于带有常数红利率 $\kappa$ 的股票，即 ${\delta }_t=\kappa S_{t-1},t\ge 1$ ，则风险中性概率变为：
$$q_h=\frac{R^f-\kappa -l}{h-l}=1-q_l$$
此时我们的假设要变为 $h+\kappa >R^f>l+\kappa$

例：对于某个欧式看涨期权给出以下具体数据：

• 常数红利率为 $\kappa =2\%$ ；
• 股票价格上涨或下跌的幅度为 $5\%$ ；
• 无风险利率为每期 $2\%$ ；
• 初始时刻的股票价格为 $$100$ ；
• 到期期限为 $T=5$ ，敲定价格为 $$100$ ；

股票价格过程为：

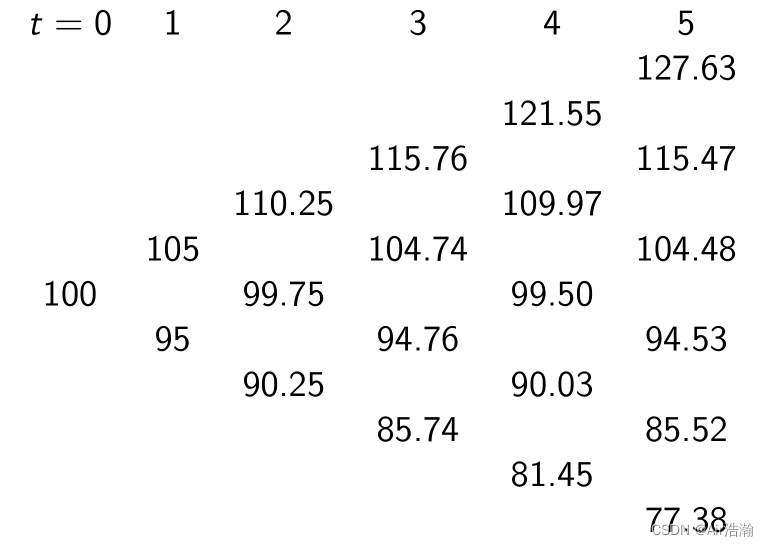
风险中性概率为：
$$q_h=\frac{R^f-l-k}{h-l}=0.5$$
倒向价格过程为：
$$C_{t,m}=\frac{C_{t+1,m}+C_{t+1,m+1}}{2\times 1.02}$$
期权价格过程为：

美式期权定价问题

美式期权在到期日及之前都可以行权，这里我们也是用二叉树期权定价模型，考虑离散的情况。

对于标的股票为 $S$ 的美式看涨期权，其敲定价为 $X$ ，在 $(t,\omega )$ 情况下的收益为：

• $t<T$ ：$X_t(\omega )=S_t(\omega )-X$ ；
• $t=T$ ：$X_T(\omega )=(S_T(\omega )-X{)}^{+}$ ；

（看跌期权就是相应地变为 $X-S_t(\omega )$ 和 $(S_T(\omega )-X{)}^{+}$）

直观理解一下，由于美式期权更为灵活，因此定价往往更高。离散时间的美式期权定价涉及到两个问题：

• 在时刻 $t<T$ 以及当时的信息 ${\mathcal{F}}_t(\omega )$ ，如何对该期权进行合理定价？
• 期权持有者选择在什么时间和什么状态行使他们的期权？

Theorem 5：美式期权的定价 { Ψ t ( X ) } t = 0 T \{\Psi_t(X)\}_{t=0}^{T} {Ψt​(X)}t=0T​ 和最佳行权时间 ${\tau }^{\ast }$ 满足：

1. 对于 $\forall (t,\omega )$ ，有：

$${\Psi }_t(X;\omega )=\max \left\{X_t(\omega ),\frac{1}{1+r}{\mathbf{E}}_{\mathbf{Q}}\left[{\Psi }_{t+1}(X)|{\mathcal{F}}_t(\omega )\right]\right\}$$

2. 对于 $\forall (t,\omega )$ ，${\tau }^{\ast }=t$ 当且仅当： ${\Psi }_s(X;\omega )>X_s(\omega )$ $\forall s<t$ 并且 ${\Psi }_t(X;\omega )=X_t(\omega )$ ，或者表述为：

τ ∗ ( ω ) = inf ⁡ { t ∈ { 0 ,   ⋯   ,   T } :   Ψ t ( X ;   ω ) = X t ( ω ) } ,   ∀ ω ∈ Ω \tau^*(\omega)=\inf\left\{ t\in\{0,\,\cdots,\,T\}:\,\Psi_t(X;\,\omega)=X_t(\omega) \right\},\,\forall\omega\in\Omega τ∗(ω)=inf{t∈{0,⋯,T}:Ψt​(X;ω)=Xt​(ω)},∀ω∈Ω

Proposition 6：考虑一个标的股票无分红的美式看涨期权，投资者在到期日之前都不会行权，即 ${\tau }^{\ast }\equiv T$ ，也就是说此时美式看涨期权和欧式看涨期权的定价相同。

证明：按照定义，美式看涨期权在 $(t,\omega )$ 情况下行权的的收益为 $S_t(\omega )-X$ ；并且按照 Th5 的性质 1，美式看涨期权的价值不低于同时刻的欧式看涨期权，即：
$$\begin{array}{rl}{\Psi }_t(X;\omega )\ge & \frac{1}{(1+r{)}^{T-t}}{\mathbf{E}}_{\mathbf{Q}}[(S_T(\omega )-X{)}^{+}|{\mathcal{F}}_t(\omega )]\\ \ge & \frac{1}{(1+r{)}^{T-t}}{\mathbf{E}}_{\mathbf{Q}}[S_T(\omega )-X|{\mathcal{F}}_t(\omega )]\\ =& S_t(\omega )-\frac{1}{(1+r{)}^{T-t}}X\\ \ge & S_t(\omega )-X\end{array}$$

• 第一个不等号是由 Theorem 5 给出，美式看涨期权的价值不低于同时刻的欧式看涨期权；

• 第二个不等号是因为 ( x ) + = max ⁡ { x ,   0 } (x)^+=\max\{x,\,0\} (x)+=max{x,0} ，所以 $(x{)}^{+}\ge x$ ；

• 第三个等号是因为期望的线性性，$\frac{1}{(1+r{)}^{T-t}}{\mathbf{E}}_{\mathbf{Q}}[S_t(\omega )]$ 根据 Implicatio 6 就是此时的价格；

• 第四个不等号是因为通常来说 $r>0$ ；

最后一个不等号意味着除非 $t=T$ ，否则 ${\Psi }_t(X;\omega )>S_t(\omega )-X$ ，那么投资者只会在 $t=T$ 时有可能行权（行权至少也要 $S_T(\omega )>X$ 吧hhh ）。

又根据 Implication 1 的一价定律，此时美式看涨期权和欧式看涨期权在初始时刻的定价相同。

当然，对于带分红的标的股票，Proposition 6 是不成立的。由于美式看涨期权的定价带有 $\max$ 运算，因此没法像欧式看涨期权一样写出正向解析式；对于某个具体的例子，我们可以通过倒向方程来推导。

例：对于某个美式看涨期权给出以下具体数据：

• 常数红利率为 $\kappa =2\%$ ；
• 股票价格上涨或下跌的幅度为 $5\%$ ；
• 无风险利率为每期 $2\%$ ；
• 初始时刻的股票价格为 $$100$ ；
• 到期期限为 $T=5$ ，敲定价格为 $$100$ ；

股票价格过程为（和前边欧式看涨期权一样）：

风险中性概率为：
$$q_h=\frac{R^f-l-k}{h-l}=0.5$$
倒向过程方程为：
$$A_{t,m}=\max \left\{S_{t,m}-K,\frac{A_{t+1,m}+A_{t+1,m+1}}{2\times 1.02}\right\}$$
期权价格过程为：

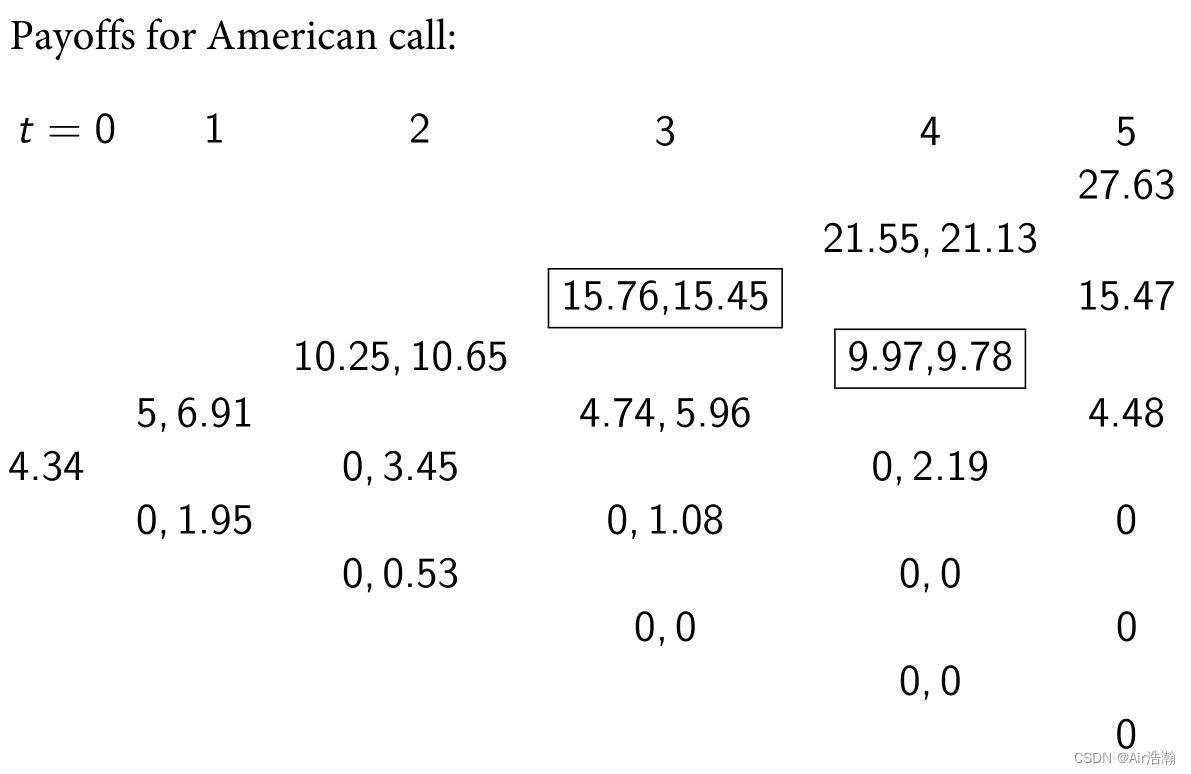
最佳行权时间为：

• 路径 { h ,   h ,   h } \{h,\,h,\,h\} {h,h,h} ，${\tau }^{\ast }=3$ ；
• 当不是三个连续的 $h$ ，但是有 3 个 $h$ （ { l ,   h ,   h ,   h } \{l,\,h,\,h,\,h\} {l,h,h,h} ， { h ,   l ,   h ,   h } \{h,\,l,\,h,\,h\} {h,l,h,h} 或 { h ,   h ,   l ,   h } \{h,\,h,\,l,\,h\} {h,h,l,h}），${\tau }^{\ast }=4$ ；
• 其他情况下，${\tau }^{\ast }=5$ ；

可以看到，和我们的直觉一致，在到期日之前，同时刻同状态下美式看涨期权的价格比欧式看涨期权要更高，但是在到期日是一样的。