分层强化学习代码汇总
0.综述
《The Promise of Hierarchical Reinforcement Learning》分层强化学习的前景
强化学习
强化学习问题的设置:
有两个主角:一个代理和一个环境。环境是代理所生活和交互的地方。在每一次交互中,代理都能看到世界状态的观察,然后决定要采取的行动。当代理对环境进行操作时,环境会发生变化,但它也可以自己变化。代理还会收到一个环境奖励信号,一个数字(或一个分布),它告诉代理行动的效果对于代理的目标来说是好是坏。
马尔可夫决策过程(MDP)用于描述强化学习中的环境,其中环境是完全可观察的。根据众所周知的马尔可夫性质“未来与过去无关,只与现在有关”,我们将一个有限MDP定义为一个元组<S,A,p,r>,其中S是一组有限的状态,A是一组有限的动作,p(s,a,s’)是一个分布,表示当从s采取动作a并进入下一个状态 s′时获得的奖励。一个静态的确定性策略 π:S → A,将状态映射为行动。
简而言之,在传统的强化学习问题中,智能体的目标是最大化其期望的折扣回报。

其中 rt 是智能体在时间 t 时收到的奖励, γ∈[0,1) 是折扣因子。在完全可观察的情况下,智能体观察到环境的真实状态 st∈S 并根据策略 π(a|s) 选择一个动作 at∈A。
一个解决强化学习问题的方法是定义一个被称为策略π的动作价值函数Qπ:

贝尔曼最优方程:

递归地代表了最佳的Q函数:

作为期望的即时奖励r(s,a)和转移函数P(s′|s,a)的函数,反过来产生了一个最优的贪婪策略
Q学习使用贝尔曼最优方程的样本近似来迭代地改进Q函数。在标准的随机近似假设下,Q学习已经被证明可以以概率1收敛于最优价值函数Q∗。它是一种用于求解马尔可夫决策过程的强化学习解决方案。在深度Q学习中,Q函数由一个神经网络表示,神经网络由参数θ表示。
强化学习的主要问题是:我们如何最大化未来的奖励?
回答这个问题实际上需要回答其他一些子问题,包括:我们应该学习什么(模型,状态效用,策略等)? 我们应该如何学习(时序差分学习,蒙特卡罗方法等)? 我们如何表示我们学到的东西(深度神经网络,大表格等)? 如何使用我们学到的东西:这往往是需要首先回答的问题…
与HRL相比,RL的弱点:
- 样本效率:数据生成通常是一个瓶颈,当前的强化学习方法是数据低效的。使用HRL,可以在同一领域的不同任务中使用子任务和抽象动作(迁移学习)
- 扩展性:将经典的强化学习应用于具有大规模动作和/或状态空间的问题是不可行的(维数灾难)。HRL旨在将大问题分解为小问题(高效学习)
- 泛化:训练过的智能体可以解决复杂的任务,但是如果我们希望它们将经验转移到新的(甚至相似的)环境中,大多数最先进的强化学习算法都会失败(由于过度专业化而导致的脆弱性)
- 抽象:状态和时间抽象可以简化问题,因为由此产生的子任务可以有效地通过强化学习方法来解决(更好的知识表示)
此外,所有的基本强化学习算法都是所谓的“平坦”方法。它们将状态空间视为一个巨大的、平坦的搜索空间,这意味着从起始状态到目标状态的路径非常长。此外,这些路径的长度决定了学习的成本,因为未来奖励的信息必须沿着这些路径向后传播。简而言之,奖励信号是弱的和延迟的。
也许我们可以退一步,看看我们到目前为止学到了什么:在20世纪70年代,规划领域的研究表明,分层方法,如分层任务网络,宏动作和状态抽象方法可以提供指数级的降低计算成本以找到正确的计划。还有大量关于子目标发现、内在动机和人工好奇心的文献。然而,我们仍然缺乏一种完全可接受的方法,将层次结构整合到迄今为止引入的有效的强化学习算法中。
分层强化学习(HRL):
正如我们刚刚看到的,强化学习问题存在严重的扩展性问题(HRL的背景)。
分层强化学习是一种计算方法,旨在通过学习在不同的时间抽象层次上进行操作来解决这些问题。
为了真正理解学习算法中分层结构的必要性,并为了在RL和HRL之间架起桥梁,我们需要记住我们要解决的问题是:MDP。
HRL方法学习一个由多个层组成的策略,每个层负责在不同的时间抽象层次上进行控制。事实上,HRL的关键创新是扩展了可用的动作集,使得智能体现在不仅可以选择执行基本动作,还可以执行宏动作,即较低层次动作的序列。因此,对于延伸时间的动作,我们必须考虑到决策时刻之间经过的时间。幸运的是,MDP规划和学习算法可以很容易地扩展以适应HRL。
为了做到这一点,我们迎来了半马尔可夫决策过程(SMDP)。

在这个设置中, p(s′|s,a) 变成 p(s′,τ|s,a) 。a是一个原始动作, σ是一个子程序或宏动作, π是动作策略, πσ 是子程序特定的动作策略,而 V 和 Va是状态值。
HRL的前景是拥有:
长期信用分配:更快的学习和更好的泛化
结构化探索:用子策略而不是原始动作进行探索
迁移学习:不同层次的层次结构可以包含不同的知识,并且可以实现更好的迁移
分层强化学习的基本框架:
封建学习
这种HRL方法的灵感来自于中世纪欧洲的封建制度,它展示了如何创建一个管理层次结构,其中领主(或管理者)学习分配任务(或子目标)给他们的农奴(或子管理者),而后者则学习满足他们。子管理者学习在命令的背景下最大化他们的强化。
在实践中,封建学习利用了两个概念:
信息隐藏:管理层次结构以不同的分辨率观察环境
奖励隐藏:管理者和“工人”之间通过目标进行沟通——达到目标就给予奖励
信息和奖励隐藏的一个值得注意的效果是,管理者只需要知道系统状态在他们自己选择的任务的粒度上。他们也不知道他们的工人为了满足他们的命令做了什么选择,因为系统设置不需要学习这些。
不幸的是,封建Q学习算法是针对一种特定类型的问题定制的,并且不收敛到任何明确定义的最优策略。但它为许多其他贡献铺平了道路。
选项框架
它提供了一种在 RL 中实现层次结构和宏动作(macro-actions)的方法。宏动作是指持续一段时间的动作序列,可以看作是高层次的抽象动作。选项框架中,一个选项(option)由三个部分组成:
- Io:启动集,表示可以开始执行该选项的状态集合。
- πo:选项的策略,表示在执行该选项时如何选择原始动作。
- βo:终止条件,表示在某个状态下该选项是否结束。
这个框架的思想可以通过上面的自解释示例来理解,其中选项可以总结为“走到走廊”,而动作可以是“向北、南、西或东走”。选项可以被视为更高层次的抽象动作(即每个状态都可以被用作子目标),并且因此可以被抽象为技能。
与封建学习不同,如果动作空间包含原始动作和选项,那么遵循选项框架的算法被证明能够收敛到最优策略。否则,它仍然会收敛,但是收敛到分层最优策略。
由此,选项框架由两个层组成:
- 底层是子策略:
- 进行环境观测
- 输出操作
- 运行直到终止
- 顶层是选项之上的策略:
- 进行环境观测
- 输出子策略
- 运行直到终止
选项框架的优点是可以利用时间抽象来简化问题,提高学习速度,并且有理论保证能收敛到最优或层次最优的策略。选项框架也可以用来定义多层次的结构,使得不同层次的选项可以相互调用。选项框架在 HRL 领域中有很多应用和扩展,例如 FeUdal Networks, Option-Critic Architecture, Data-Efficient Hierarchical Reinforcement Learning 等。
HAM
HAM的意思是分层抽象机,核心思想是通过先验知识设计状态机,降低MDP复杂度,再求解简化MDP的最优策略,也是典型的multi-level control
是将部分策略表示为一组具有不确定性的有限状态机,这些状态机的转换可能调用更低层次的机器(最优动作尚未确定或学习)。
HAM的目的是通过限制强化学习智能体在每个状态下可以采取的动作,来简化马尔可夫决策过程(MDP)。
HAM有四种机器状态:
- 选择状态:非确定性地选择下一个机器状态
- 停止状态:停止执行机器并将控制权返回给之前的调用状态
- 调用状态:调用另一个机器作为子状态并等待其返回
- 动作状态:在环境中执行一个原始动作并转移到下一个机器状态
当机器遇到调用状态时,它会以确定性的方式执行它应该执行的机器。当它遇到 Stop 状态时,它只是将命令发送回父计算机。与直接在 MDP 上学习的情况不同,MDP 在每个状态下学习操作,而在 HAM 框架中,学习仅在选择状态中进行。因此,发生学习的状态空间可能小于实际的状态空间。
学习机器的策略是决定调用哪台机器以及调用的概率。
HAM 框架为我们提供了通过限制可实现策略类别来简化 MDP 的能力。与选项框架类似,它也具有理论上的最优性保证。主要问题是 HAM 的设计和实施很复杂,并且可用的重要应用程序并不多。
HAM的优点是它可以实现时间和空间的抽象,提高学习效率和稳定性。HAM的缺点是它需要手工设计和实现机器结构,而且不能保证找到最优策略。
MAXQ
MAXQ是一种分层学习算法,其中通过将状态-动作对的Q值分解为两个分量Q(p,s,a)=V(a,s)+C(p,s,a)的总和来获得任务的层次结构,其中V(a,s)是当在状态s中执行动作a(经典Q)时获得的总期望奖励,C(p,s,a)是在执行动作a后,期望从父任务p获得的总奖励。事实上,动作a不仅可能包含一个原始动作,还可能包含一系列动作。
MAXQ相对于其他框架的优势在于它学习递归最优策略,这意味着给定其子任务的学习策略,父任务的策略是最优的。也就是说,任务的策略是上下文无关的:每个子任务都是最佳解决的,而无需参考执行它的上下文。虽然这并不意味着它会找到最佳策略,但它为状态抽象和更好的迁移学习打开了大门,并且可以为许多其他任务提供常见的宏操作。
简而言之,MAXQ框架提出了任务的真正分层分解(与选项相反),它促进了子策略的重用,并允许时间和空间抽象。尽管其中一个问题是MAXQ涉及非常复杂的结构,并且递归最优策略可能是高度次优的策略。
基本HRL框架特征的比较

近期工作
受到HRL的这些创始要素(封建,选项,HAM,MAXQ)的启发(或解释),近年来出版了一些有趣的文章,并取得了相当令人鼓舞的结果:
- FeUdal Network s(FUN) for Hierarchical Reinforcement Learning
- The Option-Critic Architecture
- HIRO (Data Efficient Hierarchical Reinforcement Learning)
- HAC (Learning Multi-Level Hierarchies with Hindsight)
- Locomotor Controllers
- On Reinforcement Learning for Full-length Game of Starcraft
- h-DQN
- Meta Learning Shared Hierarchies (MLSH)
- Modulated Policy Hierarchies (MPH)
- Stragetic Attentive Writer (STRAW) for Learning Macrow Actions
- H-DRLN
- Abstract Markov Decision Processes (AMDP)
- Iterative Hierarchical Optimization for Misspecified Problems (IMHOP)
- HSP
- Learning Representations in Model-Free HRL
HRL的未来
一方面,诸如更新分层代理级别所产生的非平稳性等挑战需要在实现方面付出更多努力,并引入额外的超参数。
另一方面,我们离实现合理的样品效率还很远。
这些缺陷是已知问题,与HRL的主要活跃研究方向完全一致,包括但不限于:
- 更好地管理更高级别的状态转换函数的非平稳性
- 自动学习层次结构
- 更高效的勘探在奖励稀疏的环境中通过高效分解来丰富信号
- 提高稳定性
1.FuN(2017)
《FeUdal Networks for Hierarchical Reinforcement Learning》
这篇论文介绍了一种新颖的分层强化学习(hierarchical reinforcement learning)架构,叫做封建网络(FeUdal Networks,FuN)。该架构受到封建强化学习(feudal reinforcement learning)的启发,通过在多个层次上解耦端到端的学习,实现了不同时间尺度的信用分配(credit assignment)。
研究目标:
提出一个能够有效地解决长期信用分配和记忆等难题,同时使得分层策略具有语义意义和结构化泛化的能力的架构。文章希望通过这种架构,能够在复杂的环境中实现高效的强化学习,并且能够生成可解释和可重用的子策略和子目标。
思想:
基于分层强化学习的FeUdal Networks(FuNs)架构,该架构由一个管理者(Manager)模块和一个工作者(Worker)模块组成。Manager在较低的时间分辨率上设定抽象的目标,通过一个隐含的状态空间传递给Worker。Worker根据Manager给出的目标在每个环境步骤上生成原始的动作。Manager和Worker之间没有梯度传递;Worker通过内在奖励来跟随目标,而Manager则通过环境奖励来学习选择潜在目标,以最大化外部奖励。
方法:
论文提出了一种新颖的、近似的转移策略梯度(transition policy gradient)方法来训练Manager,利用了目标所具有的语义含义。文章假设Worker的行为会最终与它被设定的目标方向一致,因此可以直接跳过Worker的行为,而根据预测的转移来进行策略梯度更新。
论文还提出了一种新颖的RNN设计,叫做dilated LSTM,它是Manager的循环网络,以较低的时间分辨率运行。dilated LSTM类似于dilated convolutional networks(Yu & Koltun, 2016),它将网络的完整状态划分为r个单独的子状态或“核”。在每个时间步t,网络只更新相应部分的状态,并将前c个输出进行汇总。这使得dilated LSTM内部的r个核能够保持长期记忆,同时整个dilated LSTM仍然能够处理和学习每个输入经验,并且能够在每个步骤更新其输出。延长了循环状态记忆的寿命,并允许梯度通过大跨度的时间步流动,实现了对数百步的有效反向传播。
研究方案步骤:
- 设计分层强化学习的模型架构,包括Manager模块和Worker模块,以及它们之间的目标传递和内在奖励机制。
- 提出一种新颖的、近似的转移策略梯度更新方法,用于训练Manager模块,利用它产生的目标的语义含义。
- 使用方向性而非绝对性的目标,使得Worker模块能够可靠地引起潜在状态中的方向变化,并且给目标提供一定程度的不变性和结构化泛化能力。
- 提出一种新颖的RNN设计——dilated LSTM,作为Manager模块的循环网络,以较低的时间分辨率运行,并且能够保持长期记忆和处理每个输入经验。
- 在ATARI游戏和3D DeepMind Lab环境中的一系列任务上进行实验,展示FuNs在长期信用分配和记忆方面的优异性能,并与基线方法进行对比。
- 进行消融实验,验证FuNs架构中的各个组成部分和设计选择的有效性和必要性。
创新:本文创新在goal实现了自动选取并赋予了很合理的语义解释。FuN笔记
代码:
FuNs的pytorch实现
结果:显示的结果是单次运行 Pong 13 万帧和 BreakoutNoFrameskip-v4 用于 100 亿帧。

2.SNN4HRL(2017)
《Stochastic Neural Networks for Hierarchical Reinforcement Learning》
它介绍了一种用于分层强化学习和随机神经网络的框架,该框架可以在预训练环境中学习一系列有用的技能,然后利用这些技能在下游任务中提高探索和解决稀疏奖励问题的能力。
文章分为以下几个部分:
- 介绍了分层强化学习和技能发现的相关工作和动机。
- 阐述了问题的形式化和结构假设。
- 描述了预训练环境的构建,使用代理奖励和信息论正则化来引导技能学习。
- 描述了随机神经网络的设计和优化,以实现多模态策略。
- 描述了高层策略的架构和训练过程,以利用预训练的技能解决下游任务。
- 报告了在一系列具有挑战性的稀疏奖励任务上的实验结果和分析。
研究目的:
是如何解决长期目标与稀疏奖励问题,以及如何学习一组技能来更高效地解决多种任务。提出了一种分层强化学习框架来解决这些问题。
研究方案:
是使用分层强化学习框架来解决稀疏奖励或具有较长时间跨度的问题。该方法涉及在预先训练的环境中学习一组技能,其中单个代理奖励信号引导学习过程,并且对下游任务的最小领域知识。学习到的技能然后可以用于通过节省样本的方式培训高层策略来解决一组任务。为了有效地预先训练大量技能,作者使用随机神经网络(SNN)与信息理论正则化器组合,以促进行为的多样性。
方法步骤:
首先需要进行预训练目的是为了学习有用的技能,预训练过程中为了鼓励智能体自己探索所以给予很少的专家领域知识。为了让智能体学到的技能更加多样,文章中引入了SNN(随机神经网络),SNN可以很容易表示多模态策略,同时实现权重共享,在SNN中采用双线性融合的方式将隐变量(子任务)和观测值串联起来输入到网络当中,产生更加多样的技能。

接下来,为了提高SNN学习技能的范围,在原有的奖励中加入了基于互信息的正则项:

最终学习一个上层控制器manager。预训练SNN会学习很多技能,高层根据观测的状态信息在这些技能里调用一个技能让下层执行。对于上层和下层策略的训练,文中使用信赖域策略优化(TRPO)作为策略优化算法。snn4hrl可以学习到多样的技能,能够在一系列稀疏奖励任务中表现出色,实现迁移效果。该方法的局限性在于智能体在技能之间的切换问题。
研究成果:
实验表明,该框架可以以节省样本的方式学习可解释的技能,并且可以显着提高对具有长时间跨度和稀疏奖励的各种挑战任务的学习性能。该方法集成了内在动机和分层方法的优点,使代理可以探索自己的能力,而不需要任何特定于每个下游任务的目标信息或传感器读数。总体而言,分层策略学习框架在学习各种技能方面非常有效,并且可以减少样本复杂性,并在具有挑战性的真实任务上获得强大的性能。
文章的主要贡献是提出了一种通用且有效的框架,可以在最小监督下学习多样且可解释的技能,并在稀疏奖励任务上表现出优异的性能。
代码:用于分层强化学习的随机神经网络
结果:演示视频
3.VIME(2017)
《VIME:Variational Information Maximizing Exploration》
VIME是一种基于最大化奖励函数信息收益的探索策略,通过贝叶斯神经网络和变分推理等技术来处理高维深度强化学习场景下的有效和可扩展的探索方法。它能够优化智能体的好奇心并在多个不同的强化学习算法中应用。在多个连续控制任务中对VIME进行实验评估时,与简单的探索策略相比,VIME表现出更好的学习表现。
研究背景:
强化学习中的主要问题是探索和开发之间的权衡。传统解决这个问题的方法是使用贝叶斯强化学习和PAC-MDP方法来自动平衡探索和开发。这些方法适用于离散状态和行动空间的小任务。但是,在高维深度强化学习场景中,这些方法无法有效地进行状态-动作离散化。因此,许多强化学习算法使用启发式探索策略,例如epsilon-greedy,Boltzmann exploration和Gaussian策略。这些方法通常依赖于随机漫步行为,效率往往很低。
因此本文针对高维深度强化学习场景中探索方法的可扩展性和有效性进行探讨,提出了一种名为变分信息最大化探索(VIME)的新型探索策略,利用变分推断来最大化智能体对环境动态的信念的信息增益。其中,Bayesian neural network(BNN)模型被用于测量压缩改善,并等同于智能体的好奇心。 VIME 修改了 MDP 奖励函数,并可以与多种不同的 RL 算法一起使用。 该方法在多个连续控制任务和多个基本 RL 算法上进行评估,并显示出比朴素探索策略更好的表现。 本文还介绍了相关工作,并概述了结合信息增益和压缩改善的未来工作的潜力。
VIME基本原理
VIME 的基本原理比较简单。对于一个transition(s_t,a_t,s_{t+1}) ,如果s_{t+1} 的状态转移能够很大的减少环境模型θ的不确定性,则应该给予很大的奖励。用信息论的方法表示该理论是,如果 s_{t+1},θ 在 s_t,a_t 条件下的互信息越大,则内在激励越大。二者的条件互信息表示为:

研究方案:
本文的研究目标是探索一种新的强化学习探索策略,称为变分信息最大化探索(VIME),旨在解决高维度深度强化学习场景中探索方法的可扩展性和有效性问题。通过使用变分推断来最大化关于代理程序对环境动态的信念的信息增益,以贝叶斯神经网络(BNN)测量压缩改进,将其与代理程序的好奇心对等,来达到目的。 VIME可以修改MDP的奖励函数,并可应用于多种不同的基础强化学习算法。在多种连续控制任务和多个基础RL算法上进行评估,VIME相比朴素的探索策略实现了显着更好的性能。最后总结了相关工作,并概述了未来结合信息增益和压缩比例改善的研究前景。
本文的研究方案是使用变分信息最大化探索 (VIME) 策略探索强化学习,通过贝叶斯神经网络 (BNN) 使用变分推断来最大化有关代理相信环境动态的信息增益,从而解决高维深度 RL 场景中探索方法的可扩展性和有效性问题。VIME 修改了 MDP 奖励函数,并可与多种基础 RL 算法配合使用。具体实现步骤包括建立符号,解释好奇心驱动探索的理论基础,对连续控制进行适应,并使用变分推断实现这一概念,建立良好的压缩改进模型,从而实现对环境动态信念的增加。实验表明,VIME 策略显着优于 Naïve 探索策略。将来可以探索信息增益和压缩改进结合的潜力。
具体过程
探索的原则
目的是在不考虑外部奖励的情况下,决定如何探索,即如何选择下一步的行动 at 。这里维护一个对于环境动力学的建模 p(s_{t+1}|st,at,θ),θ∈Θ, 而该模型的参数Θ看做是一个随机变量,θ是该随机变量的值。选择行动的目标就是最大化该行动之后对于模型来说获得的信息增益,也就是希望每一步行动都能够尽可能利用这次交互机会来更多地获取环境的信息。具体地,就是每一步要最大化
其中 ξt={s1,a1,⋯,st}表示之前的轨迹。
转为为内在奖励形式
考虑到[1][2]


(1)式就等于

要通过最大化这个互信息来选择行动实在有点困难,一般行动是由策略决定的,策略是由RL的算法结合奖励学出来的,因此,我们就想,干脆把它做成内在奖励。于是有:
内在奖励计算

使用Variational Bayes方法
对于这样的困难有一套比较成熟的解决思路了[3][4],我们使用一个参数化的规则的分布 q(θ;ϕ)来近似复杂的分布 p(θ|D)。在这里我们选择fully factorized Gaussian distribution

其中, ϕ={μ,σ}。在这样的情况下,内在奖励就可以写成可以计算的形式了

更新参数Φ

在优化过程中,我们需要对参数 φ 进行更新,以最大化 L[q(θ; φ), D]。根据变分推断的推导过程,我们可以使用梯度上升算法来更新参数φ。具体步骤如下:计算目标函数的梯度。根据目标函数的定义,梯度可以通过求偏导得到:∇φ L[q(θ; φ), D] = Eθ∼q(·;φ)[∇φ log p(D|θ)] − ∇φ DKL[q(θ; φ)kp(θ)]更新参数φ。使用梯度上升算法,更新参数φ:φ ← φ + α ∇φ L[q(θ; φ), D]其中,α 是学习率,控制每次更新参数的步长。重复步骤1和步骤2,直到目标函数收敛或达到一定的迭代次数。注意,更新参数φ的过程中,需要计算和优化的是目标函数的极大值,而不是最小值。因此,我们使用梯度上升算法,而不是梯度下降算法。
计算内在奖励
内在奖励形式:



下面最关键的来了,注意到奖励可以写成

注意到(12)式里当 ϕ′ 在 ϕ_{t-1} 附近的时候,后一项主要是线性的,只有前一项有二次型的形态,因此Hessian矩阵可以只算前一项的。考虑到高斯分布参数化之后,KL散度计算十分方便,因此(13)式的 H(l)很容易计算得到。同时注意到,Hessian只有对角项,因此其逆H^{-1}(l)也很容易求。 ∇ϕl再次利用reparametrization trick一样可以求到。
算法:

代码:VIME的pytorch实现
实现:


4.MLSH(2018)
《Meta Learning Shared Hierarchies》
核心思想:
本文提出了一种新的meta-learning的方法,meta-learning shared hierarchies (MLSH),结合了hierarchical RL的思想,旨在从一个task distribution中学习到shared 多个subpolicy,并在面对一个unseen task的时候,能够基于这些subpolicy,fine-tune一个master policy在subpolicy上进行manipulate。类似distribution中的多个task share 相同的subpolicy,这一idea直观上非常reasonable,且master policy(HRL的high level)在较大的time scale上决策,能够进行快速的learning文章的实验对实际learning得到的subpolicy的质量以及其transfer performance进行了评估,均得到的符合假设预期的结果。
研究方案
结构
首先,定义了一个分层策略的结构,包括一个主策略和一组共享原语。主策略是一个任务特定的策略,负责在每个N个时间步(例如N=200)选择一个共享原语来执行。共享原语是一组任务无关的策略,负责在每个时间步选择一个动作来执行。

优化问题
其次,提出了一个优化问题,用于寻找一组能够在未见过的任务上快速达到高奖励的共享原语。优化问题的目标函数是衡量分层策略的强度的一个具体指标,即在新任务上训练主策略的样本效率。
优化算法
- 然后,提出了一个优化算法,用于近似地求解优化问题。优化算法的核心思想是通过使用任何现成的强化学习方法,不断地采样新任务并重置任务特定的主策略,来端到端地更新共享原语。

整个训练分为两个阶段: warmup 阶段和joint update阶段
在warmup更新阶段,fix现有的子策略参数φ ,仅对master policy超参数θ进行更新。用任何RL 算法都可以。如下图,更新仅与observation,master action 和master reward有关

在joint update更新阶段,同时对φ和θ进行更新。值得注意的是,对φ更新的时候仅对在这个短时期激活的子策略超参数进行更新。并将master action当作是observation的一部分(这里我不太理解,我觉得完全不忽略也可以)。

实验框架
最后,提出了一个实验框架,用于评估优化算法在不同任务分布上的性能。实验框架包括了一些机器人控制的任务,如四足机器人在迷宫中移动、三维人形机器人行走和爬行等。
研究成果
- 提出了一种用于分层策略的端到端金属学习的方法。
- 提出了一个将共享信息表示为一组子政策的模型。
- 提供了一个框架,用于在环境的分布上训练这些模型。
- 尽管没有优化真正的目标,但在学习中取得了明显的速度。
- 此外,发现不同的子政策,而不需要手工工程。
实验结果
2D moving bandits
在相对简单的2D moving bandits问题中,MLSH成功学习到了往左/往右的subpolicy,而shared policy进行学习,只能converge到某一个target上

4 Room
HRL经典的4 room问题中,MLSH取得了比PPO更快的learning,而OC效果并不好

physical continuous control task
在continuous control task中, MLSH也成功学到了meaningful的subpolicy




other unsolvable task
Figure 7 中的task是PPO不能解决的task,reward sparse,unpassable wall and chasing enemy,运用上述实验中Ant的subpolicy,MLSH进行master policy的fine-tune,成功取得了一定的performance。

代码:元学习共享层次结构
总结
- MLSH的idea很自然,简单有效,temporal abstraction的做法和common 的 HRL方法基本一致
- 需要注意的一点是,通常single task中,为了training的稳定性,会keep master policy random,warmup subpolicy,这是希望master policy能在subpolicy有一定level之后,再进行有效learning;
而MLSH中,则是warmup master policy,这一点是因为问题的侧重不同,MLSH/meta-learning关注的multi-task setting,正如formulation中所提的,MLSH的目的是学习到对一个task distribution都行之有效的subpolicy。
这些subpolicy是multi-task shared,而master policy则是对specific task进行quick adaptation - 感觉MLSH需要相当程度的engineering才能比较好的training出结果,这一点同样对HRL和meta-learning的training很重要
5.HIRO(2018)
《Data-Efficient Hierarchical Reinforcement Learning》
HIRO是一个HRL的算法,可以解决稀疏奖励和延迟信用分配的问题。
本文提出了一种适用于off-policy算法的分层模型,该模型与FeUdal十分类似,均基于subgoals,且high-level policy产生的goals均包含与状态转移有关的语义特征。所不同的只是FeUdal侧重于网络模型和相应训练方法的设计,而本文则是简明介绍了分层架构,同时提出了在该架构中使用off-policy算法所存在的问题与相应的解决方案。但相较而言模型更加简单.
研究背景:
前期分层强化学习算法中存在的两个问题:
- 许多算法需要针对每个任务进行一些人为的设计,例如H-DQN算法中,需要对事先设定goals;
- 许多算法都需要用on-policy的RL算法进行训练,这是因为每个high-level策略对应的low-level策略通常处于不断变化的过程之中,因此过去某一时刻的high-level策略所能产生的low-level动作与未来不一定相同,这导致了high-level策略的非平稳问题,使得过去的样本无法有效地应用在训练之中。
过程:
算法框架:

分层为两层,分别是higher-level policy和lower-level policy。上层策略每隔c步调用一次,产生一个目标,下层策略在这c不里面尽量去完成这个目标,上层策略和下层策略分别用现有的off-policy RL算法去训练,这里使用的是TD3。
定义上层策略产生的目标
上层策略产生的目标gt定义为原状态空间里面的变化,即希望下层空间在c步里面由st变成st+gt。
下层策略的状态除了原MDP的状态之外,还输入上层策略给定的目标gt。
由于下层策略的时间粒度更细,因此每一步都需要对上层空间给定的目标做一个转化,即
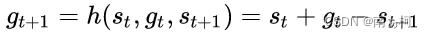
定义下层策略的奖励
需要根据上层空间给定的这个含义明确的目标定义下层策略的奖励,定义方法很直观,就是状态空间里面的L2距离。

off-policy修正

结果:
代码:
在 PyTorch 中实现数据高效的分层强化学习(HIRO)





6.SeCTAr(2018)
《Self-Consistent Trajectory Autoencodr: Hierarchical Reinforcement Learning with Trajectory Embeddings》
研究背景
- HRL是一种解决时间延长和稀疏奖励问题的方法,它可以通过学习低层次的原始动作来构建高层次的策略。现有的层次强化学习方法大多是自顶向下的,需要预先定义目标、抽象动作、子任务、技能或选项等,这些往往不容易确定,并且可能限制了探索和泛化能力。
- 本文提出了一种从表示学习的角度来看待层次强化学习的方法,将学习低层次的原始动作转化为学习轨迹级别的生成模型,即SeCTAR。
- SeCTAR可以学习连续的轨迹隐变量表示,有效地解决了时间延长和多阶段问题。它的核心思想是学习一个隐变量条件的策略和一个隐变量条件的模型,使它们相互一致。给定相同的隐变量,策略生成的轨迹应该与模型预测的轨迹匹配。这个模型提供了一个内置的预测机制,通过预测闭环策略行为的结果。
- 本文还提出了一种利用这个模型进行层次强化学习的新算法,结合了在学习到的隐变量空间中进行基于模型的规划和无监督探索目标。实验结果表明,该模型在几个模拟任务中表现出了优于标准强化学习方法和先前方法的推理能力。
研究方案
这篇论文的实际的主要工作分为两个部分:
- 构建了一个skill的连续潜在空间
- 提出了一个能够同时学习产生skill和预测它们结果的概率隐变量模型。
SeCTAR 模型

上面是SeCTAR model的计算图,可以看出SeCTAR模型包含两个decoders:
state decoder用来将latent variables解码成状态序列,
policy decoder是一个latent conditioned policy能够生成encoded trajectory。

State Decoder可以预测实际的状态序列,但是没有办法得到确切的行为序列,因此需要一个Policy Decoder去实际表示action policy,然而又由于Policy Decoder没办法直接生成完整的轨迹(如图所示,就是一个skill所在的时间范围),所以需要State Decoder去提供下完整的状态序列。
这个two-headed model能够让state decoder作为一个对于行为的预测模型,同时policy decoder也可以在环境中实际执行。
State Decoder训练:

State Decoder部分的训练是最大化上述这个期望,这个期望中前一部分是为了拟合观测到的数据,而后一部分是拟合Policy Decoder——Policy更新了对应的State序列也要变。
policy decoder训练:

Policy Decoder部分类似,前一部分是为了拟合State Decoder生成的序列(给出对应的Action),后一部分是个熵正则化项。
整体的训练过程
可以如下表示:State Decoder更新拟合实际产生的State序列(并一定程度上拟合Policy),然后得到新的State Decoder,接着Policy Decoder再去根据新的State Decoder去更新自己的策略来更新Policy。那么在最终得到的隐变量z其实就表达了我们要学习的skill了。

算法


代码:自洽轨迹自动编码器
实验结果


我们的方法与之前的2D导航、轮式运动、物体操作和游泳者航点方法的最佳设置进行了更新的比较。游泳者航点的任务是新的–游泳者每正确游过3个航点,就会得到1的奖励。
在这些更新的比较中,我们使用了PPO-选择批评器,它比DQN-选择批评器的表现好得多,而且还对基线进行了更广泛的超参数扫描。 虚线表示截断的执行。我们发现,在所有的任务中,我们的方法能够比基于模型、无模型和分层基线更快地获得更高的奖励。我们没有评估FeUdal和A3C在轮式运动和游泳任务中的表现,因为我们对这些方法的实现只考虑了离散的动作。
结论
- 提出了一种分层强化学习的方法,它结合了轨迹的表征学习与基于模型的规划在一个连续的潜在空间的行为的连续潜在空间中,将轨迹的表示学习与基于模型的规划结合起来。
- 描述了如何训练这样一个模型并将其用于训练这种模型,并将其用于长水平线规划以及探索。
- 实验评估表明,我们的方法在需要对长时空进行推理的任务中优于先前的几种方法和平面强化学习方法在需要对长视野进行推理的任务中,处理稀疏的奖励,以及执行多步骤的复合技能。
7.LSP(2018)
《Latent Space Policies for Hierarchical Reinforcement Learning》
研究背景:
- 模型无关的深度强化学习在许多具有挑战性的领域展现了潜力,从游戏到操纵和运动任务等。
- 将深度表示引入强化学习的部分前景是能够产生层次结构,这可以使得在不同层次的抽象上进行推理和决策。
- 一个层次强化学习算法原则上可以有效地发现复杂问题的解决方案,并在相关任务之间重用表示。
- 这些方法的一个核心挑战是层次结构构建过程的自动化:手工指定的层次结构需要相当的专业知识和洞察力来设计,并且限制了方法的通用性,而自动化的方法必须应对严峻的挑战,例如所有原始技能都崩溃为一个有用的技能或者需要手工设计原始技能发现目标或中间目标等。
研究目标:
- 设计一种层次强化学习算法,可以以自底向上的逐层方式构建层次表示。
- 提出一种基于隐变量的策略来构建层次结构,每一层的策略都有内部的隐变量,这些隐变量决定了策略如何将状态映射到动作,而下一层的隐变量则作为上一层的动作空间。
- 通过最大熵强化学习目标使每一层获得一系列多样的策略,并通过约束隐变量到动作的映射是可逆的保证高层次保持完全的表达能力。
- 在标准的基准任务和稀疏奖励任务上进行实验评估,证明该方法可以通过增加额外的层次来提高单层策略的性能,并且可以通过在优化简单低层次目标的高熵技能之上学习高层次策略来解决更复杂的问题。
研究方案:
- 首先,作者提出了一个分层的神经网络策略模型,其中每一层都是一个高斯策略,其均值和方差都是由神经网络参数化的。每一层都有一个隐变量 z ,其服从一个先验分布 p(z) ,并且在训练时从该分布中采样。每一层的策略输出 a 是由 z 和当前状态 s 共同决定的,即 a = f(z,s) ,其中 f 是一个可逆的函数。
- 然后,作者设计了一个分层的最大熵强化学习目标函数,其基本思想是让每一层都最大化其期望奖励和熵。具体来说,对于第 i 层策略 π_i ,其目标函数为:
- J(πi)=Eτi∼πi[r(τi)+αH(πi(ai∣si,zi))]其中 τi 是第 i 层策略产生的轨迹, r(τi) 是轨迹的奖励函数, α 是熵系数, H(πi(ai∣si,zi)) 是第 i 层策略在给定状态 s_i 和隐变量 z_i 时的条件熵。
- 接着,作者使用了软 Q 学习算法来优化每一层策略的目标函数。具体来说,对于第 i 层策略 π_i ,作者定义了一个软 Q 函数 Q_i ,其满足以下贝尔曼方程:Qi(si,ai,zi+1)=r(si,ai)+γEsi+1∼p[Vi+1(si+1,zi+1)]其中 Vi+1(si+1,zi+1) 是第 i+1 层策略的软价值函数,其定义为:Vi+1(si+1,zi+1)=Eai+1∼πi+1[Qi+1(si+1,ai+1,zi+2)−αlogπi+1(ai+1∣si+1,zi+1)]
作者使用了一个神经网络 Q 网络来近似 Q 函数,并使用了一个目标网络来稳定训练过程。作者使用了最小二乘法来更新 Q 网络参数 θ ,使得 Q 网络输出与目标网络输出之间的均方误差最小化:θmin21∥Qθ(si,ai,zi+1)−y
理论推导:概率图模型&变分推导
最大熵强化学习的介绍见SAC,优化目标为

在理论推导中,把强化学习的最优控制问题:如何决定动作以获得最优未来?转化为概率图模型的推理问题:给定未来最优,如何选择采取哪个动作?

概率图模型
推导基于上图(a)所示的概率图模型,包含概率转移p(s_{t+1}|s_t,a_t)和动作先验分布p(a_t)。我们的目的是在给定reward函数下,推导最优轨迹分布,为每一state-action 对引入一个二值随机变量O_t,用来表示当前时间步是否为“最优”。我们的目标是推导出后验动作分布π*(a_t|s_t)=p(a_t|s_t,O_{t:T}),即最优动作能使从当前到未来所有状态都是最优的。
且p(O_t|s_t,a_t)=E(r(s_t,a_t)),则最优轨迹分布可以写为:

我们可以利用这个分布来进行查询,如p(a_t|s_t,O_{t:T}),下面我们将使用变分推断将查询p(a_t|s_t,O_{t:T})转化为最大熵强化学习问题。
变分推断
上式推导出的最优动作分布不能直接作为策略。首先,它会导出一个过于乐观的策略甚至假定转移概率也可以被修改以偏好最优行为;其次,在连续动作情况下,最优策略往往难以处理,必须进行近似。我们使用结构化的变分推断来修正这两个错误。我们限制转移概率和真实环境一致,并且将策略限制为某些参数化的分布,则变分分布q(τ)定义为:

其中π(a_t|s_t)为待学习的参数化策略,我们通过最大化证据下界来近似它:

上式的推导为:

则:
由于p 和q的初始状态和转移概率都相同,则上式可简化为:

如果我们选择先验动作分布为一个均匀分布,则我们就导出了上面所示的最大熵目标。
模型:Latent Space Policy
潜变量策略
我们定义基础策略,包括:一个条件动作分布π(a_t|s_t,h_t),其中h_t是一个潜随机变量;一个先验分布p(h_t)。该策略的动作生成方式为:首先从先验中采样h_t,再根据条件分布生成a_t。
h_t的添加导出了一个新的图模型,基础策略被结合进MDP的状态转移里去:

新模型与旧模型有相似的语义,且有一组新的,更高层的动作h_t。
我们可以多次重复该过程,建立起一个任意深的分层表示。
训练
基础策略采用从潜变量到动作的双射a_t=f(h_t;s_t),使用real NVP,则a_t的概率密度表示为:

模型结构
下图右侧是整个的模型结构。左侧展示了每一层的具体结构,s_t下面是两个全连接层用于生成 state embedding,h_t^{(i+1)}下面是两个耦合层coupling layer in real NVP

算法
轮流训练每一层,冻结其权重,然后把下一层的潜变量作为动作空间训练新的层,每一层都使用相同的最大熵目标,每一层都为上一层简化任务。在实现中,每一层都使用SAC作为基本算法优化最大熵目标。

代码:Soft Actor-Critic
实验结果:
最优性

多层影响

其他比较

8.HAC(2019)
《Learning Multi-Level Hierarchies with Hindsight》
与HIRO一样,本文解决的同样是分层强化学习中不同层级策略学习所存在的非平稳问题,但是用了完全不同思想的方法。另外,HAC可以看做是HER在分层结构中的扩展。分层强化学习通过将任务分解成多个子任务,样本利用率更高。然而,在分层结构中,上层的转移函数取决于下层的策略,当所有层级的策略同时进行训练时,下层策略不断更新,这就导致了上层的转移函数会随之不断变化,在这样的非平稳环境中,智能体很难学习到最优策略,这就是分层强化学习所面临的非平稳(non-stationary)问题。当前大多数分层强化学习算法一次只能训练一个层级,为了并行地训练多个层级,本论文的主要思路是:当下层的任务收敛到最优或次优时,上层策略就可以进行稳定训练了。基于这一思想,本文提出了Hierarchical Actor-Critic (HAC),主要创新点是设计了三种transition样本用于训练。
算法框架:
算法框架本文利用了一种嵌套的方式构建了多层智能体。如下图所示,开始交互时,与环境交互的优先权在Worker3,这时状态输入Worker3,生成子目标Subgoal2。同时,环境优先权到达Worker2上,生成子目标Subgoal1。同样,这时环境优先权到达最底层的Worker1上,生成动作Action与环境交互。当最底层的Worker1完成交互后,环境的优先权逐层上传。本算法通过递归地调用自身完成。
创新之处:利用Hindsight Experience Replay(HER)克服多层智能体同时训练难点,这是本文的最大亮点。训练多层的难度在于non-stationary state transition functions。
在分层强化学习中,造成转移函数非平稳性的原因有两个:
1)低层策略的不断更新;
2)低层策略为了探索而采用行为策略(behavior policy)
例如确定性策略中,在生成的动作上加入额外的噪声。为了克服非平稳性,HAC在训练每一层策略时,假设下层策略是最优的,即 Π*_i−1。Π*_i−1 独立于变化或者探索中的下层策略,因此是平稳的。

简单来说,Hindsight action transitions包含两个重要组成部分(transition表示一个状态转移元组):
- transition中的action是事后已经达到的状态,而非之前所提出的subgoal状态。
- transition中的reward只与目标以及事后达到的状态有关,即如果goal没有达到,奖励就为-1,达到了就为0。
以上图中所展示的两层任务为例,其中上层任务在s1 时的 Hindsight action transitions为:[initial state=s0,action=s1,reward=0,next state=s1,goal=yellow flag,discount rate=gamma](原本的动作是 g0,由于智能体事后到达了状态s1,所以将动作改为了 s1)这一转移达到的效果与高层策略选择 s1 作为目标且下层策略是最优策略时达到的效果一致。
算法流程:
简而言之就是在原理DDPG算法的基础上,加入分层结构,为了提高不同层之间非平稳性不能并行训练的问题,在分层结构上加入hindsight的思路修改扩充经验回放池中的数据进行训练。因此算法的流程实际上就是产生不同样本的流程。

仿真结果:


- 分层比不分层好,3层比2层好;
- HAC比HIRO好










![【P1003 [NOIP2011 提高组] 铺地毯】](https://img-blog.csdnimg.cn/img_convert/b747d88a6ba85b589e77c2e1862445d3.png)