---

一、Tire树的概念

Trie树又称字典树、单词查找树。是一种能够高效存储和查找字符串集合的数据结构。

示例：

利用Tire树的数据结构储存字符串
储存完之后再进行末尾标记

省略根节点：

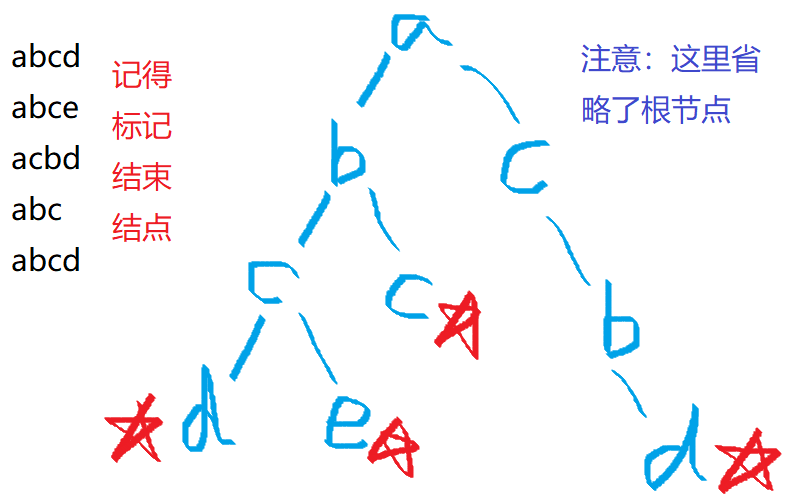
无省略根节点：

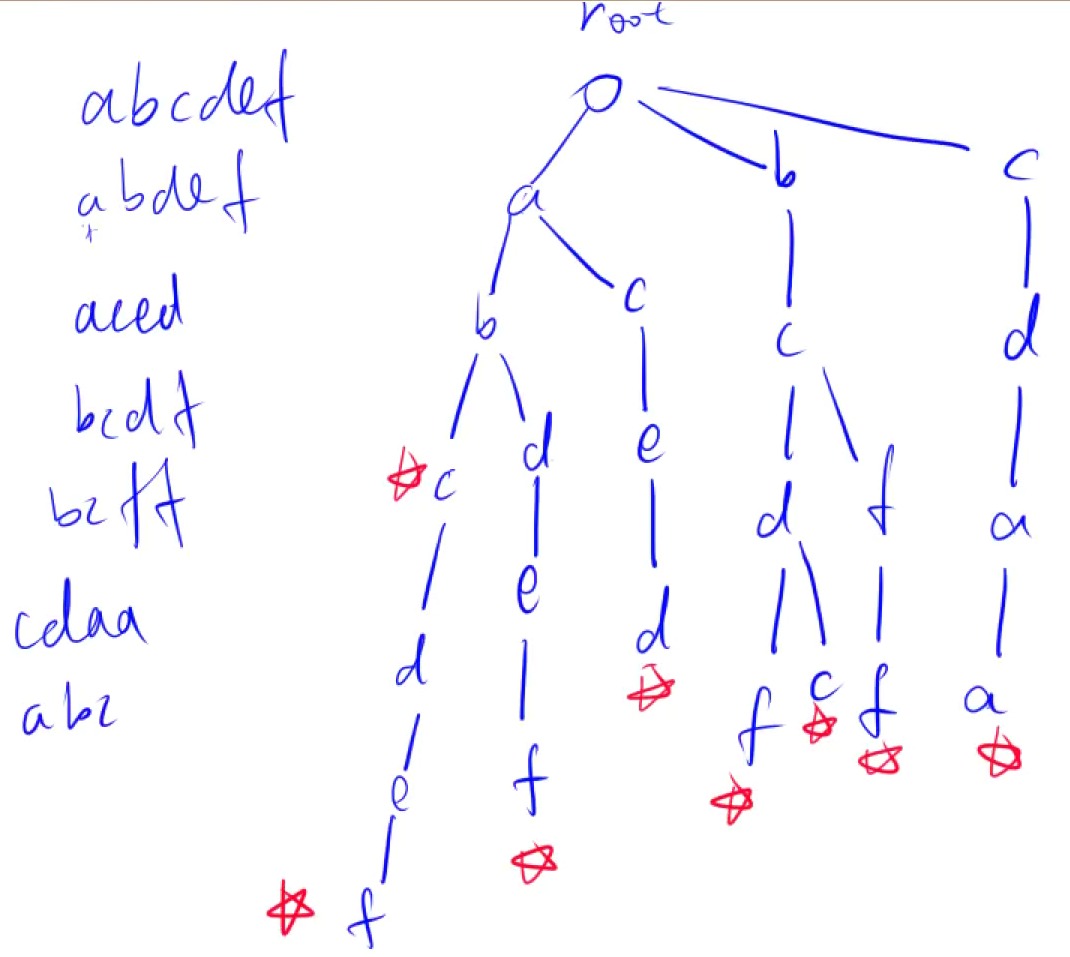
二、Trie树的应用

Trie字符串统计

题目描述：
维护一个字符串集合，支持两种操作：

1. I x 向集合中插入一个字符串 $x$；
2. Q x 询问一个字符串在集合中出现了多少次。

共有 $n$ 个操作，所有输入的字符串总长度不超过 $10^5$，字符串仅包含小写英文字母。

输入格式：
第一行包含整数 $n$，表示操作数。

接下来 $n$ 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式：
对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围：
$1\le n\le 2\ast 10^4$

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

代码实现：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int son[N][26], cnt[N], idx; // 因为题目仅包含小写英文字母 列设置为26

void insert(string& s)
{
	int p = 0;
	for (int i = 0; i < s.size(); ++i)
	{
		int u = s[i] - 'a';
		if (!son[p][u]) son[p][u] = ++idx; // 检测节点是否创建，若无则创建节点
		p = son[p][u]; // 利用idx值移动到下个节点
	}
	cnt[p]++; // 在储存字符串之后的末尾打上标记
}
int query(string& s)
{
	int p = 0;
	for (int i = 0; i < s.size(); i++)
	{
		int u = s[i] - 'a';
		if (!son[p][u]) return 0;
		p = son[p][u];
	}
	return cnt[p];
}

int main()
{
	cin.tie(nullptr);
	int n;
	string s;
	cin >> n;
	while (n--)
	{
		char op;
		cin >> op;
		switch (op)
		{
		case 'I':
			cin >> s;
			insert(s); break;
		case 'Q':
			cin >> s;
			cout << query(s) << endl; break;
		default:
			cout << "Please enter seriously!" << endl;
		}
	}
	return 0;
}

最大异或对（难点）

题目描述：
在给定的 $n$ 个整数 $A_1，A_2\dots \dots A_n$ 中选出两个进行 $xor$（异或）运算，得到的结果最大是多少？

输入格式：
第一行输入一个整数 $n$。

第二行输入 $n$ 个整数 $A_1～A_n$。

输出格式：
输出一个整数表示答案。

数据范围：
$1\le n\le 10^5$
$0\le A_i<2^{31}$

输入样例：

3
1 2 3

输出样例：

3

暴力遍历法

在运行上会超时，但不失为一种最容易想到的思路。

代码实现：

const int N = 1e5 + 10;
int a[N];
int res;
int main()
{
	cin.tie(nullptr);
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i) cin >> a[i];

	for (int i = 0; i < n; ++i)
		for (int j = i + 1; j < n; ++j)
			res = max(res, a[i] ^ a[j]);
	cout << res << endl;
	return 0;
}

Trie树优化法

思路：

1、将整数解析为二进制数，即有符号整数，31位，就是0−30，按Trie树进行存储, 整数的Trie树存储。

2、每个数字的每一个二进制位，需要从高位到低位，即for (int i = 30; i >= 0; i--)，想像一下你在构一个Trie树，那么根root就是最高位，然后一路走到31位，就是最低位。

3、每个数字想要找到与自己形成最大异或值的另一个数字，我们现在已经把它们保存到Trie 树里了，那怎么找呢？什么样的两个数字才是最大异或值的对呢？就是每一位完全相反的就肯定是最大的异或对！那如果某一位相反的结点并不存在呢？这就是退而求其次的思路了，我们尽量从左到右找出与当前数字本位相反的路径，如果存在，就继续探索，如果不存在，那就使用一样的本位值。这样下来，到31位，就可以找到和自己匹配最大的异或值。

代码实现：

这里可以采用两种方式使用Trie树：

1. 边插入边查询
2. 全部插入再查询

边插入边查询：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
const int M = N * 31;
int son[N][2], idx, a[N];

void insert(int x)
{
	int p = 0;
	for (int i = 30; i >= 0; --i)
	{
		int u = (x >> i) & 1;
		if (!son[p][u]) son[p][u] = ++idx;
		p = son[p][u];
	}
}

int query(int x)
{
	int p = 0, ans = 0;
	for (int i = 30; i >= 0; --i)
	{
		int u = (x >> i) & 1;
		if (son[p][!u])
		{
			p = son[p][!u];
			ans = ans * 2 + !u;
		}
		else
		{
			p = son[p][u];
			ans = ans * 2 + u;
		}
	}
	return ans;
}

int main()
{
	cin.tie(nullptr);
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i) cin >> a[i];
	int res = 0;
	for (int i = 0; i < n; i++)
	{
		insert(a[i]);
		int t = query(a[i]);
		res = max(res, a[i] ^ t);
	}
	cout << res << endl;
	return 0;
}

全部插入再查询：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
const int M = N * 31;
int son[N][2], idx, a[N];

void insert(int x)
{
	int p = 0;
	for (int i = 30; i >= 0; --i)
	{
		int u = (x >> i) & 1;
		if (!son[p][u]) son[p][u] = ++idx;
		p = son[p][u];
	}
}

int query(int x)
{
	int p = 0, ans = 0;
	for (int i = 30; i >= 0; --i)
	{
		int u = (x >> i) & 1;
		if (son[p][!u])
		{
			p = son[p][!u];
			ans = ans * 2 + !u;
		}
		else
		{
			p = son[p][u];
			ans = ans * 2 + u;
		}
	}
	return ans;
}

int main()
{
	cin.tie(nullptr);
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i) cin >> a[i], insert(a[i]);
	int res = 0;
	for (int i = 0; i < n; i++)
	{
		int t = query(a[i]);
		res = max(res, a[i] ^ t);
	}
	cout << res << endl;
	return 0;
}