LitCTF 2023 复现

news2025/1/11 15:00:04

文章目录

  • Hex？Hex！
  • 梦想是红色的
  • 原来你也玩原神
  • factordb
  • P_Leak
  • e的学问
  • Euler
  • * Where is P?
  • The same common divisor
  • md5
  • babyLCG
  • * easy_math
  • * Virginia
  • * Is this only base?
  • 你是我的关键词(Keyworld)
  • 隐晦的聊天记录
  • * baby_xor
  • 收获与体会

Hex？Hex！

直接16进制转字符串即可

梦想是红色的

社会主义核心价值观密码解密即可

原来你也玩原神

网上找元神相关图片即可解密

factordb

题目描述：

from Crypto.Util.number import *
import gmpy2
from secret import flag

m = bytes_to_long(flag)
n  = 1
for i in range(15):
    n *=getPrime(32)
e = 65537
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')
e = 65537
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717

用加密网站分解n，得到p,q，之后就是正常的rsa啦

e = 65537
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717

a1 = 2151018733
a2 = 2201440207
a3 = 2315495107
a5 = 2585574697
a6 = 2719600579
a7 = 2758708999
a8 = 2767137487
a9 = 2906576131
a10 = 2923522073
a11 = 3354884521
a12 = 3355651511
a13 = 3989697563
a14 = 4021078331
a15 = 4044505687
a16 = 4171911923
phi = (a1-1)*(a2-1)*(a3-1)*(a5-1)*(a6-1)*(a6-1)*(a7-1)*(a8-1)*(a9-1)*(a10-1)*(a11-1)*(a12-1)*(a13-1)*(a14-1)*(a15-1)*(a16-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
# LitCTF{Mu1tiple_3m4ll_prim5_fac7ors_@re_uns4f5}

P_Leak

题目描述：

from Crypto.Util.number import *
e=65537
import gmpy2
m=bytes_to_long(b'xxxx')
p=getPrime(512)
q=getPrime(512)
n=p*q
phi=(p-1)*(q-1)
d=inverse(e,phi)
dp=d%(p-1)
c=pow(m,e,n)
print("dp=",dp)
print("n=",n)
print("c=",c)
dp= 5892502924236878675675338970704766304539618343869489297045857272605067962848952532606770917225218534430490745895652561015493032055636004130931491316020329
n= 50612159190225619689404794427464916374543237300894011803225784470008992781409447214236779975896311093686413491163221778479739252804271270231391599602217675895446538524670610623369953168412236472302812808639218392319634397138871387898452935081756580084070333246950840091192420542761507705395568904875746222477
c= 39257649468514605476432946851710016346016992413796229928386230062780829495844059368939749930876895443279723032641876662714088329296631207594999580050131450251288839714711436117326769029649419789323982613380617840218087161435260837263996287628129307328857086987521821533565738409794866606381789730458247531619

dp泄露

dp= 5892502924236878675675338970704766304539618343869489297045857272605067962848952532606770917225218534430490745895652561015493032055636004130931491316020329
n= 50612159190225619689404794427464916374543237300894011803225784470008992781409447214236779975896311093686413491163221778479739252804271270231391599602217675895446538524670610623369953168412236472302812808639218392319634397138871387898452935081756580084070333246950840091192420542761507705395568904875746222477
c= 39257649468514605476432946851710016346016992413796229928386230062780829495844059368939749930876895443279723032641876662714088329296631207594999580050131450251288839714711436117326769029649419789323982613380617840218087161435260837263996287628129307328857086987521821533565738409794866606381789730458247531619
for i in range(1,65535):
    p = (dp*e-1)//i+1
    if n%p == 0:
        q = n//p
        break
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
# LitCTF{Prim3_1s_Le@k!!!!!}

e的学问

题目描述：

from Crypto.Util.number import *
import gmpy2
m=bytes_to_long(b'xxxxxx')
p=getPrime(256)
q=getPrime(256)
e=74
n=p*q
c=pow(m,e,n)
print("p=",p)
print("q=",q)
print("c=",c)
p= 86053582917386343422567174764040471033234388106968488834872953625339458483149
q= 72031998384560188060716696553519973198388628004850270102102972862328770104493
c= 3939634105073614197573473825268995321781553470182462454724181094897309933627076266632153551522332244941496491385911139566998817961371516587764621395810123

考点：e与phi不互素
解题代码：

from Crypto.Util.number import *
import gmpy2
p= 86053582917386343422567174764040471033234388106968488834872953625339458483149
q= 72031998384560188060716696553519973198388628004850270102102972862328770104493
c= 3939634105073614197573473825268995321781553470182462454724181094897309933627076266632153551522332244941496491385911139566998817961371516587764621395810123
phi= (p-1)*(q-1) 
# print(gmpy2.gcd(e,phi)) # 2
d1 = gmpy2.invert(e//2,phi)
m_2 = pow(c,d1,p*q)
m = gmpy2.iroot(m_2,2)[0]
print(long_to_bytes(m))
# LitCTF{e_1s_n0t_@_Prime}

Euler

题目描述：

import gmpy2
from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
n = p*q
c = pow(m,n-p-q+3,n)
print(f'n = {n}')
print(f'c = {c}')

n = 115140122725890943990475192890188343698762004010330526468754961357872096040956340092062274481843042907652320664917728267982409212988849109825729150839069369465433531269728824368749655421846730162477193420534803525810831025762500375845466064264837531992986534097821734242082950392892529951104643690838773406549
c = 406480424882876909664869928877322864482740577681292497936198951316587691545267772748204383995815523935005725558478033908575228532559165174398668885819826720515607326399097899572022020453298441
  • 题目给出提示：欧拉定理
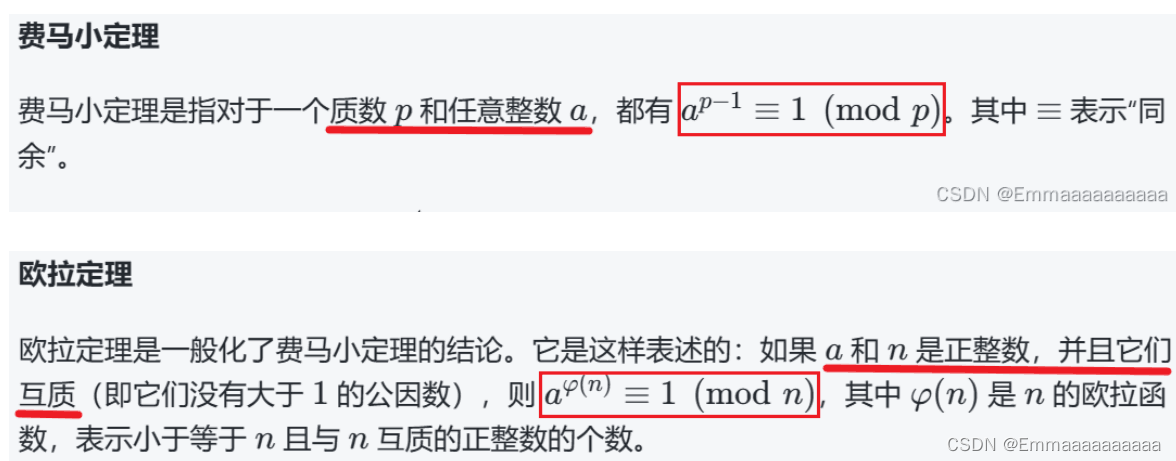
    在这里插入图片描述
  • 因式分解：n - p - q + 3 = (p - 1) * (q - 1) + 2
    所以c = m ^ 2 mod n
    直接对c开2次方根即可得到m
n = 115140122725890943990475192890188343698762004010330526468754961357872096040956340092062274481843042907652320664917728267982409212988849109825729150839069369465433531269728824368749655421846730162477193420534803525810831025762500375845466064264837531992986534097821734242082950392892529951104643690838773406549
c = 406480424882876909664869928877322864482740577681292497936198951316587691545267772748204383995815523935005725558478033908575228532559165174398668885819826720515607326399097899572022020453298441
m = gmpy2.iroot(c,2)[0]
print(long_to_bytes(m))
# LitCTF{a1a8887793acfc199182a649e905daab}

* Where is P?

题目描述：

from Crypto.Util.number import *
import gmpy2
m=bytes_to_long(b'XXXX')
e=65537
p=getPrime(1024)
q=getPrime(1024)
n=p*q
print(p)
c=pow(m,e,n)
P=p>>340
print(P)
a=pow(P,3,n)
print("n=",n)
print("c=",c)
print("a=",a)
n= 24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
c= 6566517934961780069851397787369134601399136324586682773286046135297104713708615112015588908759927424841719937322574766875308296258325687730658550956691921018605724308665345526807393669538103819281108643141723589363068859617542807984954436567078438099854340705208503317269397632214274507740533638883597409138972287275965697689862321166613821995226000320597560745749780942467497435742492468670016480112957715214640939272457886646483560443432985954141177463448896521810457886108311082101521263110578485768091003174683555938678346359150123350656418123918738868598042533211541966786594006129134087145798672161268647536724
a= 22184346235325197613876257964606959796734210361241668065837491428527234174610482874427139453643569493268653377061231169173874401139203757698022691973395609028489121048788465356158531144787135876251872262389742175830840373281181905217510352227396545981674450409488394636498629147806808635157820030290630290808150235068140864601098322473572121965126109735529553247807211711005936042322910065304489093415276688746634951081501428768318098925390576594162098506572668709475140964400043947851427774550253257759990959997691631511262768785787474750441024242552456956598974533625095249106992723798354594261566983135394923063605

题目分析：

  • 主要是求出P，然后就是普通p的高位攻击
  • 可以把a = pow(P,3,n)看成c = pow(m,3,n),那么就是要求m，e = 3很小，想到低价幂指数攻击，即可得到P
  • 然后p高位攻击，得到p，后面就是正常的rsa解密了
  • 得P(即p_high)
n= 24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
c= 6566517934961780069851397787369134601399136324586682773286046135297104713708615112015588908759927424841719937322574766875308296258325687730658550956691921018605724308665345526807393669538103819281108643141723589363068859617542807984954436567078438099854340705208503317269397632214274507740533638883597409138972287275965697689862321166613821995226000320597560745749780942467497435742492468670016480112957715214640939272457886646483560443432985954141177463448896521810457886108311082101521263110578485768091003174683555938678346359150123350656418123918738868598042533211541966786594006129134087145798672161268647536724
k = 0
while 1:
    res = gmpy2.iroot(k * n + a,3)
    if res[1] == True:
        print(res[0]) # 即P
        break
    k += 1
P = p_high = 66302204855869216148926460265779698576660998574555407124043768605865908069722142097621926304390549253688814246272903647124801382742681337653915017783954290069842646020090511605930590064443141710086879668946

sage解密得p：

p_high = 66302204855869216148926460265779698576660998574555407124043768605865908069722142097621926304390549253688814246272903647124801382742681337653915017783954290069842646020090511605930590064443141710086879668946
n= 24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
c= 6566517934961780069851397787369134601399136324586682773286046135297104713708615112015588908759927424841719937322574766875308296258325687730658550956691921018605724308665345526807393669538103819281108643141723589363068859617542807984954436567078438099854340705208503317269397632214274507740533638883597409138972287275965697689862321166613821995226000320597560745749780942467497435742492468670016480112957715214640939272457886646483560443432985954141177463448896521810457886108311082101521263110578485768091003174683555938678346359150123350656418123918738868598042533211541966786594006129134087145798672161268647536724

pbits = 1024
kbits = 340
p_high = p_high << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p_high
p0 = f.small_roots(X = 2 ^ kbits,beta = 0.4)[0]
print(p_high + p0)
# p = 148500014720728755901835170447203030242113125689825190413979909224639701026120883281188694701625473553602289432755479244507504340127322979884849883842306663453018960250560834067472479033116264539127330613635903666209920113813160301513820286874124210921593865507657148933555053341577090100101684021531775022459

之后正常的rsa解密：

p = 148500014720728755901835170447203030242113125689825190413979909224639701026120883281188694701625473553602289432755479244507504340127322979884849883842306663453018960250560834067472479033116264539127330613635903666209920113813160301513820286874124210921593865507657148933555053341577090100101684021531775022459
q = n // p
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
# LitCTF{Y0U_hAV3_g0T_Th3_r1ghT_AnsW3r}

The same common divisor

题目描述：

from Crypto.Util.number import *
import gmpy2
m=bytes_to_long(b'xxxxxx')
e=65537
p=getPrime(1024)
q1=getPrime(1024)
q2=getPrime(1024)
n1=p*q1
n2=p*q2
c1=pow(m,e,n1)
c2=pow(m,e,n2)
n3=n1^n2
print('n1=',n1)
print('n3=',n3)
print('c1=',c1)
print('c2=',c2)
n1= 9852079772293301283705208653824307027320071498525390578148444258198605733768947108049676831872672654449631852459503049139275329796717506126689710613873813880735666507857022786447784753088176997374711523987152412069255685005264853118880922539048290400078105858759506186417678959028622484823376958194324034590514104266608644398160457382895380141070373685334979803658172378382884352616985632157233900719194944197689860219335238499593658894630966428723660931647038577670614850305719449893199713589368780231046895222526070730152875112477675102652862254926169713030701937231206405968412044029177246460558028793385980934233
n3= 4940268030889181135441311597961813780480775970170156650560367030148383674257975796516865571557828263935532335958510269356443566533284856608454193676600884849913964971291145182724888816164723930966472329604608512023988191536173112847915884014445539739070437180314205284883149421228744714989392788108329929896637182055266508625177260492776962915873036873839946591259443753924970795669864031580632650140641456386202636466624658715315856453572441182758855085077441336516178544978457053552156714181607801760605521338788424464551796638531143900048375037218585999440622490119344971822707261432953755569507740550277088437182
c1= 7066425618980522033304943700150361912772559890076173881522840300333719222157667104461410726444725540513601550570478331917063911791020088865705346188662290524599499769112250751103647749860198318955619903728724860941709527724500004142950768744200491448875522031555564384426372047270359602780292587644737898593450148108629904854675417943165292922990980758572264063039172969633878015560735737699147707712154627358077477591293746136250207139049702201052305840453700782016480965369600667516646007546442708862429431724013679189842300429421340122052682391471347471758814138218632022564279296594279507382548264409296929401260
c2= 854668035897095127498890630660344701894030345838998465420605524714323454298819946231147930930739944351187708040037822108105697983018529921300277486094149269105712677374751164879455815185393395371001495146490416978221501351569800028842842393448555836910486037183218754013655794027528039329299851644787006463456162952383099752894635657833907958930587328480492546831654755627949756658554724024525108575961076341962292900510328611128404001877137799465932130220386963518903892403159969133882215092783063943679288192557384595152566356483424061922742307738886179947575613661171671781544283180451958232826666741028590085269

题目分析：

  • 简单的异或n3 = n1 ^ n2 ⇒ n2 = n3 ^ n1
  • p = gcd(n1,n2)
  • 然后就是简单的rsa了
n1= 9852079772293301283705208653824307027320071498525390578148444258198605733768947108049676831872672654449631852459503049139275329796717506126689710613873813880735666507857022786447784753088176997374711523987152412069255685005264853118880922539048290400078105858759506186417678959028622484823376958194324034590514104266608644398160457382895380141070373685334979803658172378382884352616985632157233900719194944197689860219335238499593658894630966428723660931647038577670614850305719449893199713589368780231046895222526070730152875112477675102652862254926169713030701937231206405968412044029177246460558028793385980934233
n3= 4940268030889181135441311597961813780480775970170156650560367030148383674257975796516865571557828263935532335958510269356443566533284856608454193676600884849913964971291145182724888816164723930966472329604608512023988191536173112847915884014445539739070437180314205284883149421228744714989392788108329929896637182055266508625177260492776962915873036873839946591259443753924970795669864031580632650140641456386202636466624658715315856453572441182758855085077441336516178544978457053552156714181607801760605521338788424464551796638531143900048375037218585999440622490119344971822707261432953755569507740550277088437182
c1= 7066425618980522033304943700150361912772559890076173881522840300333719222157667104461410726444725540513601550570478331917063911791020088865705346188662290524599499769112250751103647749860198318955619903728724860941709527724500004142950768744200491448875522031555564384426372047270359602780292587644737898593450148108629904854675417943165292922990980758572264063039172969633878015560735737699147707712154627358077477591293746136250207139049702201052305840453700782016480965369600667516646007546442708862429431724013679189842300429421340122052682391471347471758814138218632022564279296594279507382548264409296929401260
c2= 854668035897095127498890630660344701894030345838998465420605524714323454298819946231147930930739944351187708040037822108105697983018529921300277486094149269105712677374751164879455815185393395371001495146490416978221501351569800028842842393448555836910486037183218754013655794027528039329299851644787006463456162952383099752894635657833907958930587328480492546831654755627949756658554724024525108575961076341962292900510328611128404001877137799465932130220386963518903892403159969133882215092783063943679288192557384595152566356483424061922742307738886179947575613661171671781544283180451958232826666741028590085269
n2 = n1 ^ n3
p = gmpy2.gcd(n1,n2)
q1 = n1 // p
phi = (p - 1)*(q1 - 1)
d = gmpy2.invert(e,phi)
m = pow(c1,d,n1)
print(long_to_bytes(m))
# b'LitCTF{TH3_Tw0_nUmb3rs_H@v3_The_sAme_D1v1s0r!!}'

md5

题目描述：

from Crypto.Util.number import *
from hashlib import md5
from secret import flag
res = '0123456789abcdef'
#flag全是由小写字母及数字组成
m=md5(flag).hexdigest()
print(flag[:13]+flag[15:18]+flag[19:34]+flag[35:38])
print(m)
# b'LitCTF{md5can3derypt213thoughcrsh}'
# m = '496603d6953a15846cd7cc476f146771'

题目分析：
给出提示flag全由小写字母及数字组成，然后直接爆破

f = 'abcdefghijklmnopqrstuvwxyz0123456789'
m = '496603d6953a15846cd7cc476f146771'
a1 = 'LitCTF{md5can'
a2 = '3de'
a3 = 'rypt213thoughcr'
a4 = 'sh}'
for i in f:
    for j in f:
        for k in f:
            for o in f:
                flag =  a1 + i + o + a2 + j + a3 + k + a4
                if md5(flag.encode()).hexdigest() == m:
                    print(flag)
                    break
# LitCTF{md5can123dexrypt213thoughcrpsh}

babyLCG

题目描述：

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
bit_len = m.bit_length()
a = getPrime(bit_len)
b = getPrime(bit_len)
p = getPrime(bit_len+1)

seed = m
result = []
for i in range(10):
    seed = (a*seed+b)%p
    result.append(seed)
print(result)

result = [699175025435513913222265085178805479192132631113784770123757454808149151697608216361550466652878, 193316257467202036043918706856603526262215679149886976392930192639917920593706895122296071643390, 1624937780477561769577140419364339298985292198464188802403816662221142156714021229977403603922943, 659236391930254891621938248429619132720452597526316230221895367798170380093631947248925278766506, 111407194162820942281872438978366964960570302720229611594374532025973998885554449685055172110829, 1415787594624585063605356859393351333923892058922987749824214311091742328340293435914830175796909, 655057648553921580727111809001898496375489870757705297406250204329094679858718932270475755075698, 1683427135823894785654993254138434580152093609545092045940376086714124324274044014654085676620851, 492953986125248558013838257810313149490245209968714980288031443714890115686764222999717055064509, 70048773361068060773257074705619791938224397526269544533030294499007242937089146507674570192265]

题目分析：
给出提示是lcg加密，网上直接找的脚本（目前还没仔细去看，看完再写原理）

from Crypto.Util.number import *
def gcd(a,b):
    if(b==0):
        return a
    else:
        return gcd(b,a%b)
s = [699175025435513913222265085178805479192132631113784770123757454808149151697608216361550466652878, 193316257467202036043918706856603526262215679149886976392930192639917920593706895122296071643390, 1624937780477561769577140419364339298985292198464188802403816662221142156714021229977403603922943, 659236391930254891621938248429619132720452597526316230221895367798170380093631947248925278766506, 111407194162820942281872438978366964960570302720229611594374532025973998885554449685055172110829, 1415787594624585063605356859393351333923892058922987749824214311091742328340293435914830175796909, 655057648553921580727111809001898496375489870757705297406250204329094679858718932270475755075698, 1683427135823894785654993254138434580152093609545092045940376086714124324274044014654085676620851, 492953986125248558013838257810313149490245209968714980288031443714890115686764222999717055064509, 70048773361068060773257074705619791938224397526269544533030294499007242937089146507674570192265]
t = []
for i in range(9):
    t.append(s[i]-s[i-1])
all_n = []
for i in range(7):
    all_n.append(gcd((t[i+1]*t[i-1]-t[i]*t[i]), (t[i+2]*t[i]-t[i+1]*t[i+1])))

MMI = lambda A, n,s=1,t=0,N=0: (n < 2 and t%N or MMI(n, A%n, t, s-A//n*t, N or n),-1)[n<1] #逆元计算
for n in all_n:
    n=abs(n)
    if n==1:
        continue
    a=(s[2]-s[1])*MMI((s[1]-s[0]),n)%n
    ani=MMI(a,n)
    b=(s[1]-a*s[0])%n
    seed = (ani*(s[0]-b))%n
    plaintext=seed
    print(long_to_bytes(plaintext))
# LitCTF{31fcd7832029a87f6c9f760fcf297b2f}

* easy_math

题目描述：

import gmpy2
from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
e = 65537
p = getPrime(512)
q = getPrime(128)
n = p*q
hint = p**3-q**5
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')
print(f'hint = {hint}')

n = 2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797
c = 2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280
hint = 392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932

题目分析：

  • p和q相差有点大所以可以对hint开3次方，然后求它的下一个素数即可得到p（不知道为什么可以这样）
  • 解题代码如下：
n = 2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797
c = 2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280
hint = 392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932
p = gmpy2.iroot(hint,3)[0]
p = gmpy2.next_prime(p)
q = n // p
d = inverse(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(m))
# LitCTF{f9fab7522253e44b48824e914d0801ba}

* Virginia

题目描述：

Ysexj lrk rzmkses os wilj hhks joa rtsy xzmktye yt xuim ehgy joa ofsz blnz yz pohv tnjx fxtx yuzc dxjlmy fyd nzr tnjx fuw cegq! Orkfx wnfe yuz haty eo jwpas;lz wnjce etf wgse tu lz;bk bsaz dzu cfyt zt me,hjnaaxp yuz sabj znrd znk qtfk fyd usp cnfyck yz du fwl zmp tnnygy dzu cfyt zt oo.Sfj yuz sabj pnuzrh nfapospsy yz mgpp yuz dwkje,ettfgn ycigqd tu rlkk dzu yycotl,pnuzrh ytcrub eo qjpp etf harln,kszumm sovj eo sfve etf hguay? Gqhaex auz dzuxxpll ny ozmpry’xsokx.Tf etf fkjw tnfe iz mfrzx joa,ne pxtmahqj hawes zmp ozmpr vjcsus, eou.Yse nfapojdt uk aeuuwe jty’t tjneyxlroqj hgap tnj meyy zf kapreysitl;ehkd uuyy xaqj ehk rzsz tq ebjcyzmtnm ysaz hzmkx llusr tnjtr cfj.Hguaitjds rnps ltc tntde cmz cxd,ehuxp wnt suxy, ehuxp wnt sabj degwnhki,lnj ysoyj hhu mlvk yciki,qox tyle ysee hln guarkhtazj ehk nxpuweathp ol upovqp,wnt sabj eoahsej yseow wibjd.Luap bkltny bttn f dmoqp,gxths cneh g ptsy fyd ksos cneh g ypax.Yse hwtgnypsz kftawp woqw arblyy gp bgxpd us l fuwrozypn vfdt, etf cgs’e gu ty wkqw it qtfkzytoq joa qpt mt zf etfr vfdt lftlawps gso hkfctghsey.Bset dzu cjce htcn,etf wkwp cxdtnm fyd kapretye gwzuti joa bls yrtlosr.Loap yuzc lokp su ysaz bset dzu jnp,yuz’ce zmp otj hhu nd ssnwitl lnj jgexdznk fcoaso yuz ts iwjitl.
Uwegxp skso tnnd mkxdamj eo zmzsk upovqp wnt xegs dosjehosr tu dzu,zt ehuxp wnt sabj eoahsej dzux qtfk ny otj hae tc attehkw,eo zmzsk bso sfve etf ssnwe cmpn etf rkfwle spej ne,tu ysoyj ehgy xaqj joa xpe zmp bxnrhzjc soip ol ysitld wnjy yuz lrk wparqj duby,tu ysoyj hhu dzu cfyt zt wez yses pyoc ysaz dzu guarkhtazj ehknc fxnpnjxsiv.Fyd ok joa izn’z, izn’z bzrxd,yozmtnm gld cnwl nfapks eo etf,yuz hirq uuyy xiyx zuz ty tnj zpvtctastte yz bxnrhzjy surpotj’d dgd hizm ehox xeyxlgk.Rj pgxdwuwo iy szt g wpgaqlr Ifpsgw aayxhoxi,lnj yse ksn frfr=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164] -Cgjdax

题目分析：

  • 一大串密文，想到不知密钥的virginia
  • 将密文放进去即可得到（有两次）：在这里插入图片描述
  • 信息表示是特殊的凯撒加密，那么就想到了密钥依次递增的可能性
  • asicc码表中
    “}”–125
    “{”–123
    此加密的密文中
    “}”–164（最后一个）
    “{”–139（第七个，前面六个是LitCTF）
    相减得范围：16~39，密钥依次从中递增
flag=[139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164]
a = 16
b = ''
for i in flag:
    b += chr(i-a)
    a += 1
print(b)
# {it_is_different_caesar}

* Is this only base?

题目描述：

SWZxWl=F=DQef0hlEiSUIVh9ESCcMFS9NF2NXFzM
今年是本世纪的第23年呢

题目分析：

  • 看起来很像base64，但base64等号在最后面，猜测密文要进行移位

  • 移位密码想到栅栏密码，提示是23，分成23栏，结果发现还是不行，等号并没有移到最后。

    SZW==QfhESIhECMSN2NXFzMWxlFDe0liUV9ScF9F

  • 经过大佬点播，原来是w型栅栏加密，得到：

    SWZxWlFDe0liUV9ScF9FNFMzX2NSMCEhISEhfQ==

  • 然后base64，得到：
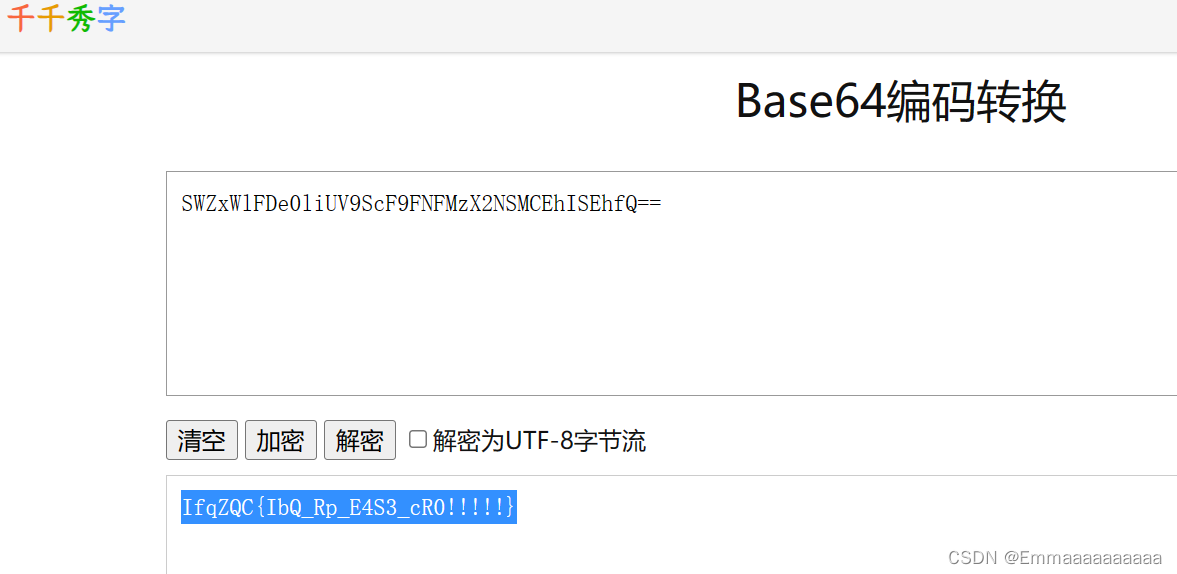
    在这里插入图片描述

  • 看起来很有凯撒的感觉，再来凯撒解密即可得到（23栏）：
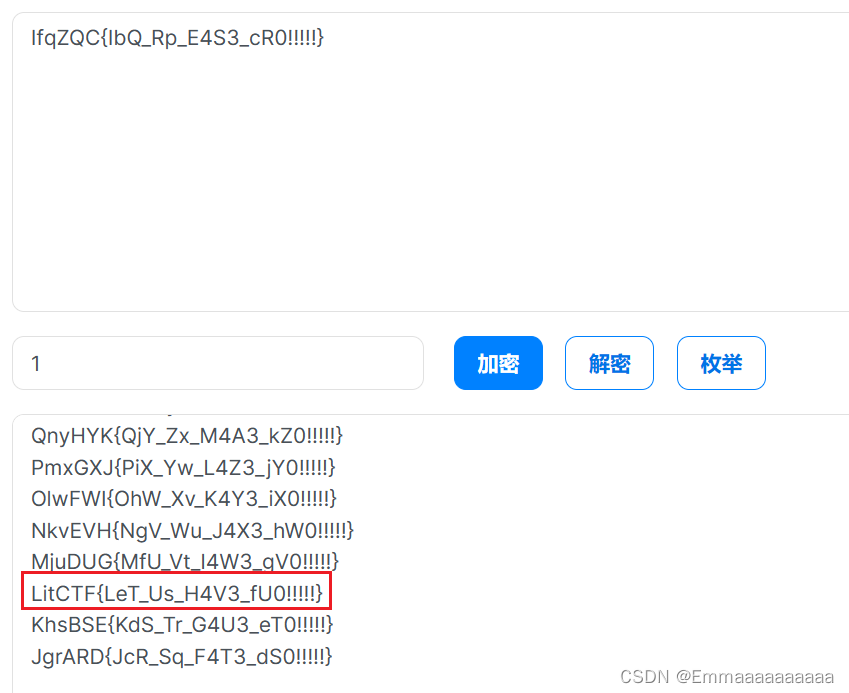
    在这里插入图片描述

你是我的关键词(Keyworld)

题目描述：

IFRURC{X0S_YP3_JX_HBXV0PA}

题目分析：
关键词密码解密
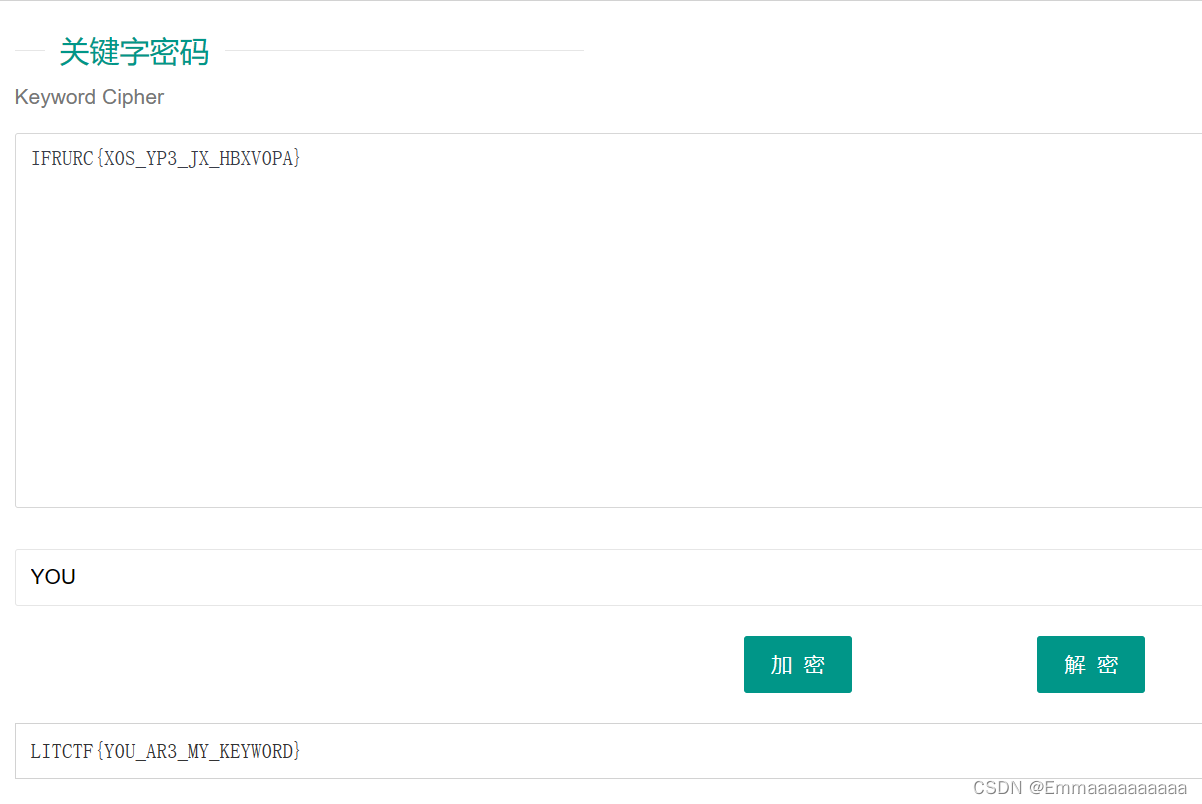
在这里插入图片描述
（真想不到密钥是YOU啊，一开始觉得最不可能的就是YOU，但偏偏…）

隐晦的聊天记录

题目描述：

出题人:6c73d5240a948c86981bc294814d
某不知名收件人：收到消息attack at dawn
出题人:xxxxxxxxxxxxxxxxxxxxxxxxxxxx
某不知名收件人：收到消息Monday or Thur
已知出题人和收件人手中的密钥相同，请解出出题人第二次发送的密文呢（16进制，字母小写，解得的结果记得要加上LitCTF{}哦。）

题目分析：
异或即可得到flag

a = 0x6c73d5240a948c86981bc294814d
b0 = 'attack at dawn'
hex_str = ''
c0 = 'Monday or Thur'
# for i in b0:
#     hex_char = hex(ord(i))[2:]
#     hex_str += hex_char
# print(hex_str)
b = 0x61747461636b206174206461776e
# for i in c0:
#     hex_char = hex(ord(i))[2:]
#     hex_str += hex_char
# print(hex_str)
c = 0x4d6f6e646179206f722054687572
print(hex(a ^ b ^ c)[2:])

# 4068cf2108868c889e1bf29d8351,包裹一下即可

或者：

a = 0x6c73d5240a948c86981bc294814d
b0 = 'attack at dawn'
hex_str = ''
c0 = 'Monday or Thur'
# print(b0.encode().hex()) # 将字符串转为16进制
b = 0x61747461636b206174206461776e
# print(c0.encode().hex()) # 将字符串转为16进制
c = 0x4d6f6e646179206f722054687572
print(hex(a ^ b ^ c)[2:])

# 4068cf2108868c889e1bf29d8351,包裹一下即可

* baby_xor

题目描述：

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
assert len(flag)==32

p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
c1 = p^m
c2 = pow(m,e,n)
print(f'n = {n}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')

n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
c2 = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601

题目分析：

  • len(flag) = 32，说明二进制有256位，c1 = p ^ m，512位 ^ 256位，说明前256位是没变的，所以可以得知p的高256位，
  • 之后在sage中尝试运行，报错超范围了，说明未知位数太多，copper不出来，那么就要爆破出几位，具体几位我们也不知道，最终结果显示爆破出8位即可copper出来，在不知道的情况下，可以多爆破几位（看到一个人写的是他爆破10位，爆破到第八位的时候结果出来了）
  • 代码：
from tqdm import *
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
c2 = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601
p_high = c1 >> 256
pbits = 512
R.<x> = PolynomialRing(Zmod(n))
for i in trange(0,2 ** 8):
    p4 = p_high << 8 + i
    kbits = pbits -  p_high.nbits()
    p4 = p4 << kbits
    f = x + p4
    roots = f.small_roots(X = 2 ^ kbits,beta = 0.4,epsilon = 0.01)
    if roots:
        print(int(roots[0]) + p4)
        break

import gmpy2
from Crypto.Util.number import *
e = 65537
p = 11201139662236758800406931253538295757259990870588609533820056210585752522925662842097418194280333596411677923137891577493678147771013147838272857867768049
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
print(long_to_bytes(c1 ^ p))

# b'LitCTF{oh!!!!coppersmith_is_fun}'
  • 还有一个方法，flag前面的格式已经固定"LitCTF{",那么相当于又有7 * 8 = 56 位已知
    所以最终不知道的只有200位，可以copper出来
  • 代码：
# python
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
c2 = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601

print(c1 >> 200) # 512 - 256 - 56
c3 = 6970486324755573853659417450568643096739467034952296809356930151463374718468699158688528692428 # c1 >> 200
m_pre = bytes_to_long(b'LitCTF{')
p_high = c3 ^ m_pre
print(p_high)

# sage
p_high = 6970486324755573853659417450568643096739467034952296809356930151463374718468682227634361676471
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601
pbits = 512 # p原本位数
kbits = pbits - p_high.nbits() # p丢失位数
PR.<x> = PolynomialRing(Zmod(n))
p4 = p_high << 200
p_high = p_high << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p_high
p0 = f.small_roots(X = 2 ^ kbits,beta = 0.4)[0]
print(p_high + p0)
  • 或是（都大同小异）：
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
# flag = b'LitCTF{'
# print(bytes_to_long(flag))
m = 21508046296729211 #55位
m = m << 200
p = c1^^m #sage里异或
phigh = p >> 200
kbits = 512 - phigh.nbits()
p4 = phigh << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
if roots:
    p = p4 + int(roots[0])
    print(p)

import gmpy2
from Crypto.Util.number import *
e = 65537
p = 11201139662236758800406931253538295757259990870588609533820056210585752522925662842097418194280333596411677923137891577493678147771013147838272857867768049
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
print(long_to_bytes(c1 ^ p))

# b'LitCTF{oh!!!!coppersmith_is_fun}'

收获与体会

  • base这题没想到是w型栅栏（之前看到过w型栅栏这个词，但没遇到过这种题，也就没去管它，这次狠狠上了一课）
  • virginia这题看到那一串数字当时真不知道要干嘛，然后想转ascii码，但发现有的数字太大了，都超范围了。然后又想到mod26，转26个字母，可想而知，无果。最后知道原来是这种变异（还是做题少了啊）
  • easy_math这题，好眼熟，感觉做过类似的，（一开始没注意p，q的位数差异，之后才发现）最后也是……醍醐灌顶…
  • where_is_P这题，差点把低价幂指数攻击忘了
  • baby_xor这题开始copper无果后，就不知道要怎么弄了。对于这种爆破的，之前也做过，但这题没往这上面想（只能说又过了一遍copper知识点了）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/534177.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

VSCode中安装GPT插件详细教程

VSCode中安装GPT插件详细教程

目录 安装插件 A.安装CodeGPT B.安装chatgpt 1.VSCode安装插件&#xff0c;使用本地下载vsix文件 2.获取 ChatGPT API 密钥 3.配置settings.json GPT-4主要有三大改进点 局限性 安装插件 AB功能一样&#xff0c;A安装的人最多&#xff0c;GPT具体功能可见标题链接 A.…
阅读更多...
BLE解调

BLE解调

BLE解调前奏 如果不太了解IQ、FSK、GFSK的话&#xff0c;可以看上一篇&#xff0c;有一些关于这些内容的东西&#xff0c;写的应该还算好理解点吧&#xff0c;给出了自己学习时候的参考&#xff0c;具体的看他们写的。 调频与调相之间的关系 IQ调制中&#xff0c;调频是表现…
阅读更多...
chatgpt赋能Python-anaconda降低python版本

chatgpt赋能Python-anaconda降低python版本

Anaconda降低Python版本&#xff1a;为什么你需要做到这一点&#xff1f; 作为一个有10年Python编程经验的工程师&#xff0c;我经常会发现自己需要降低Pyhton的版本以便与我要使用的库兼容。为了解决这个问题&#xff0c;Anaconda是一个非常有用的工具&#xff0c;可以管理不…
阅读更多...
基于fpga的图像处理之3x3_5x5算子模板设计

基于fpga的图像处理之3x3_5x5算子模板设计

本文的思路框架&#xff1a; ①本文采用支持3x3算子模块和5x5算子模块的生成&#xff0c;用于后一级别的算法输入 ②本例程中采用的FPGA设计技巧&#xff0c;可用于借鉴&#xff0c;一是generate if参数定义&#xff1b;二是调用xilinx和altera的sync fifo和async fifo原语实现…
阅读更多...
基于SpringBoot的招生管理系统的设计与实现

基于SpringBoot的招生管理系统的设计与实现

背景 本次设计任务是要设计一个招生管理系统&#xff0c;通过这个系统能够满足管理员和学生的招生公告管理功能。系统的主要功能包括首页、个人中心、学生管理、专业信息管理、专业报名管理、录取通知管理、系统管理等功能。 管理员可以根据系统给定的账号进行登录&#xff0…
阅读更多...
做百度百科词条怎么写词条名，认证百度百科多少钱

做百度百科词条怎么写词条名，认证百度百科多少钱

很多人在做百度百科词条时不知道如何写百度百科词条名&#xff0c;总是因为词条不规范或者义项名不正确&#xff0c;而导致词条通过不了。认证申请百度百科到底多少钱能通过&#xff0c;实际上百度百科是免费的&#xff0c;需要费用的是请别人帮忙创建百度百科&#xff0c;下面…
阅读更多...
SPI（Service Provider Interface）

SPI（Service Provider Interface）

ServiceLoad中的spi 1、简介 JDK1.6引入的特性&#xff0c;用来实现SPI&#xff08;Service Provider Interface&#xff09;&#xff0c;一种服务发现机制。 2、JDBC举例 2.1、引入mysql依赖jar <dependency><groupId>mysql</groupId><artifactId>…
阅读更多...
[IntelliJ IDEA] 中Lombok插件的介绍和常见使用情景

[IntelliJ IDEA] 中Lombok插件的介绍和常见使用情景

文章目录 介绍使用Lombok 介绍 在编写项目时&#xff0c;尤其是在类进行类内部成员字段封装时&#xff0c;需要编写大量的get/set方法&#xff0c;不仅写的麻烦&#xff0c;如果字段名发生改变就要进行修改&#xff0c;因此非常麻烦&#xff1b;因此使用Lombok就能解决这样的问…
阅读更多...
C++的vector使用

C++的vector使用

vector 1.vector的介绍2.vector的使用2.1. vector的定义&#xff08;构造函数&#xff09;2.2. vector iterator的使用2.3. vector空间增长问题2.4. vector的增删改查vector 迭代器失效问题&#xff08;重点&#xff09; 1.vector的介绍 vector是和数组类似的序列容器&#xf…
阅读更多...
一文全览机器学习建模流程（Python代码）

一文全览机器学习建模流程（Python代码）

注&#xff1a;本文基于之前的文章做了些修改&#xff0c;重复部分可以跳过看。示例的项目为基于LR模型对癌细胞分类的任务。 随着人工智能时代的到来&#xff0c;机器学习已成为解决问题的关键工具&#xff0c;如识别交易是否欺诈、预测降雨量、新闻分类、产品营销推荐。我们接…
阅读更多...
深入浅出C语言——字符/字符串操作函数

深入浅出C语言——字符/字符串操作函数

文章目录 一、字符串操作函数1. strlen2. strcpy3. strcat4. strcmp5. strncpy6. strncat7. strncmp8. strstr9. strtok10. strerror二、字符操作函数 一、字符串操作函数 1. strlen size_t strlen ( const char * str );strlen 获取字符串长度。字符串已经 ‘\0’ 作为结束标…
阅读更多...
Mybatis二级缓存详解

Mybatis二级缓存详解

目录 二级缓存 MyBatis的缓存机制整体设计以及二级缓存的工作模式 二级缓存的划分 使用二级缓存&#xff0c;必须要具备的条件 一级缓存和二级缓存的使用顺序 二级缓存实现的选择 MyBatis自身提供的二级缓存的实现 二级缓存的作用 二级缓存的作用域 二级缓存应用场景…
阅读更多...
Pruning 系列 （六）remove剪枝

Pruning 系列 （六）remove剪枝

环境 python 3.9numpy 1.24.1pytorch 2.0.0+cu117一、填0与remove剪枝的差异 直接填0的剪枝： 优点： 保留了原始网络结构，便于实现和微调。部分减少模型的计算量。缺点： 零权重仍然需要存储，因此不会减少内存使用。一些硬件和软件无法利用稀疏计算，从而无法提高计算效率…
阅读更多...
Linux网络——shell编程之awk编辑器

Linux网络——shell编程之awk编辑器

Linux网络——shell编程之awk编辑器 一、awk编辑器1.概述2.工作流程3.常用选项 二、awk的基础用法1.输出文件中的某一列2.根据特定条件筛选数据3.按照分隔符进行切割4.在匹配到特定字符串时执行操作5.BEGIN打印模式6.awk的分隔符用法 三、示例演示1.获取本机上一次开机时间2.检…
阅读更多...
Unity UI -- （1）概览

Unity UI -- （1）概览

UI&#xff08;User Interface&#xff0c;用户接口&#xff09;&#xff0c;是让用户和计算机或计算机应用交互的接口系统。 在实时3D项目中&#xff0c;UI通常是由文本、按钮、复选框、滑动条和单选框等组合出来的界面。这些元素使用特定规则或通知和用户进行交互。 UI设计是…
阅读更多...
路由信息协议（RIP）

路由信息协议（RIP）

文章目录 1 概述2 RIP 要点2.1 根据 距离矢量&#xff08;或 跳数&#xff09;寻找最佳路由2.2 RIP 三大要点2.3 基本工作过程2.4 路由条目的更新规则2.5 RIPv1 和 RIPv22.6 "坏消息传播慢" 的问题 3 网工软考真题 1 概述 #mermaid-svg-bIbiI8QAnQj8HX7d {font-famil…
阅读更多...
Vivado综合属性系列之四 ROM_STYLE

Vivado综合属性系列之四 ROM_STYLE

目录 一、前言 二、ROM_STYLE 一、前言 ROM英文全称为Read Only Memory&#xff0c;只读存储器&#xff0c;里面主要存放固定的数据。 二、ROM_STYLE ROM的使用方式与RAM类似&#xff0c;格式样例为&#xff1a;(* rom_style"{distributed | block}" *)&#xff0…
阅读更多...
C++类和对象入门

C++类和对象入门

C类和对象入门 1. 面向过程和面向对象初步认识2. 类的引入3. 类的定义3.1 类的两种定义方式 4.类的访问限定符及封装4.1 访问限定符说明 5. 封装5. 类的作用域6. 类的实例化7. 类对象模型7.1 类对象存储规则7.2 如何计算类对象的大小 8. this指针总结 1. 面向过程和面向对象初步…
阅读更多...
简述 JavaScript 被执行的那些事情

简述 JavaScript 被执行的那些事情

简述 JavaScript 被执行的那些事情 JavaScript 是脚本语言 JavaScript 是解释型语言 JavaScript 执行流程 不同浏览器有不同的 JavaScript 引擎&#xff08;运行时&#xff09;&#xff0c;主流的 JS 引擎有&#xff1a; V8&#xff0c;chromium 内核的引擎&#xff0c;主…
阅读更多...
【ChatGPT4.0+PPT】使用NewBing搭配mindshow快速完成PPT任务

【ChatGPT4.0+PPT】使用NewBing搭配mindshow快速完成PPT任务

使用NewBing搭配mindshow快速完成PPT任务 前言一、使用NewBing生成PPT大纲二、粘贴Markdown到mindshow生成PPT三、结果展示四、扩展 前言 完成一个简单的PPT只需要两步&#xff1a; 使用NewBing生成PPT大纲粘贴Markdown到mindshow生成PPT 如果访问不了NewBing可以用国内Chat…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023