最烧脑的悖论,意识为什么会影响未来?颠覆你认知的三门问题播报文章
小红虾实验室
2023-04-09 06:08
四川
好看视频优创联盟,优质科学领域创作者
关注
对于懂概率的人来说,他中大奖的概率将成倍增加,甚至获奖率能够达到100%。
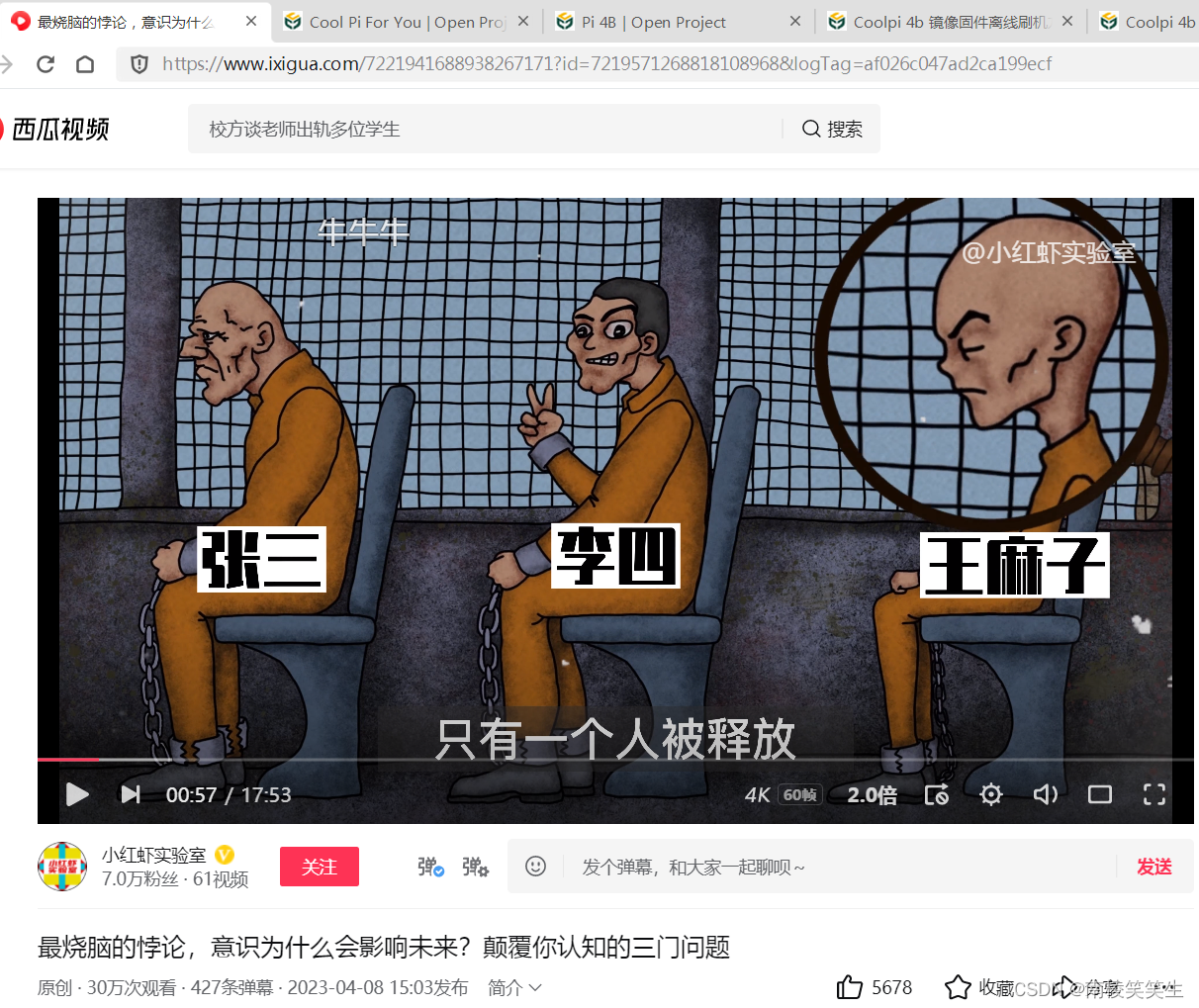
今天的内容足以颠覆你对世界的认知。在一道极为简单的数学问题上,98%的人都做了错误的选择。我们先从法外狂徒张三说起,张三落网后,和李四、王麻子关押在同一所天牢。恰逢新皇登基,大赦天下,要对一批死囚犯进行赦免。然而张三、李四、王麻子这三个死囚中,只能释放一个人,另外两个人将被处死。当消息传到天牢的时候,这三个人都喜出望外,因为都有被释放的一线可能。但在欢喜过后,又是无尽的恐怖,他们不知道谁会被释放。法外狂徒张三的大脑在飞速的运转,他便跟看守套近乎,欲获得情报。可是看守根本就不吃这一套,半个字都没说。
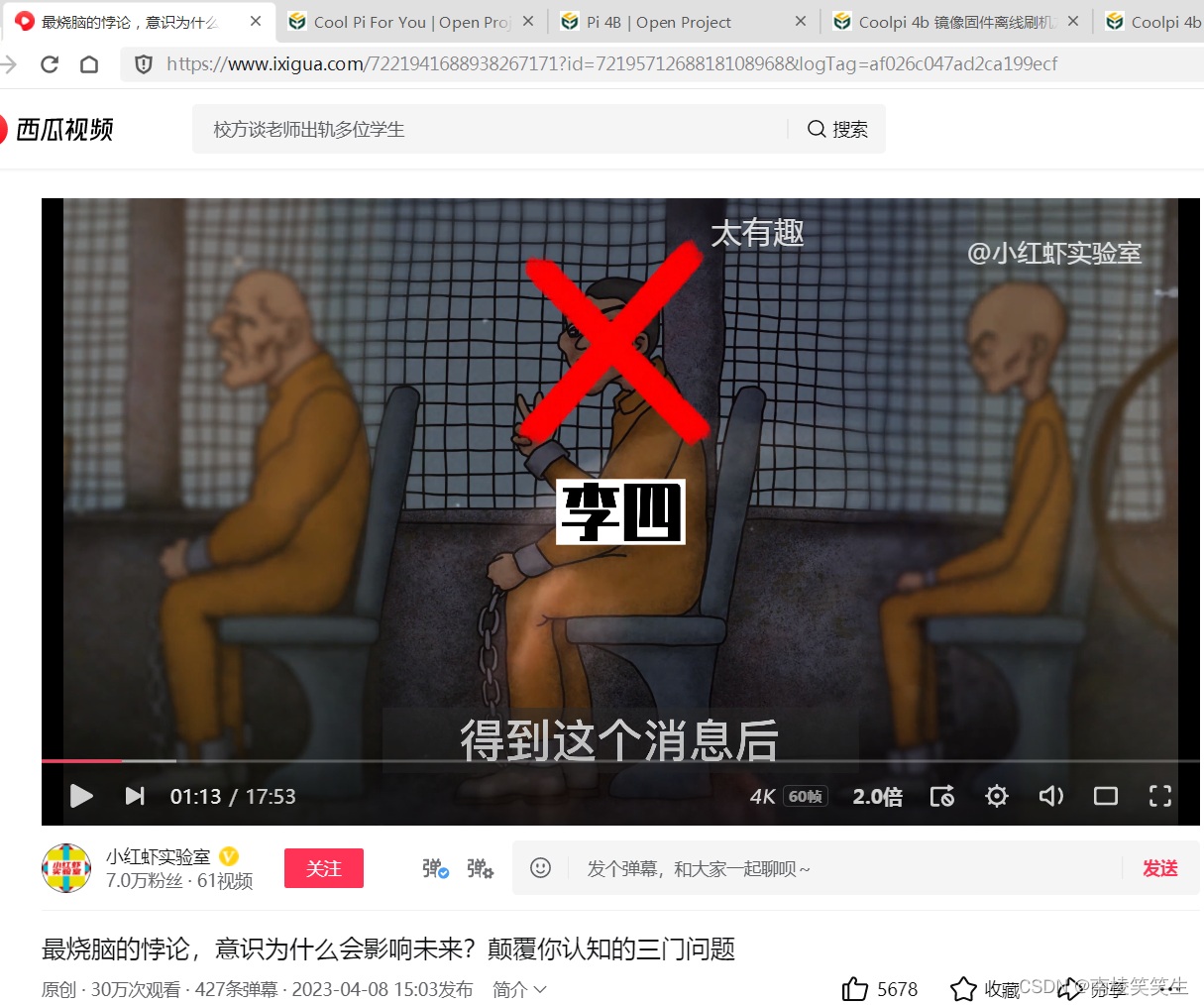
于是他启动逆向思维问看守:现在都知道3个囚犯当中有两个会被处死,只有一个人被释放。李四和王麻子这两个人中必有一人被处死,即便我知道这二人当中,谁会被处死,对我来说也并没有什么好处。那么,你能不能告诉我,谁还会被处死呢?”看守听后觉得很有道理,就告诉他,李四会被处死。得到这个消息后,张三兴奋不已。
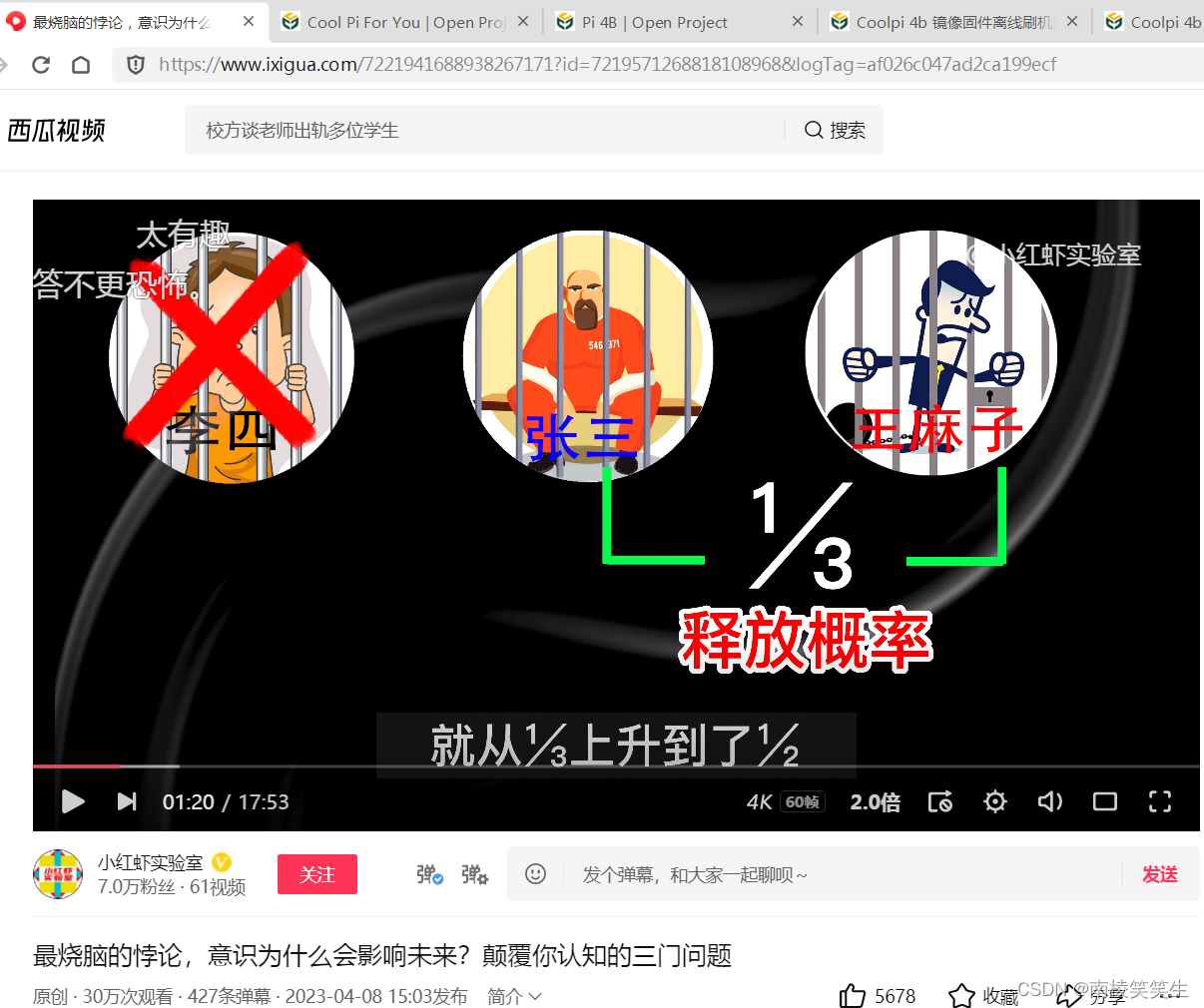
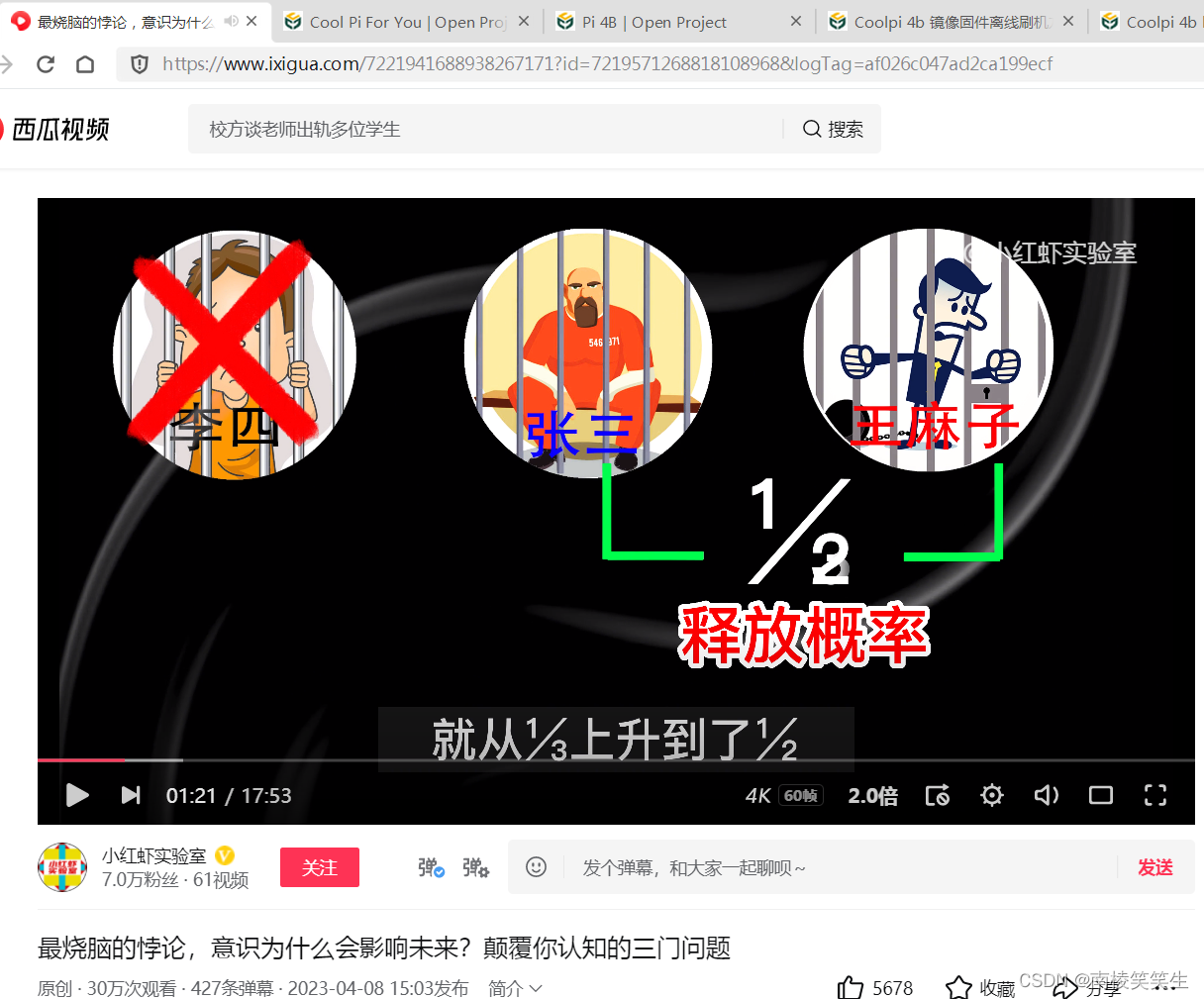
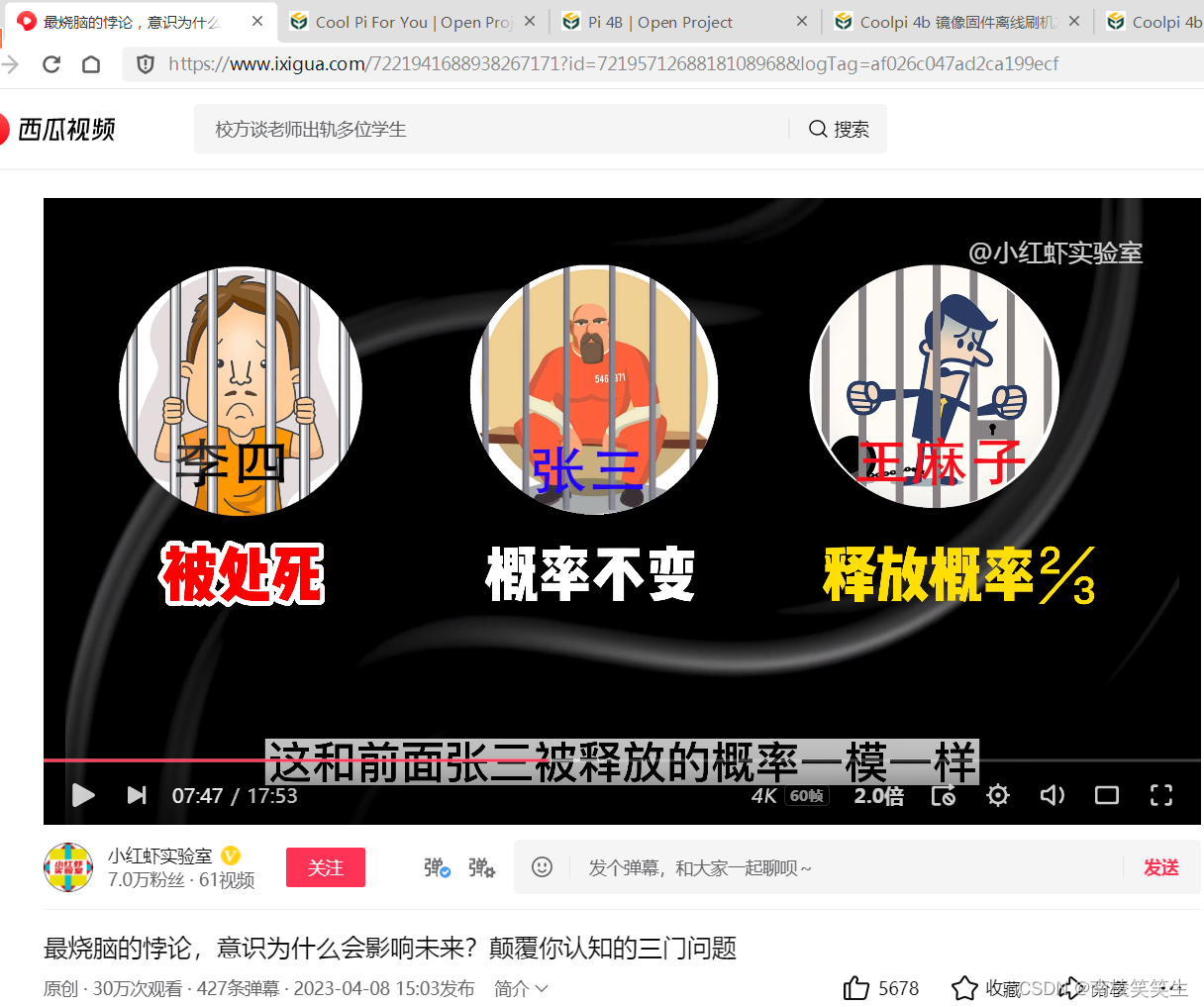
他认为李四被处死,自己和王麻子被释放的概率就从1/3上升到了1/2。按照张三的逻辑,他被处死的概率同样也会变为1/2。屏幕前的你,是不是和张三算出的概率一样呢?但是你知道吗这个结果是错误的。正确的答案是:李四被处死,张三被释放的概率不变,王麻子被释放的概率将提升至2/3。这是为什么呢?稍后我会专门讲到。现在我们还得从全世界智商最高人说起。
问玛丽莲
最烧脑的悖论,意识为什么会影响未来?颠覆你认知的三门问题
时间来到1946年8月,在美国密苏里州圣路易斯出生了一个美貌与智慧集于一身的女性——玛丽莲·沃斯·莎凡特。在她10岁的时候,初次接受斯坦福-比奈智商测验,测得智商高达228 。在之后的数十年间,她陆陆续续接受过数次的智力测试,最高达到了243.这个数值,放在今天都是第一。因此她也成为了吉尼斯世界纪录中,有史以来智商最高的人类,没有之一。
这也直接改变了玛丽莲的生活。开始频频出现电视和媒体上,包括航空杂志,成为了当时小有名气的人物。这么聪明的人一般会干什么呢?当然是把自己的聪明才智最大化的利用,玛丽莲是个罕见的天才,热衷于解答各种各样的难题。于是在1985年,玛丽莲就《周日杂志》上开设了一个专栏,叫做《问玛丽莲》。观众有什么不懂的事儿,都可以通过专栏问她。包括逻辑、数学、天文、脑筋急转弯等问题都可以,专栏办的很火爆也很成功。
然在在1990年的某一天,玛丽莲就收到了一封很奇怪的信,让她帮忙解决一个简单的数学问题。玛丽莲看过信之后,稍加思索之后,就写出了答案。并且发表在《问玛丽莲》的专栏上,玛丽莲的这顿操作,直接捅了马蜂窝。当时的专栏读者大概有1万人,其中拥有博士学位的读者就有1000人。
这些高学历的见到玛丽莲的答案后,纷纷给玛丽莲写信,参与讨论。一些人直接开喷,说它她就是个民科,根本不懂数学。甚至她的答案却引起了十几位数学家注意,开启了长达20多年的数学对战。也正是这次讨论,深刻的影响了统计学、概率学、人工智能、互联网和人机互联的发展。那么这位观众的信中究竟写了什么样的数学题呢?
做个交易吧
其实这个问题源自1970年,美国纽约电视台创办的一个电视游戏节目,叫做《让我们做个交易吧》。主持人在台上放置了三扇关闭了的门,其中一扇门的后面藏着一辆跑车,其余两扇门的后面藏的则是更为便宜的东西,比如说其它两扇门的后面藏的是羊。游戏的规则就是让参与者从这三扇关闭的门中做出选择,如果参与者选中了藏有跑车的门,那么他将会获得奖品就是这辆跑车,如果选择的门后面没有跑车而是羊,则挑战失败,没有任何奖品。对于每一个参与者来说,肯定是想选中藏着跑车的那扇门。
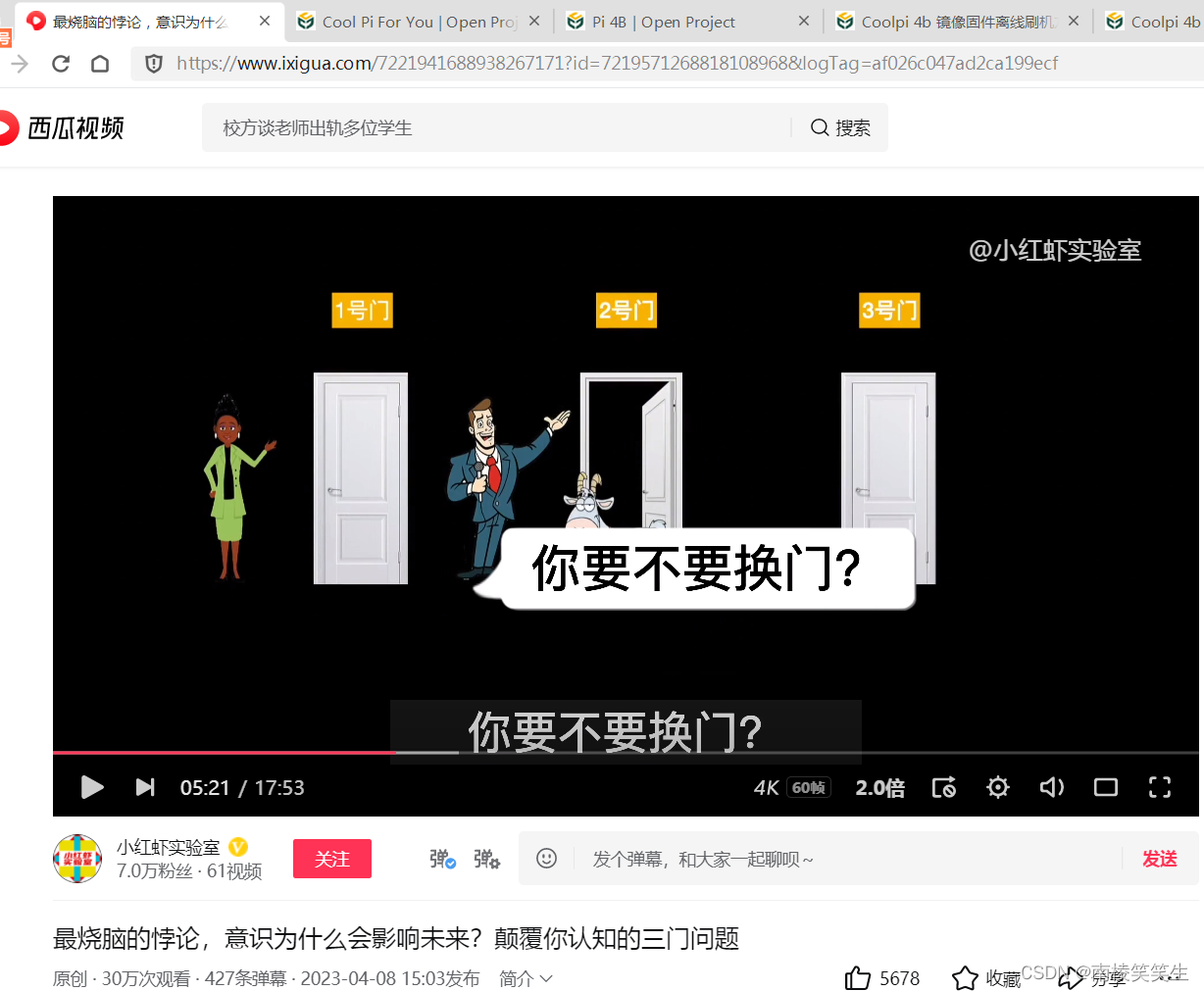
刚开始的时候,游戏规则还是比较简单的,就是嘉宾随意选一个门,主事人打开。要是抽中跑车,那就赚到了。大家看明白了吗?不论你选择开哪一扇门,中奖的概率都是1/3。几期节目之后,主持人认为这样的规则太过单调,缺乏舞台的活力。于是他在游戏环节中和参与者打心理战,经常突如其来地变换游戏规则,给参赛人和观众都来个猝不及防,既使得观众们困惑不已,又迫使参赛者“脑筋急转弯”。具体操作是这样的,在参与者选定一扇门之后,主持人并不急于的打开参与者选择的那扇门,宣布游戏的结果。而是选择打开另一扇藏着山羊的门。这里需要说明的是,主持人是知道跑车在哪扇门后面的。然后问参与者是否换门。
比如当一位参与者选中了1号门之后,主持人则打开了2号门,2号门后门则是一只羊。这个时候主持人就会问参与者,你要不要换门?我想大部分人的第一反应,和参与者是一样的,换门和不换门有什么区别吗?一共就只有三扇门,打开了一扇藏着羊的门。剩下的两扇门中,必定有一扇能够中奖,一扇不能。换不换的概率不都是1/2吗?这个时候你会作何选择呢?大部分的观众都支持不换门,参与者也认为换门没有意义,于是就没有换门。结果1号门的后面是一只羊。
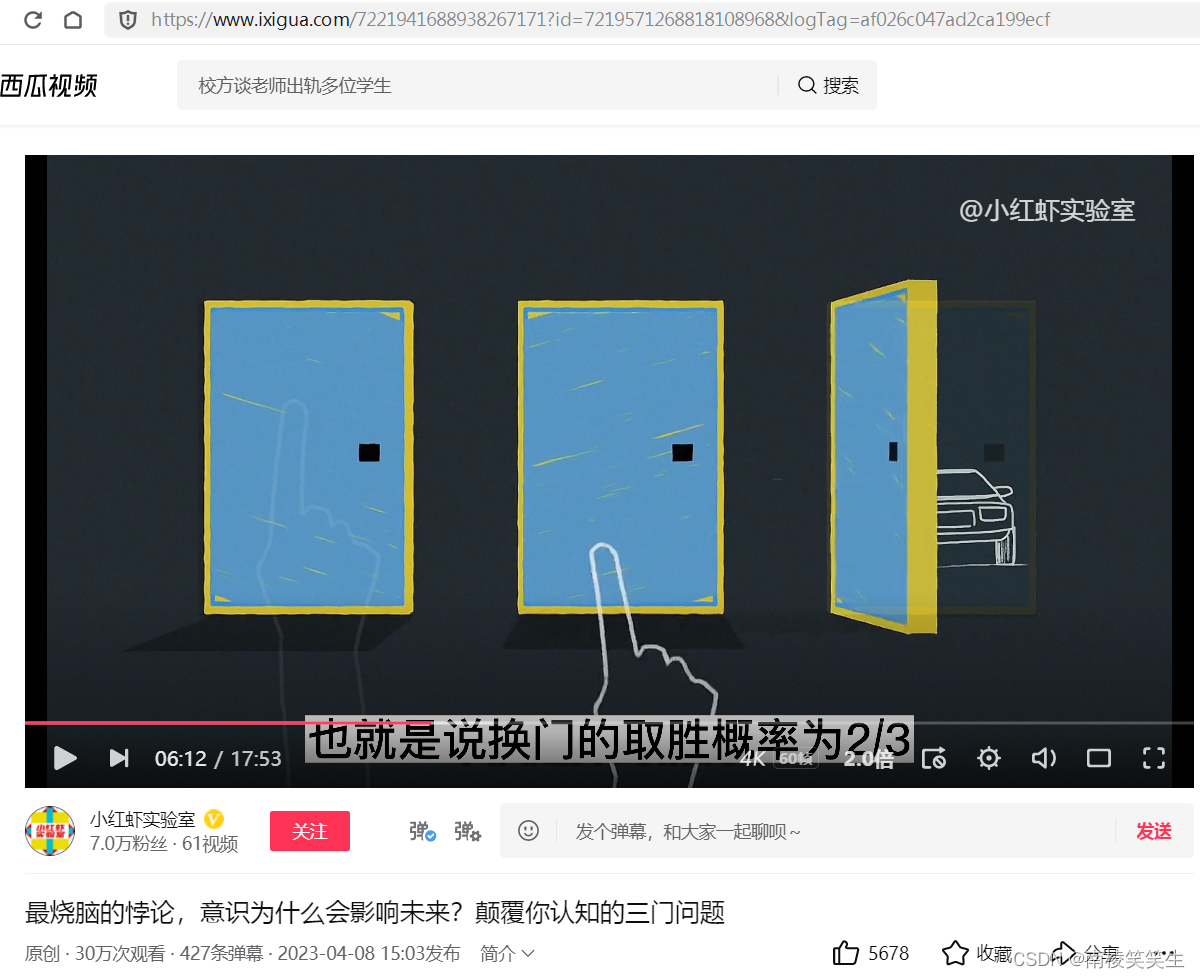
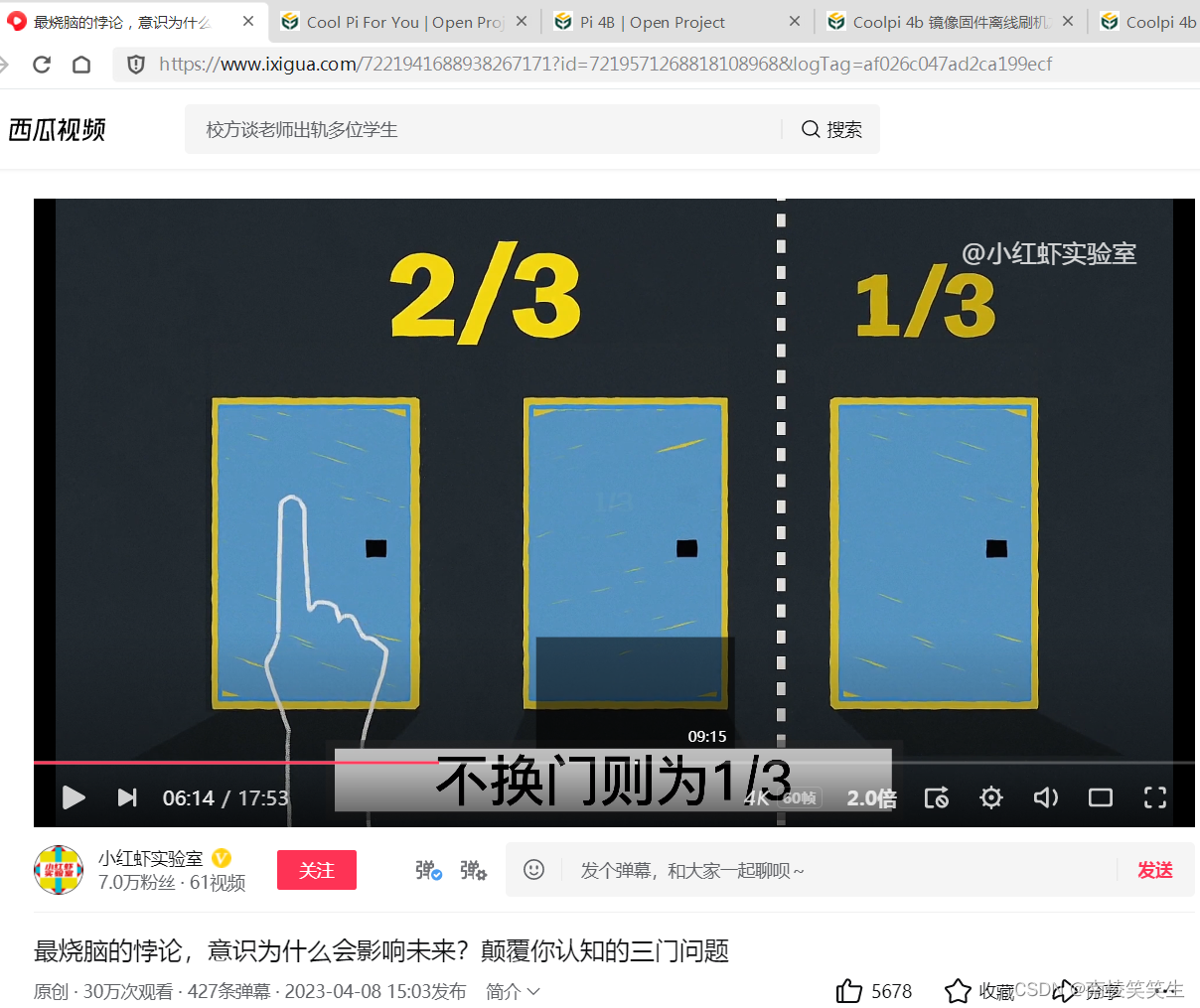
这个节目非常的火爆,但是参与者却没有严肃的思考过是否应该选择换门这个问题 。这个时候有人就想到了智商最高的人玛丽莲·沃斯·莎凡特。并写信问她,你帮忙给推算推算,从科学的角度,到底该不该换门呢?经过一番思索之后,玛丽莲回复的是“应该换门”。玛丽莲认为换门后获胜的概率是不换门的两倍。也就是说换门的取胜概率为2/3,不换门则为1/3。
玛丽莲的回复如同捅了马蜂窝一样,引起了轩然大波。就出现了我们前面提到的,很多的读者给玛丽莲写信,批评她的回复是错误的。其中还有声称自己是已获得数学或统计学博士学位的专家学者,更是直言不讳的说:美国已经足够多的数学文盲了,我们不需要世界上智商最高的人,传播伪科学,这是对数学的侮辱。这么多人都反对玛丽莲,她真的错了吗?我们先来看看她是怎么解题的。
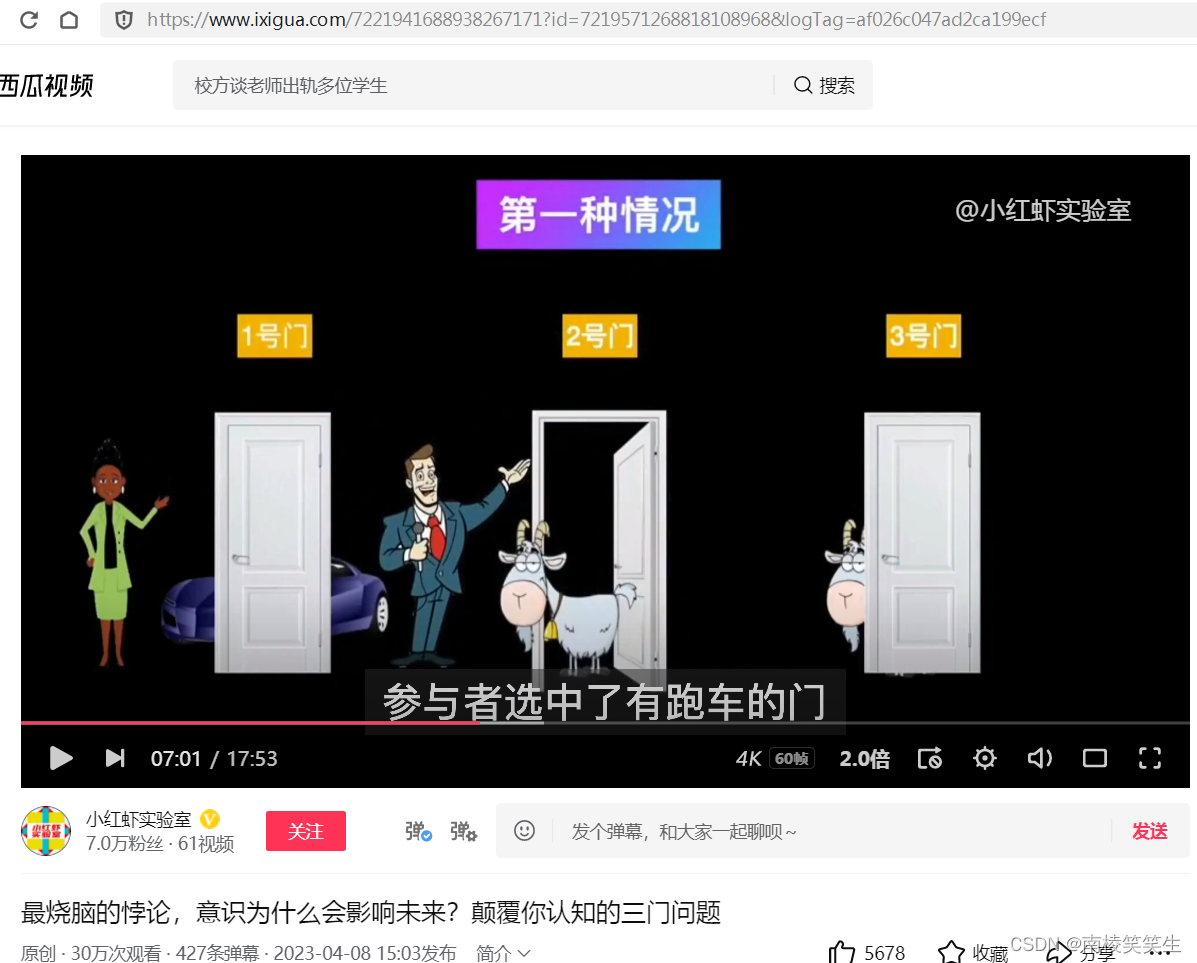
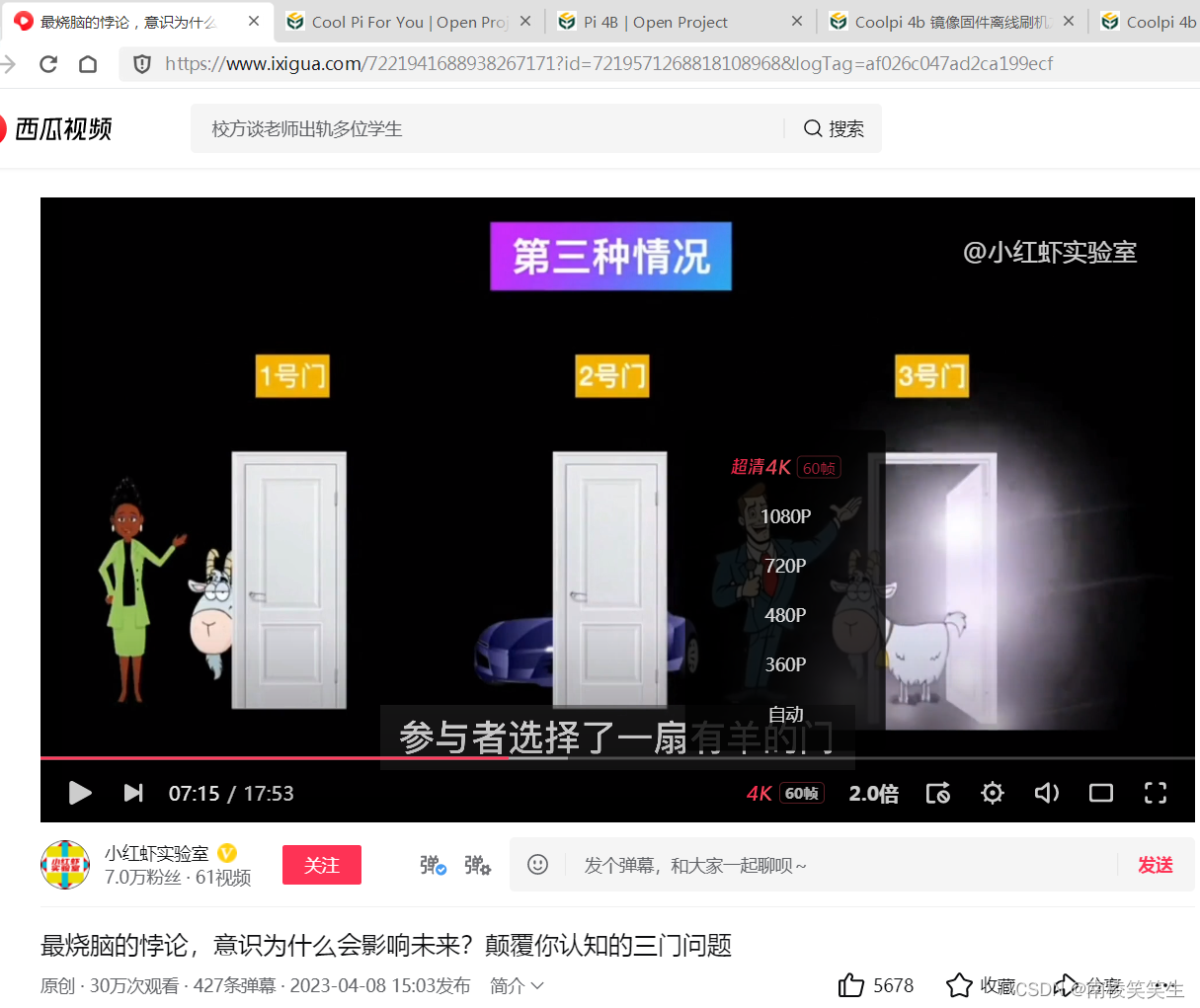
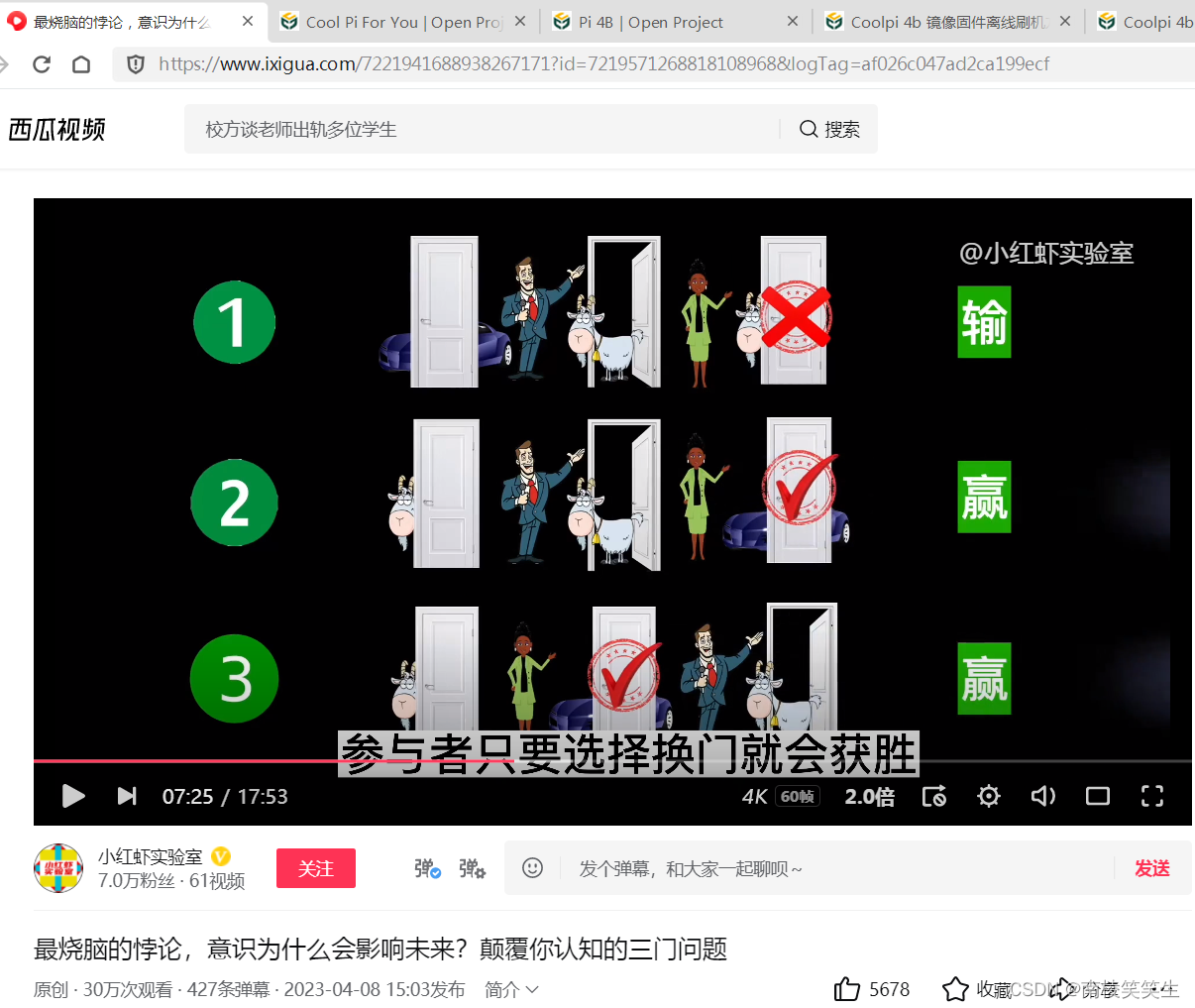
在玛丽莲收到读者的信后,就根据游戏画了一张图,她认为这个游戏只能出现以下的三种情况。参与者选择了一扇门,主持人打开了藏有羊的门,如果参与者换门出现的第一种情况,参与者选中了有跑车的门,换到了有羊的门;
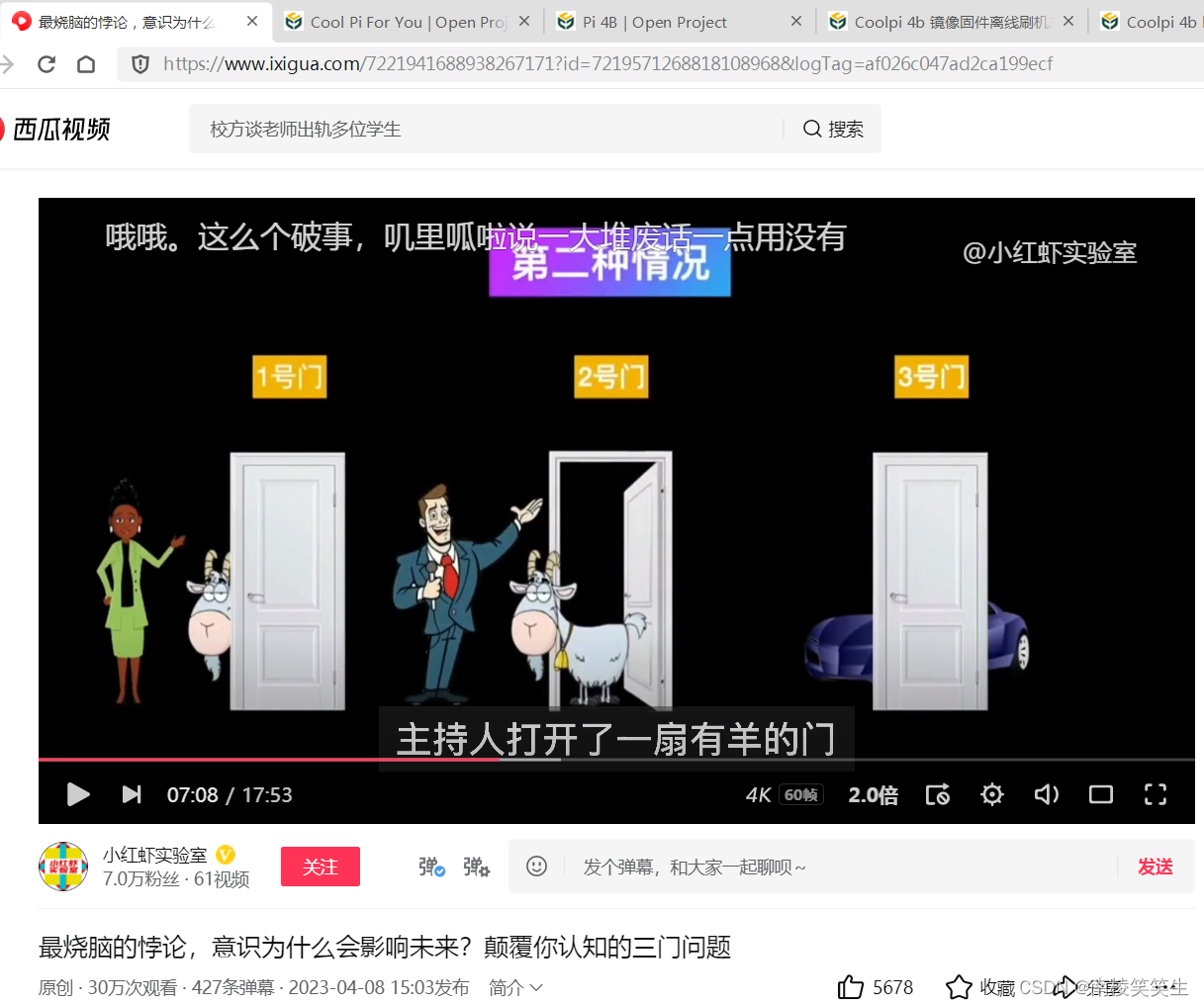
第二种嘉宾选择了一扇有羊的门,主持人打开了一扇有羊的门,如果这个时候换门,刚好获得跑车。
第三种情况和第二种情况差不多,参与者选择了一扇有羊的门,主持人打开了有羊的门,那只要参与者选择换门,就会获得跑车。
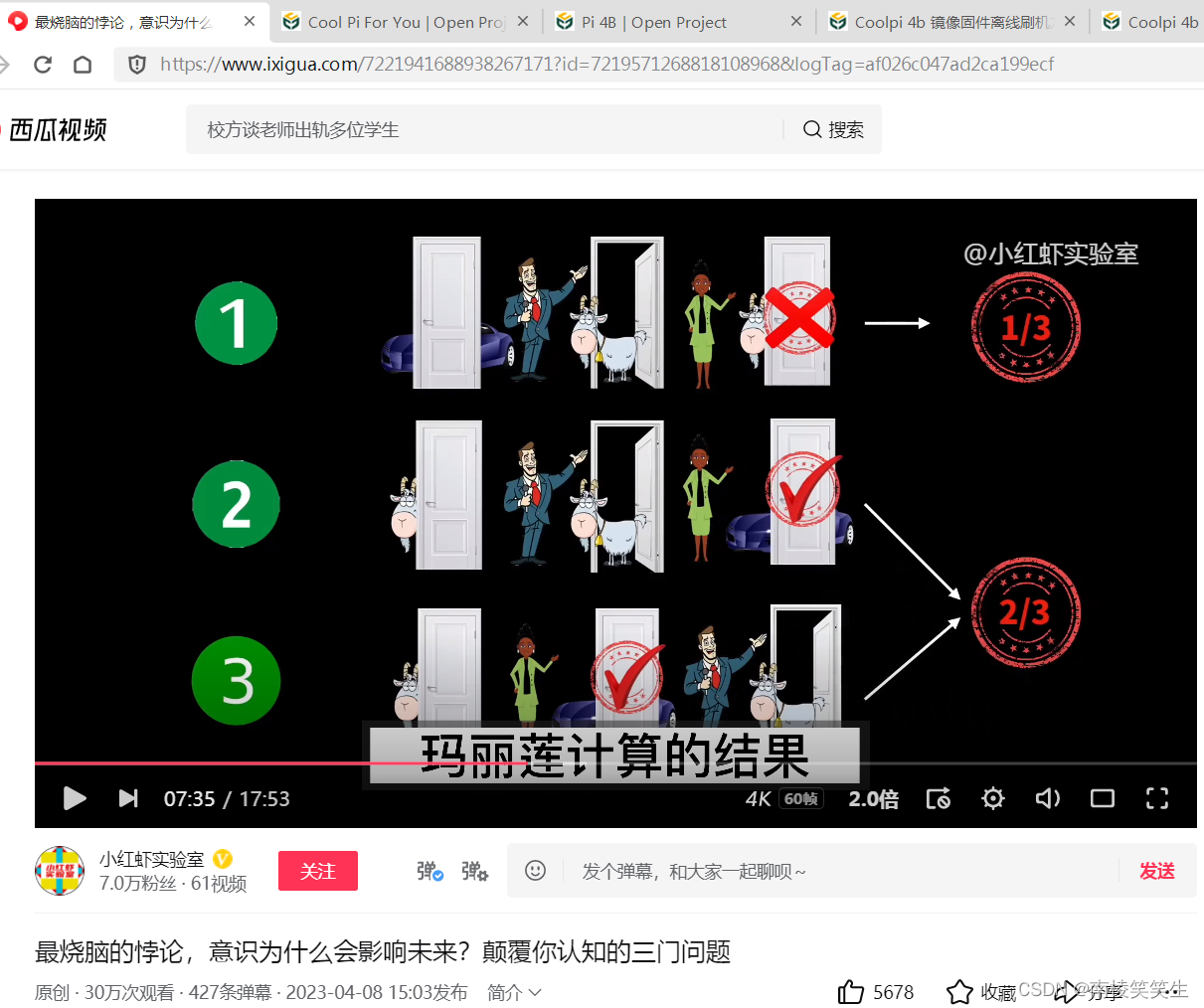
在第二种或第三种的情况里,参与者只要选择换门,就会获胜。所以玛丽莲得出的答案就是,只要参与者选择换门,获胜的概率就会提升到2/3。
玛丽莲计算的结果,和我们的直觉似乎背道而驰,直觉告诉我们换门与不换门中奖的概率都是1/2,玛丽莲的答案却是2/3。这和前面张三被释放的概率一模一样。
有点和英国著名物理学家托马斯·杨的双缝干涉实验很相似,有人观察的时候,光就会呈现了粒子状,屏幕上就会留下两条笔直光斑;没有人观察的时候,光就呈波状,终屏幕上会出现一道道的斑马线。难道主持人在开门的一瞬间,概率就自动转移到未被选中和打开的那一扇门上了吗?是不是感觉有点玄学的味道了,但是直觉告诉你,这是不可能的?难道是玛丽莲算错了吗?
验证真理
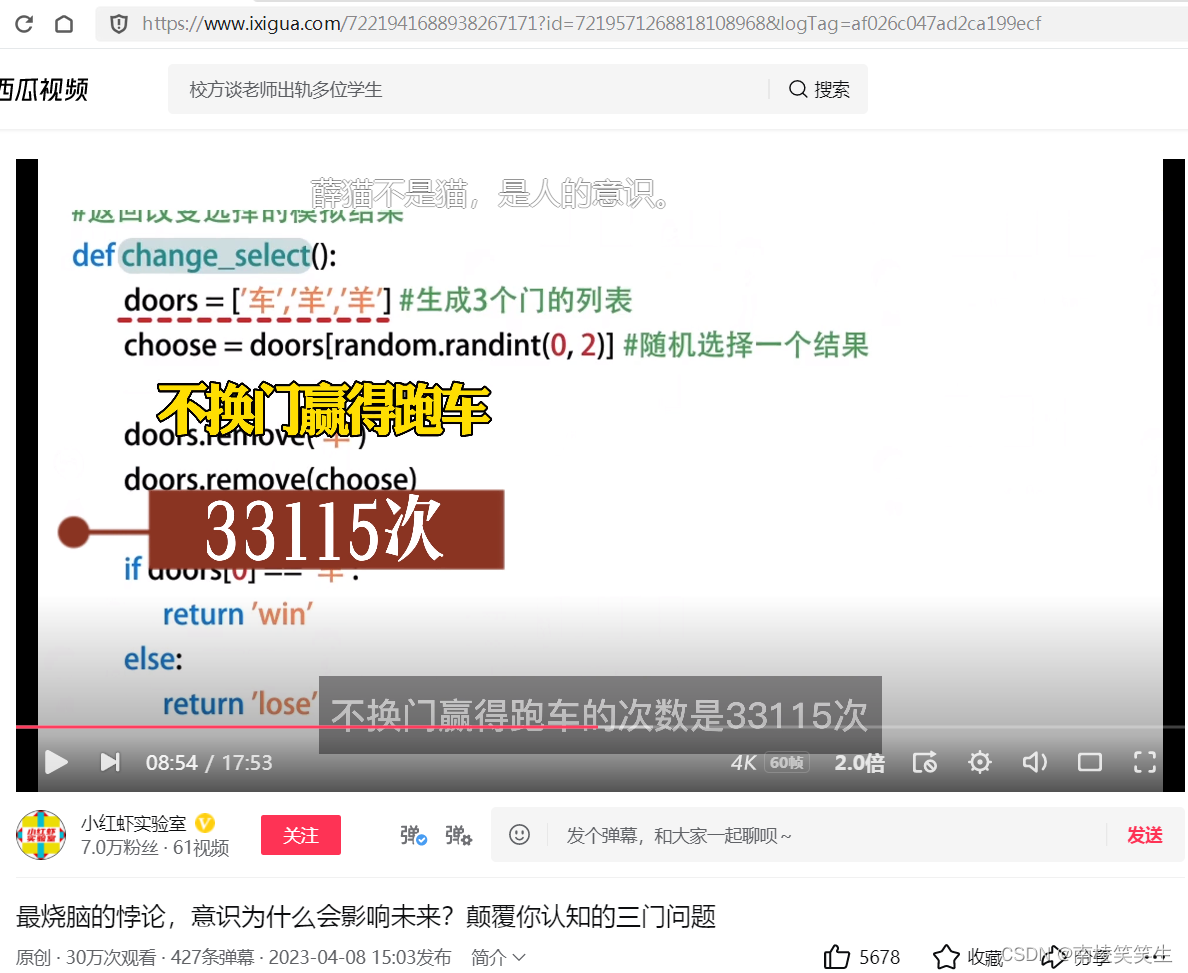
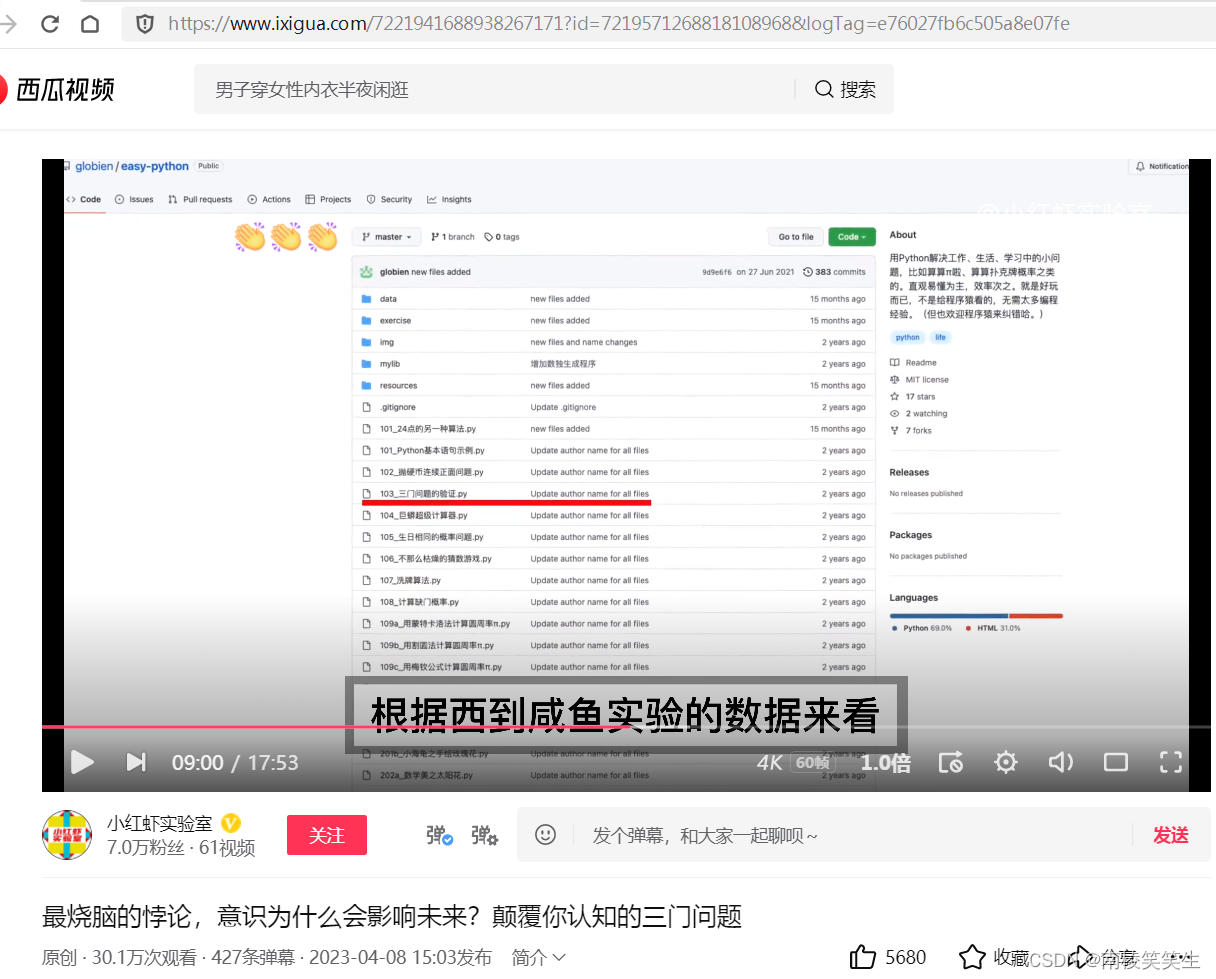
1978年5月11日,《光明日报》发表本报特约评论员文章《实践是检验真理的唯一标准》,这句话放在任何国家或任何领域,永远都不会过时。网上有一个网名叫做西到咸鱼的计算机大神,他认为检验玛丽莲计算的结果是否正确的唯一办法,就是通过计算机对游戏进行反复的演算。于是他单独编写了一套程序,取名为《三门问题的验证》。
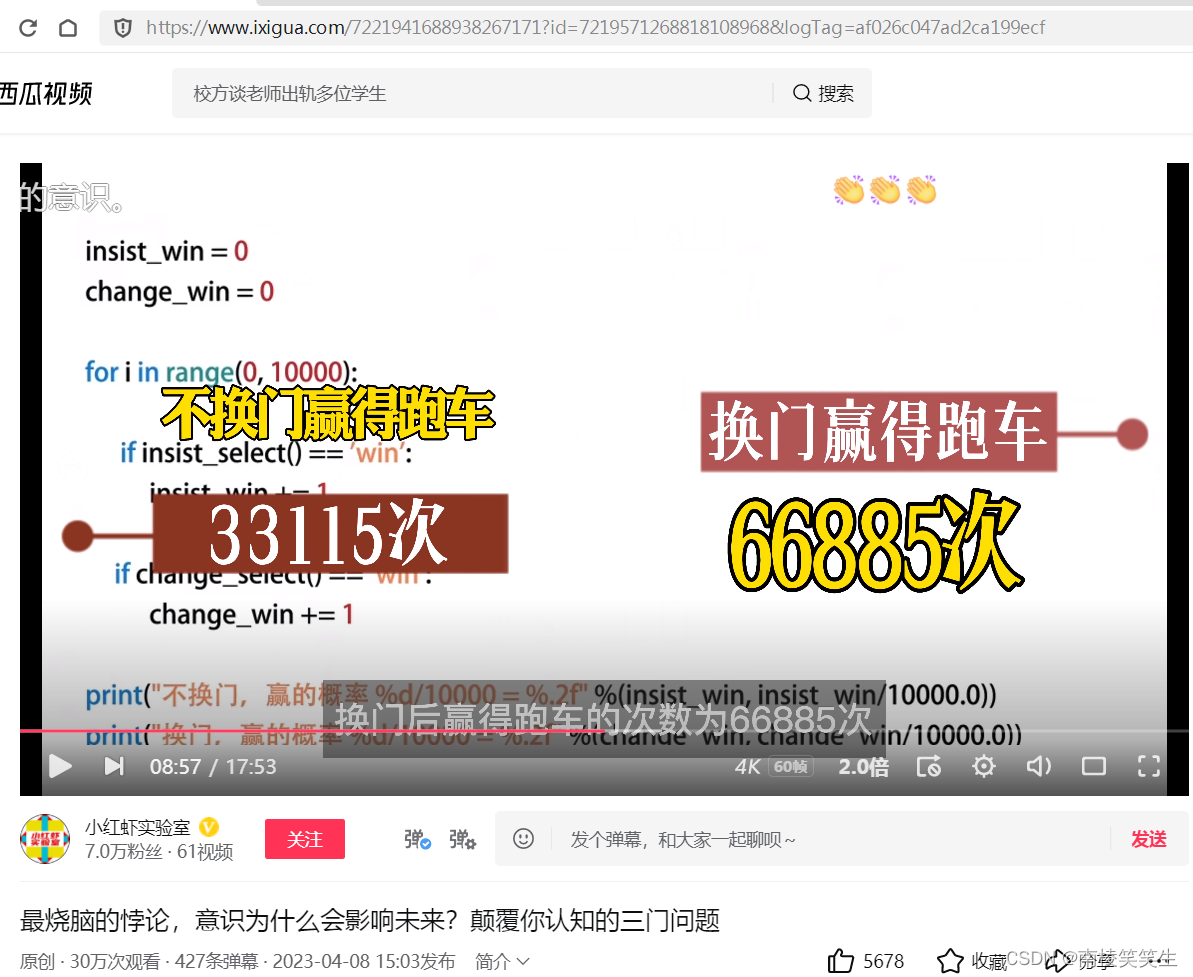
他用这个程序进行了10万次的推演,不换门赢得跑车的次数是33115次,换门后赢得跑车的次数为66885次。根据西到咸鱼实验的数据来看,换门后获奖的概率和玛丽莲计算出的概率很相似,提升到2/3。看来玛丽莲没有算错。
那为什么会产生和我们直觉不一样的结果来呢?为了更直观的弄清楚原因。于是就诞生了一个数学求婚的故事。话说哆啦A梦的好朋友大雄,交了一个女朋友,两人正在谈婚论嫁,大雄想让哆啦A梦送一枚钻戒给自己,作为求婚的戒指。
哆啦A梦不想大雄不劳而获,于是他就准备了6个戒指盒,把戒指任意放进其中的一个戒指盒。然后让大雄在从六个盒子中选出装有戒指的盒子,大雄觉得这个难度太大,根本没有把握完成,于是哆啦A梦改变了游戏的规则,他先让大雄指定一个盒子,先不打开。随后哆啦A梦从剩余的5个盒子中,打开四个空盒。然后问大雄要不要换盒子?
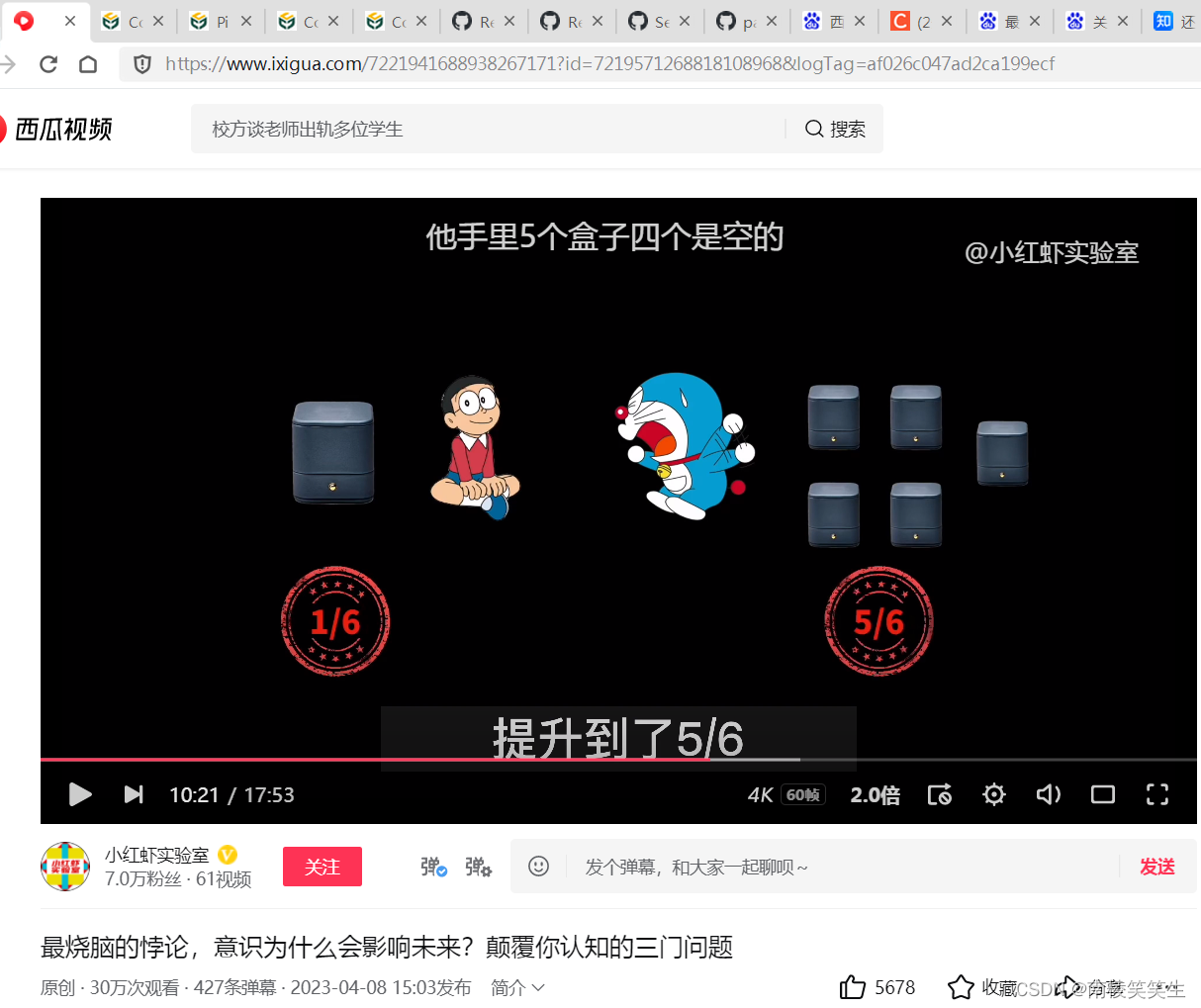
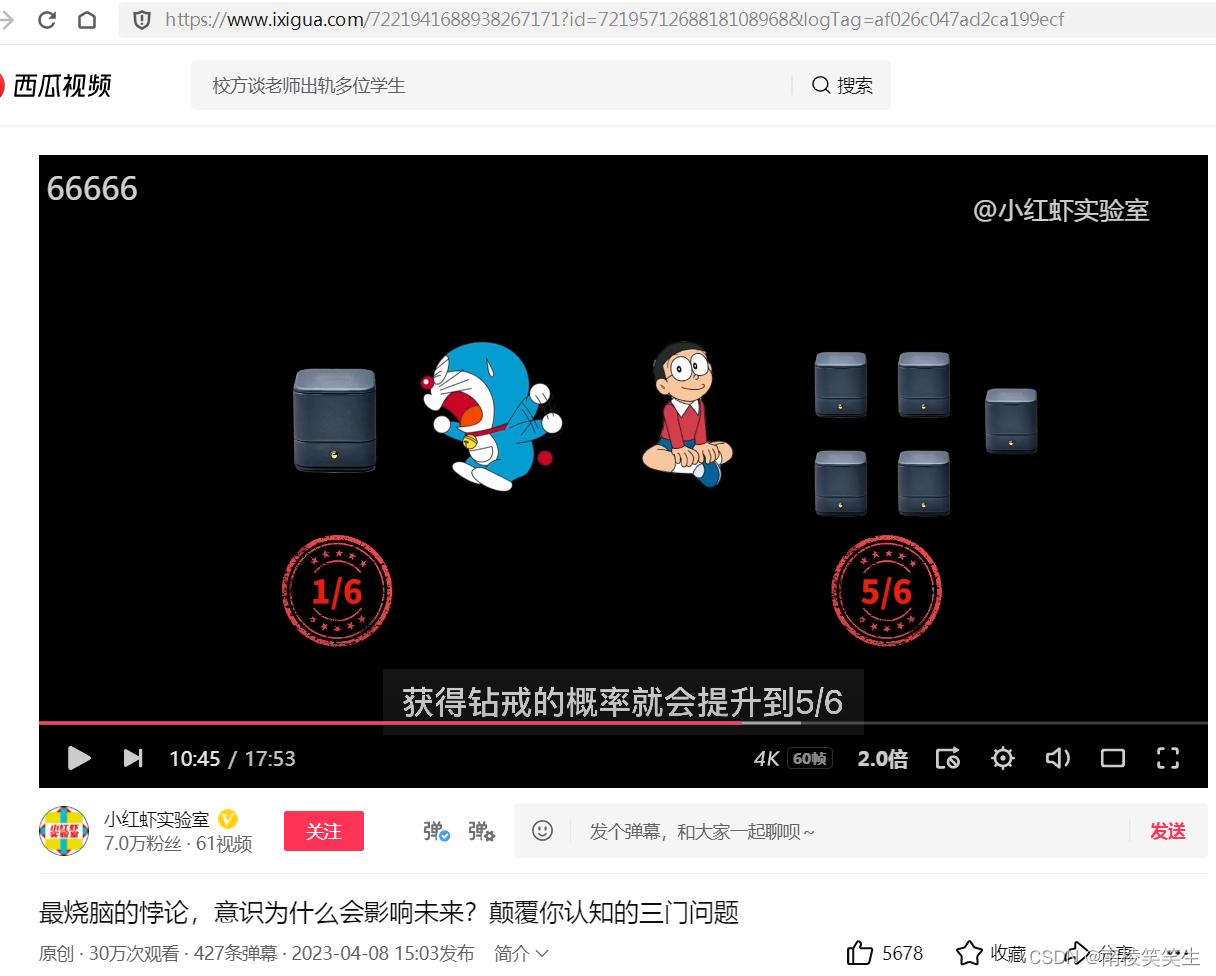
大雄瞬间就迷茫了,因为在他看来,生下两个盒子存在戒指的概率都是一样的,换不换盒子获得戒指的概率都是1/2。这回轮到哆啦A梦着急了,于是再一次的改变了规则,他问大雄愿不愿意用指定的盒子换他手里的5个盒子,这回大雄立马就同意了。大雄觉得一个换5个,获得戒指的概率一下子就从1/6提升到了5/6.就在交换之前,哆啦A梦,发出了灵魂一问:这两种选择有什么区别吗?
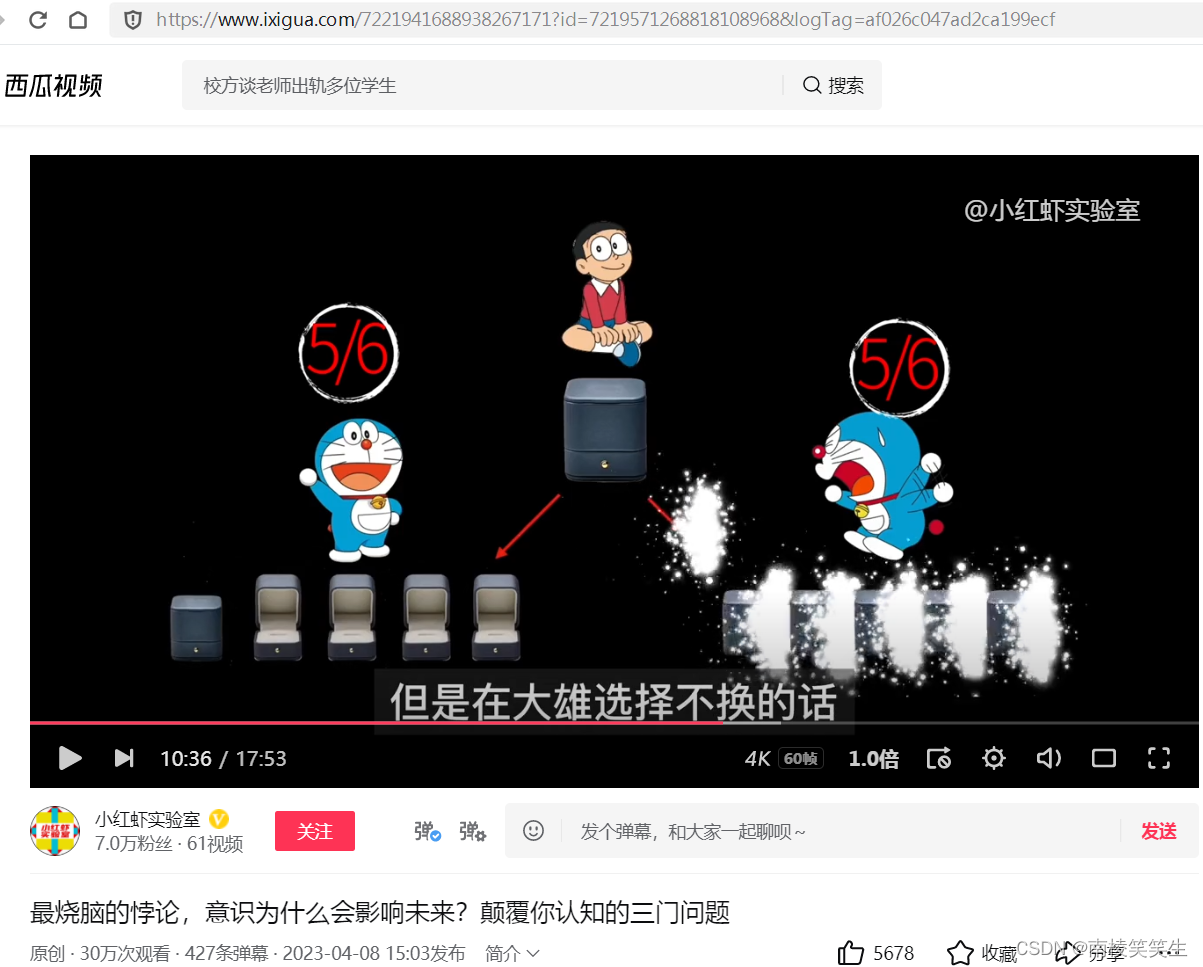
其实这两种选择没有任何的区别,实际上都是用一个盒子换5个盒子,获得钻戒的概率都是5/6.但是在大雄选择不换的话,获得钻戒的概率就只有1/6。大家发现没有,不论哆啦A梦打不打开盒子,只要大雄交换,获得钻戒的概率就会提升到5/6。那为什么我们会和大雄一样,在第一次的选择中,面对哆啦A梦打开的4个盒子,会认为剩下两个盒子中装有戒指的概率都是1/2呢?要想弄清楚这个问题,必须要把200多年前的一个牛掰的数学给请出来。
贝叶斯定理
时间回到1763年,清乾隆二十八年。英国神学家、数学家、数理统计学家和哲学家,概率论理论创始人,托马斯·贝叶斯去世了。他的朋友在帮他整理遗物的时候,发现了贝叶斯撰写的尚未出版的一本概率学书稿。贝叶斯的朋友整理好这些书稿后,取名为《论机会学说中一个问题的解》,并于次年出版。
不过这本书在出版后的一百多年的时间,都没有引起人们的注意。直到第二次世界大战期间,英国著名的数学家和逻辑学家阿兰·麦席森·图灵发展了贝叶斯理论。破解了德国的海军密码。人们才发现,贝叶斯竟然如此的伟大,绝对是数学家的一代宗师。从此拉开了贝叶斯理论大行其道的序幕。
科学家将贝叶斯理论称之为贝叶斯定理或贝叶斯推理,贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。说的直白些,人们根据不确定性信息作出推理和决策需要对各种结论的概率作出估计,这类推理称为概率推理。概率推理既是概率学和逻辑学的研究对象,也是心理学的研究对象,但研究的角度是不同的。

这样说可能会很死板,我们换个方式,你就很容易理解了。某天你见到了赌神老周,老周有想和你玩一玩,可是你是个十全好青年,从来没玩过牌,也根本不会。怎么办呢?老周就想了个办法,那就是抛硬币,以正反面论输赢。赌神和你抛硬币,你用什么方法赢赌神呢?
机智的灵光一现,想出来一个十佳的好办法。那就是把抛硬币的次数延长至一万次。这样一来,不论赌神是选择正面还是反面,在一万次的抛硬币中,每一面出现的概率都会非常接近50%。也就是说你有很大的机会和赌神老周打一个平手。一句话概括就是用因推算出果,这就是概率推理。
但是这场博弈你和赌神关注的方向,不在一个奇点上。你关注的是如何和赌神打成平手,赌神则更在意博弈的公平性。在赌神看来,你明知他是赌神,却竟敢一较高下。他担心你会出老千,比如用两面一样的假硬币比赛。赌神如何破解呢?
贝叶斯公式
当然不能和电影里一样,来一场枪战了。他打算用贝叶斯公式,来进行逆概率的推理。P(A|B)=P(B|A)*P(A)/P(B)。这个公式看着复杂,其实非常简单,基本上都能推算。其中P代表概率所对应的事件,比如P(A) 是 A 发生的概率;P(B) 是 B 发生的概率;P(A|B) 是在 B 发生的情况下 A 发生的概率;P(B|A) 是在 A 发生的情况下 B 发生的概率。公式用汉语表述则是后验概率 = (似然度 * 先验概率)/标准化常量 。也就是说,后验概率与先验概率和似然度的乘积成正比。
我们举一个例子就会很好的理解。比如一间房屋在过去一年内共被盗窃过3次,在房屋内养了一条狗,这条狗每天晚上会叫一次。我们假设盗贼在接近或潜入房屋时,狗叫的概率为0.9.那么当狗叫时,发生入室盗窃的概率是多少呢?
根据公式,我们可以把狗每天叫的事件概率定义为1,也就是P(A),盗贼入侵事件的概率为3/365。P(B)则约等于0.008;盗贼入侵时的狗叫概率P(A|B)为 0.9;求狗叫时盗贼入侵的的概率也就是P(B|A)应该是多少?根据贝叶斯公式,即可求得:P(B|A) = 0.9 * 0.008 / 1 = 0.0072。你学会了吗?
那么赌神计算出来的这枚硬币做手脚的数值是多少呢?第一次硬币正面朝上,赌神带入公式,最后得出的数值为0.82.也就是说硬币两面都是正面的概率则是1-0.82=0.18也就是这枚硬币做手脚的概率为18%。

第二次抛硬币还是正面朝上,那这枚硬币被做手脚的概率就上升到了31%,第三次正面朝上,那么做手脚的概率则是47%。第四次还是正面朝上,做手脚的概率就上升到了74%。跑四次硬币,四次都是正面朝上,从贝叶斯公式中,我们可以看出,这枚硬币被做手脚的概率非常大。所以赌神正确的选择是叫停比赛,检查硬币。检查完毕后,证明硬币没有问题,于是他根据贝叶斯公式后验概率,计算出他们将在1万次的抛硬币后打成平手。
我们再回到大雄的选择题当中,在常规的概率中,不论大雄换不换盒子,都不能改变戒指就在某个盒子里的事实。也就是说没有人能够通过换盒子改变戒指的时空位置。所以我们认为钻戒在两个盒子的概率都是1/2。这就有点说不通了,为什么三囚犯中的张麻子和三门问题换门后的概率都提升到了2/3呢?
最后的真相
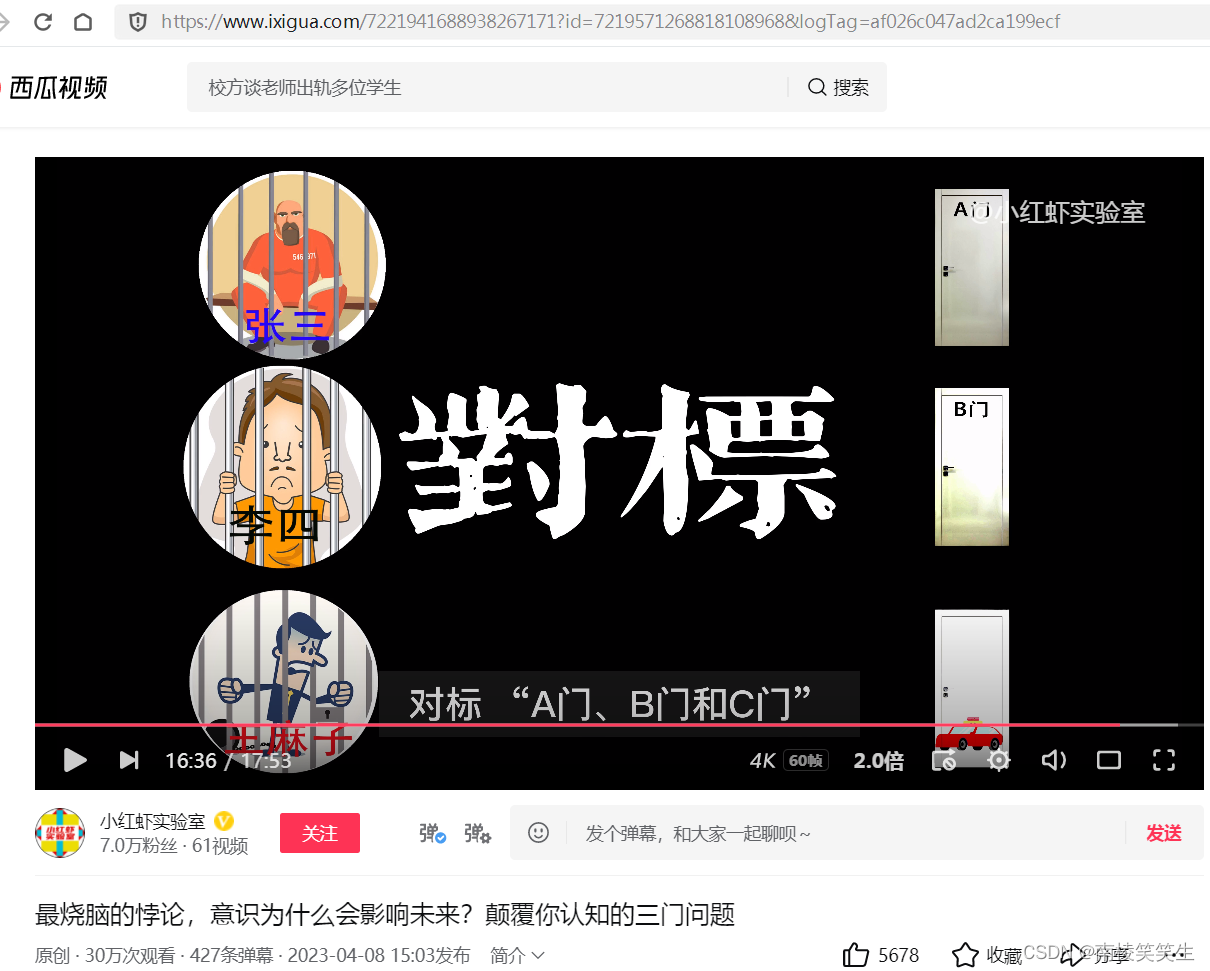
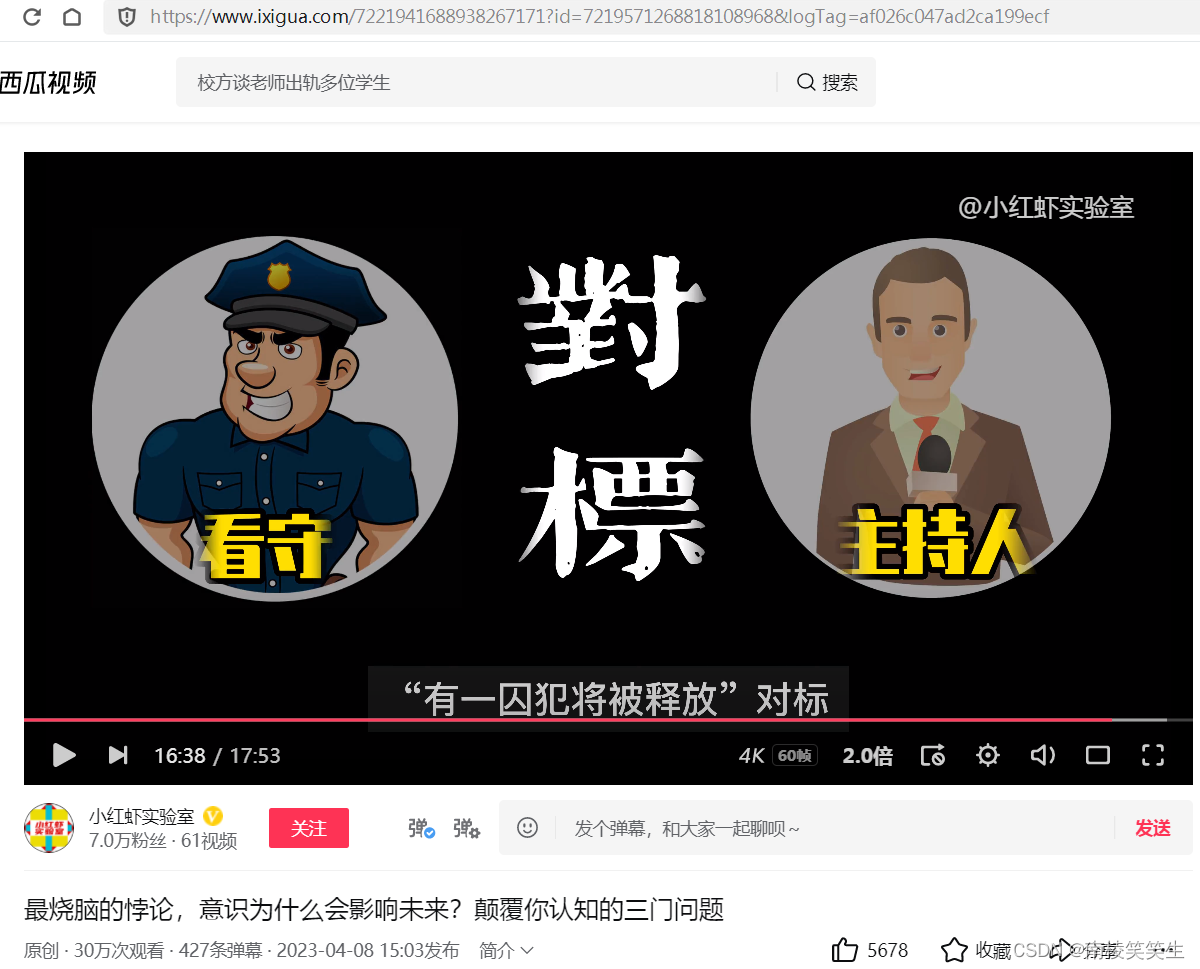
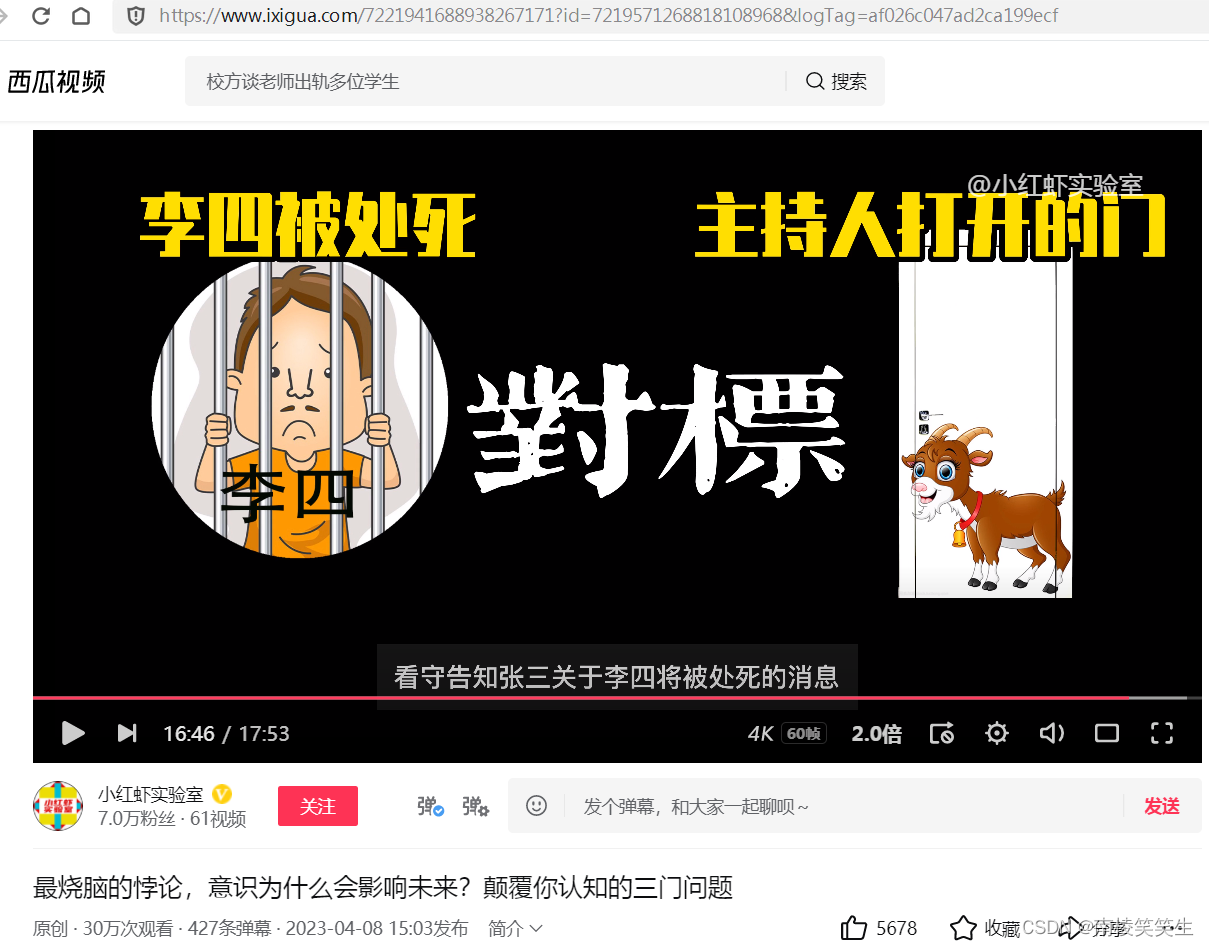
这里我们需要重新的做一个梳理,“张三、李四和王麻子”对标 “A门、B门和C门”;“主持人”对标“监狱看守”;“有一囚犯将被释放”对标“有一个门后有轿车”;看守告知张三关于李四将被处死的消息”VS“打开B发现门后没有轿车”。通过对比可以看出,“三囚犯问题”和“三门问题”具有相同的结构,本质上完全相同,都是典型的贝叶斯概率问题。



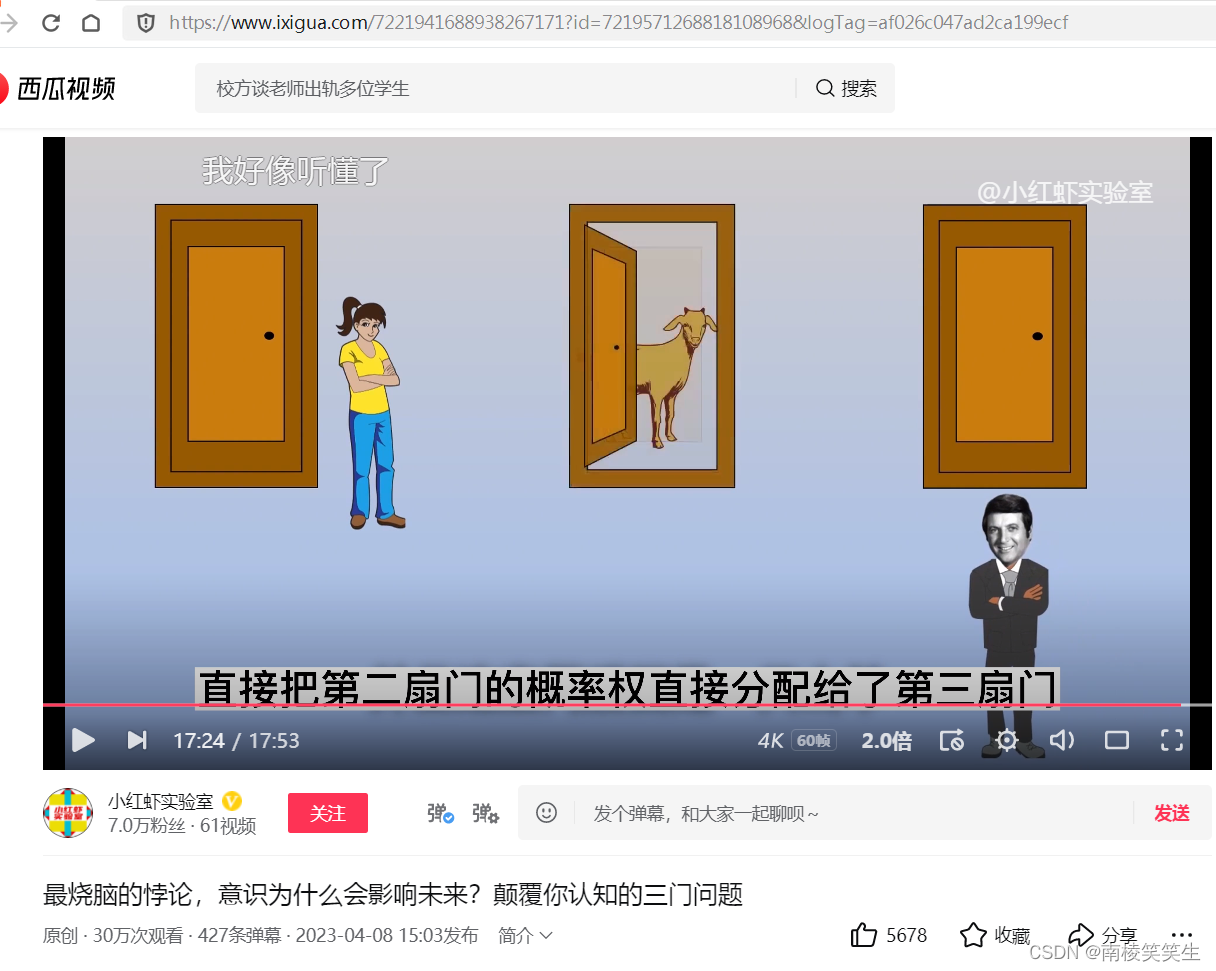
在三门问题中,主持人和参与者所获得的信息是不对称的,因为主持人是知道哪扇门的后面藏着跑车的。参与者和观众对此一无所知,所以大多数认为换不换门中奖的概率都是1/2。但是在参与者选中的门被打开之前,主持人主动为参与者排除了一个错误选项。也就是主持人的这个操作,直接把第二扇门的概率权直接分配给了第三扇门,所以不换门,获奖的概率依然是1/3,换门后获奖的概率就是2/3。你看,对于不懂概率的人,他中大奖的概率只有1/3;对于懂概率的人来说,他中大奖的概率将成倍增加,甚至获奖率能够达到100%。
20230516使用python3确认三门问题
2023/5/16 18:38
今天将这个视频重看了3次【以前就看过一次】,今天终于把【三门问题】搞明白了!
https://www.ixigua.com/7221941688938267171?id=7219571268818108968
最烧脑的悖论,意识为什么会影响未来?颠覆你认知的三门问题
原创 · 30.1万次观看 · 427条弹幕 · 2023-04-08 15:03发布
在https://github.com/
搜索:globien/easy-python
https://github.com/globien/easy-python

百度搜索:103 三门问题的验证.py
103_三门问题的验证.py
# 作者:西岛闲鱼
# https://github.com/globien/easy-python
# https://gitee.com/globien/easy-python
# 验证三门问题(Monty Hall problem)
import random
获奖次数_不换 = 0 # 不换而获奖的计数器
获奖次数_换 = 0 # 换而获奖的计数器
试验次数 = 100000 # 换和不换各做这么多次实验
for i in range(试验次数): # 不换的实验
door_list = ["A","B","C"] # 三扇门的编号
car = random.choice(door_list) # 汽车随机放在某扇门后
bet = random.choice(door_list) # 挑战者随机选择一扇门
if bet == car: # 不换!直接揭晓答案
获奖次数_不换 = 获奖次数_不换 + 1
for i in range(试验次数): # 换的实验
door_list = ["A","B","C"] # 三扇门的编号
car = random.choice(door_list) # 汽车随机放在某扇门后
bet = random.choice(door_list) # 挑战者随机选择一扇门
# 现在主持人随机选择一扇门予以排除
# 这扇门不是挑战者选择的门,也不是汽车所在的门
host_list = ["A","B","C"]
host_list.remove(bet)
if car in host_list:
host_list.remove(car)
discard = random.choice(host_list)
# 现在挑战者决定换,即换成剩下的一扇门,看看是否获奖
door_list.remove(bet) # 去掉自己已经选过的门
door_list.remove(discard) # 去掉主持人排除的门
bet = door_list[0] # 只剩下一扇门,换成它!
if bet == car: # 换!揭晓答案
获奖次数_换 = 获奖次数_换 + 1
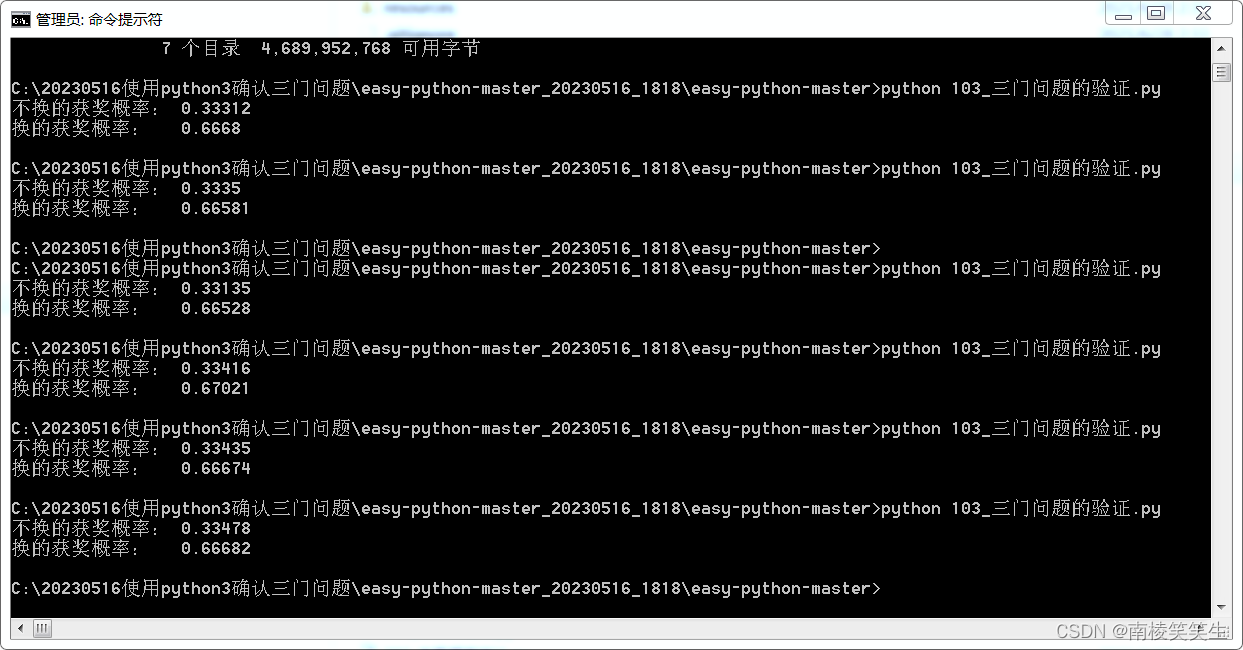
print("不换的获奖概率:", 获奖次数_不换/试验次数)
print("换的获奖概率: ", 获奖次数_换/试验次数)
调试记录:
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>python 103_三门问题的验证.py
不换的获奖概率: 0.33312
换的获奖概率: 0.6668
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>python 103_三门问题的验证.py
不换的获奖概率: 0.3335
换的获奖概率: 0.66581
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>python 103_三门问题的验证.py
不换的获奖概率: 0.33135
换的获奖概率: 0.66528
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>python 103_三门问题的验证.py
不换的获奖概率: 0.33416
换的获奖概率: 0.67021
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>python 103_三门问题的验证.py
不换的获奖概率: 0.33435
换的获奖概率: 0.66674
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>python 103_三门问题的验证.py
不换的获奖概率: 0.33478
换的获奖概率: 0.66682
C:\20230516使用python3确认三门问题\easy-python-master_20230516_1818\easy-python-master>
视频的代码【怎么和github的代码差异太大了,以我的经验是两种风格!】
# coding=gbk
#from random import choice
import random
#返回坚持选择的模拟结果
def insist_select():
doors = ['车', '羊', '羊']
choose = doors[random.randint(0,2)]
if choose == '车':
return 'win'
else:
return 'lose'
#返回改变选择的模拟结果
def change_select():
doors = ['车', '羊', '羊'] #生成3个门的列表
choose = doors[random.randint(0,2)] #随机选择一个结果
doors.remove('羊') #从doors中去掉一个羊的门
doors.remove(choose) #再去掉我们开始
#if choose == '车':
#if doors[0] == '羊':
if doors[0] == '车':
return 'win'
else:
return 'lose'
insist_win = 0 #记录不换门胜利的次数
change_win = 0
#for i in range(0, 1000):
for i in range(0, 10000):
if insist_select() == 'win':
insist_win += 1
if change_select() == 'win':
change_win += 1
print("不换门,赢的概率 %d/10000 = %.2f"%(insist_win, insist_win/10000.0))
print("换门,赢的概率 %d/10000 = %.2f"%(change_win, change_win/10000.0))
调试记录:
Microsoft Windows [版本 6.1.7601]
版权所有 (c) 2009 Microsoft Corporation。保留所有权利。
C:\Users\Administrator>cd C:\20230516使用python3确认三门问题
C:\20230516使用python3确认三门问题>python 3door3.py
不换门,赢的概率 3302/10000 = 0.33
换门,赢的概率 6711/10000 = 0.67
C:\20230516使用python3确认三门问题>python 3door3.py
不换门,赢的概率 3330/10000 = 0.33
换门,赢的概率 6714/10000 = 0.67
C:\20230516使用python3确认三门问题>python 3door3.py
不换门,赢的概率 3347/10000 = 0.33
换门,赢的概率 6735/10000 = 0.67
C:\20230516使用python3确认三门问题>
参考资料:
https://blog.csdn.net/weixin_41763756/article/details/90756665
三门问题的Python验证
# coding=gbk
"""
三门问题简述:三个门后边有两只山羊,一部汽车,顾客开始选择任意一个门,然后主持人打开存有山羊的一个门,如果改变选择,它的概率是多少选中车
"""
import random
i=0
count=0
doors=["s","s","c"] #分别代表车,与山羊
# 蒙特卡洛方法的应用,三门问题从理论上探讨是十分困难的,但是蒙特卡洛方法给我们一种验证的方法
while i<=1000:
# 随机洗牌,打乱顺序返回自身
random.shuffle(doors)
# 利用列表索引来代表不同的门牌的选择
first_choice=random.randint(0,2)
# 首先从用遍历找到不是车的所有索引集合,在随机抽取一下,模仿从主持人所做的动作
masetchoices=[]
for j in range(3):
if doors[j]!="c":
masetchoices.append(j)
masetchoice=random.choice(masetchoices)
# 改变选择就是,遍历索引是的,最后选择的索引不在前两个之中就可以,若是在这个条件下,改索引获得车,就是胜利,可以计数加1
for z in range(3):
if z not in[first_choice,masetchoice]:
if doors[z]=="c":
count+=1
i=i+1
print(count/1000)
调试记录:
C:\20230516使用python3确认三门问题>
C:\20230516使用python3确认三门问题>python 3door1.py
File "3door1.py", line 1
SyntaxError: Non-UTF-8 code starting with '\xa1' in file 3door1.py on line 1, but no encoding declared; see http://python.org/dev/peps/pep-0263/ for details
C:\20230516使用python3确认三门问题>python 3door1.py
File "3door1.py", line 2
“”“
^
SyntaxError: invalid character in identifier
C:\20230516使用python3确认三门问题>python 3door1.py
File "3door1.py", line 4
三门问题简述:三个门后边有两只山羊,一部汽车,顾客开始选择任意一个门,然后主持人打开存有山羊的一个门,如果改变选择,它的概率是多少选中车
""""
^
SyntaxError: EOL while scanning string literal
C:\20230516使用python3确认三门问题>python 3door1.py
File "3door1.py", line 7
doors=["s","s","c"]#分别代表车,与山羊
^
SyntaxError: invalid character in identifier
C:\20230516使用python3确认三门问题>python 3door1.py
Traceback (most recent call last):
File "3door1.py", line 11, in <module>
random.shuffle(doors)
NameError: name 'random' is not defined
C:\20230516使用python3确认三门问题>python 3door1.py
0.651
C:\20230516使用python3确认三门问题>python 3door1.py
0.673
C:\20230516使用python3确认三门问题>python 3door1.py
0.65
C:\20230516使用python3确认三门问题>python 3door1.py
0.684
C:\20230516使用python3确认三门问题>
https://blog.csdn.net/qq_45757739/article/details/108624679
“三门问题”详解以及python验证
# coding=gbk
# Created with Python AI
from random import choice
def stay():
Choose=choose
return Choose
def switch():
doors.remove(choose)
doors.remove('empty')#只会删除一个empty
Choose = doors
return Choose
if __name__ == '__main__':
cout_stay = 0 #初始化
win_stay = 0
cout_switch = 0
win_switch = 0
decision=['stay','change']
for i in range(100000): #设置模拟次数
doors=['Ferrari','empty','empty']#设置门,无ABC顺序
choose=choice(doors)
if choice(decision) == 'stay':
cout_stay += 1
if stay() == 'goat':
win_stay +=1
else:
cout_switch +=1
if switch() == ['Ferrari']:
win_switch +=1
print(f'''更换后选到法拉利的概率为{win_switch/cout_switch}
''')
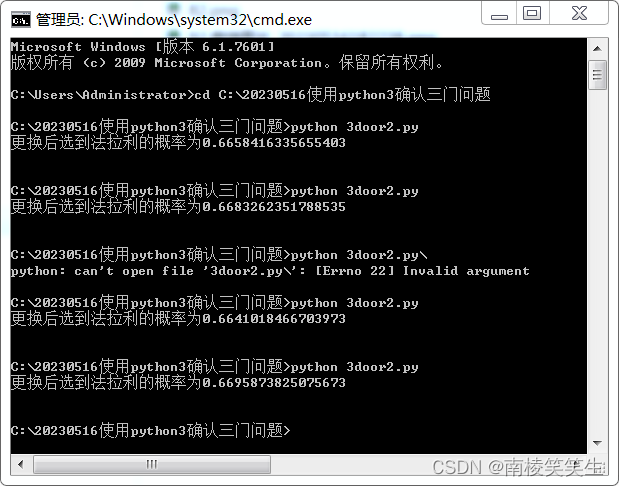
调试记录:
Microsoft Windows [版本 6.1.7601]
版权所有 (c) 2009 Microsoft Corporation。保留所有权利。
C:\Users\Administrator>cd C:\20230516使用python3确认三门问题
C:\20230516使用python3确认三门问题>python 3door2.py
更换后选到法拉利的概率为0.6658416335655403
C:\20230516使用python3确认三门问题>python 3door2.py
更换后选到法拉利的概率为0.6683262351788535
C:\20230516使用python3确认三门问题>python 3door2.py\
python: can't open file '3door2.py\': [Errno 22] Invalid argument
C:\20230516使用python3确认三门问题>python 3door2.py
更换后选到法拉利的概率为0.6641018466703973
C:\20230516使用python3确认三门问题>python 3door2.py
更换后选到法拉利的概率为0.6695873825075673
C:\20230516使用python3确认三门问题>
https://www.jianshu.com/p/b45e6a148663
Python验证三门问题
https://wenku.baidu.com/view/fd019148bb4ae45c3b3567ec102de2bd9605de6c.html
关于三门问题的Python代码
https://baijiahao.baidu.com/s?id=1762600900513206297&wfr=spider&for=pc
最烧脑的悖论,意识为什么会影响未来?颠覆你认知的三门问题