目录
深度优先搜索
概念
图解过程
伪代码
时间复杂度
具体代码(C语言)
广度优先搜索
概念
图解过程
伪代码
时间复杂度
具体代码(C语言)
为什么需要两种遍历
图不连通怎么办
连通
路径
回路
连通图
连通分量
强连通
强连通图
强连通分量
解决-C语言
深度优先搜索
概念
深度优先搜索(Depth First Search,DFS)
在图G中任选一顶点v为初始出发点(源点),则深度优先遍历可定义如下:
首先访问出发点v,并将其标记为已访问过;
然后依次从v出发搜索v的每个邻接点w。
若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。
若此时图中仍有未访问的顶点,则返回去另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
类似于树的先序遍历,例如要深度优先遍历下面的一个图:
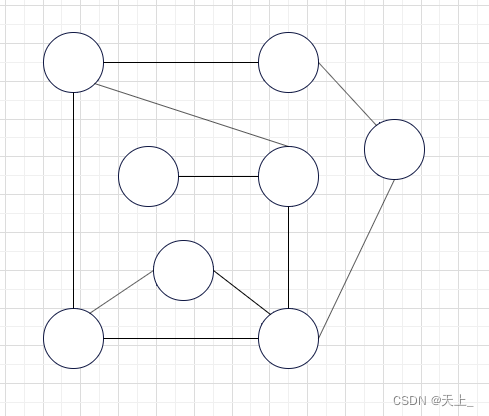
图解过程
具体的一个过程如下:
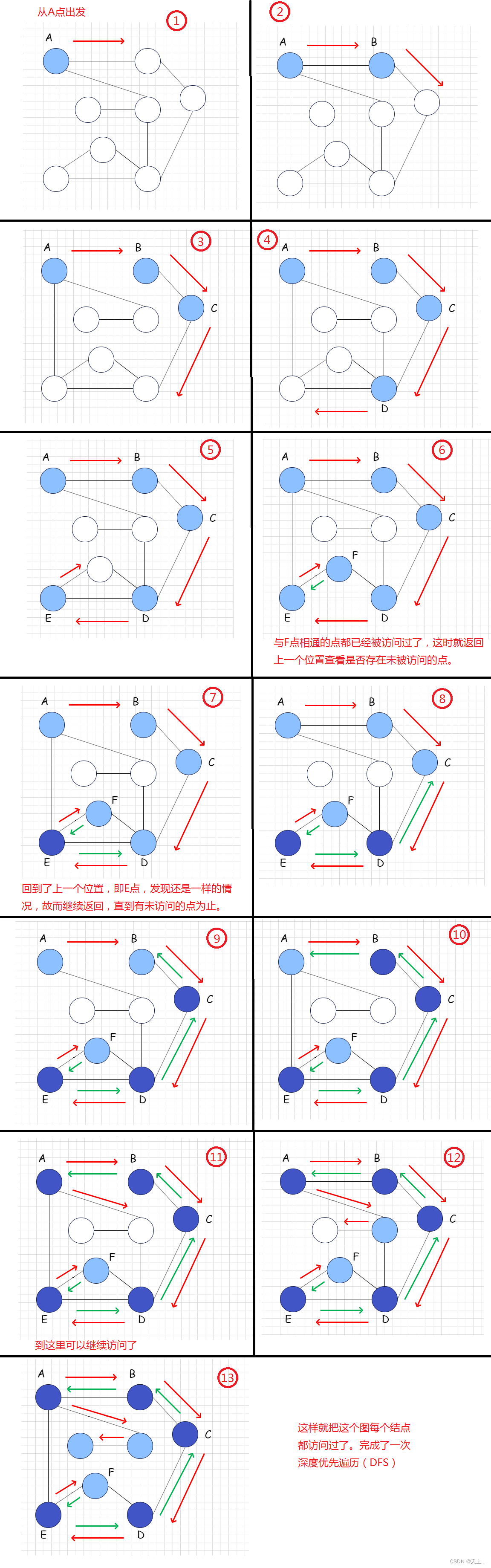
伪代码
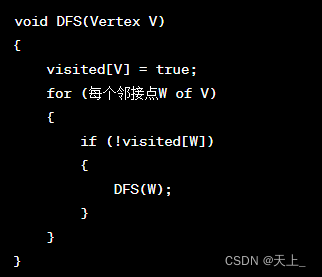
时间复杂度
若有N个顶点、E条边,时间复杂度是:
- 用邻接表存储图,为O(N+E)
- 用邻接矩阵存储图,为O(N的平方)
具体代码(C语言)
#define MAX_VERTICES 100
int visited[MAX_VERTICES];
typedef struct Node
{
int vertex;
struct Node* next;
} Node;
// 深度优先遍历图函数
void DFS(Node* graph[], int v)
{
visited[v] = 1; // 标记当前顶点为已访问
printf("%d ", v); // 输出当前访问的顶点
Node* current = graph[v]; // 获取当前顶点的邻接链表头节点
while (current != NULL)
{
int adjacentVertex = current->vertex; // 获取当前邻接顶点
if (!visited[adjacentVertex])
{
DFS(graph, adjacentVertex); // 递归调用DFS,遍历邻接顶点
}
current = current->next; // 继续处理下一个邻接顶点
}
}广度优先搜索
概念
广度优先搜索(Breadth First Search,BFS)
它从图中的某个顶点开始遍历,先访问它的所有邻接顶点,然后再逐层遍历下去,直到图中所有顶点都被访问到为止。
就类似于树的层序遍历,一样是通过队列来实现,再取之前那个图:

图解过程
具体遍历过程:
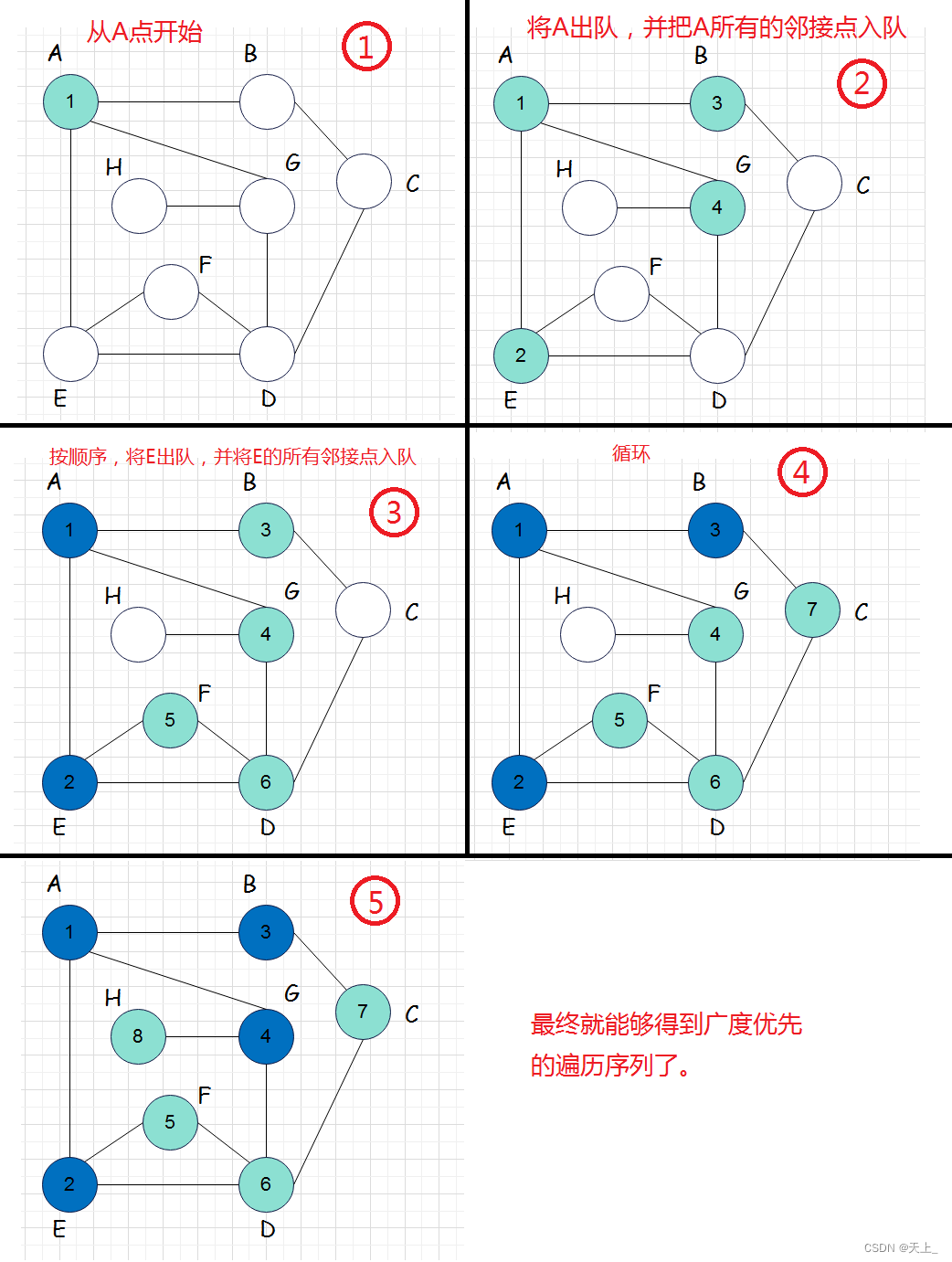
伪代码
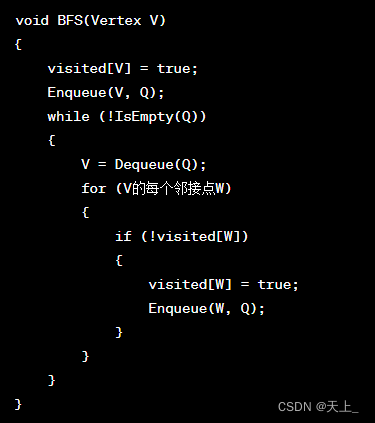
时间复杂度
若有N个顶点、E条边,
- 用邻接表存储图,时间复杂度为O(N+E)
- 用邻接矩阵存储图,有O(N的平方)
具体代码(C语言)
#define MAX_VERTICES 100 // 最大顶点数
// 广度优先搜索函数
void BFS(Vertex V, Vertex* adjacencyList[])
{
bool visited[MAX_VERTICES]; // 记录顶点是否已访问
Queue* Q = createQueue(); // 创建一个队列用于存储待访问的顶点
// 初始化visited数组为false,表示所有顶点都未被访问
for (int i = 0; i < MAX_VERTICES; i++)
{
visited[i] = false;
}
visited[V] = true; // 标记起始顶点V为已访问
enqueue(Q, V); // 将起始顶点V入队
while (!isEmpty(Q))
{
V = dequeue(Q); // 从队列中取出一个顶点V
// 遍历V的每个邻接点W
Vertex* adjVertex = adjacencyList[V]; // 获取顶点V的邻接点链表头指针
while (adjVertex != NULL)
{
int W = adjVertex->data; // 获取邻接点W的数据
if (!visited[W])
{
visited[W] = true; // 标记顶点W为已访问
enqueue(Q, W); // 将顶点W入队
}
adjVertex = adjVertex->next; // 遍历下一个邻接点
}
}
}
Vertex* adjacencyList[]参数表示图的邻接表,以便获取顶点V的邻接点链表头指针。在
内部的while循环中,使用adjVertex指针遍历顶点V的邻接点链表,获取每个邻接点W的数据,并进行相应的操作。
为什么需要两种遍历
我们可以用走迷宫的方式来解释为什么需要两种遍历方式。
假设我们有一个迷宫,迷宫可以看作是一个图形数据结构,其中每个房间都是一个节点,房间之间的通道则是边。
深度优先遍历(DFS)
当我们使用深度优先遍历时,我们会选择一条路径,沿着这条路径尽可能远地探索下去,直到无法继续为止,然后返回上一层节点继续探索。
换在迷宫中,就意味着我们会选择一个通道,并一直走到无法再走下去为止,然后返回到上一个房间,继续选择下一个可行的通道进行探索。
这样就会导致,我们会沿着一个路径一直走到底,直到找到解决问题的目标或者无路可走。
DFS的特点是适合深度探索,对于搜索路径较深的问题很有效。
广度优先遍历(BFS)
与DFS不同,广度优先遍历是逐层扩展。
我们从起点开始,首先探索与起点直接相邻的节点,然后再探索与这些节点相邻的节点,以此类推,直到找到解决问题的目标或者遍历完整个图。
在迷宫中,我们先选择起点的所有相邻房间,然后再选择这些房间的所有相邻的房间,以此类推。这样做的结果是,我们会逐层地扩展搜索,确保我们在搜索过程中覆盖了所有可能的路径。
BFS的特点是适合寻找最短路径或者层次遍历问题。
所以,DFS和BFS在处理图形数据结构时具有不同的特点和应用场景。DFS适合深度探索和回溯问题,而BFS适合寻找最短路径或者层次遍历问题。根据具体的问题需求,我们可以选择适合的遍历方式来解决。
图不连通怎么办
连通
如果从V到W存在一条(无向)路径,则称V和W是连通的。
路径
V到W的路径是一系列顶点{V,V1,V2,...,Vn,W}的集合,其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数(如果带权,则是所有边的权重和)。如果V到W之间的所有顶点都不同,则称简单路径。
回路
起点等于终点的路径。
连通图
图中任意两顶点均连通。
连通分量
无向图的极大连通子图。
- 极大顶点数:以原来的图为来源,再加1个顶点就不连通了。
- 极大边数:包含子图中所有顶点相连的所有边。
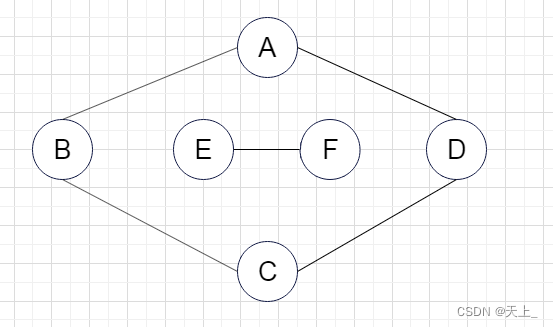
根据上面这个图,我们来判断一下以下是否是其连通分量:
(一)
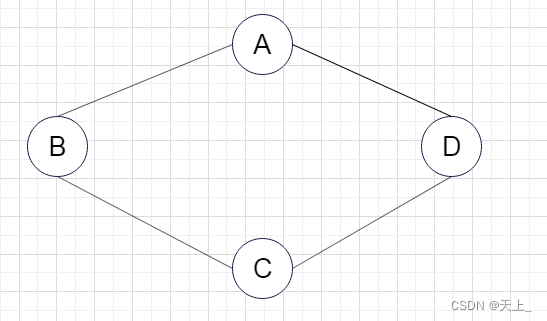
是其连通分量,因为包含了子图中所有顶点相连的边,而且再加一个顶点就不能连通了,例:
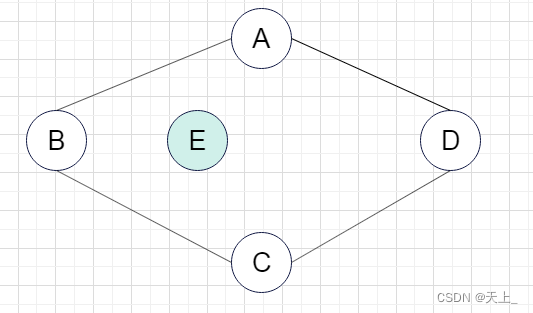
(二)
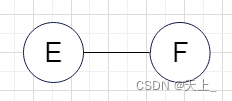
是其连通分量 ,与(一)类似。
(三)
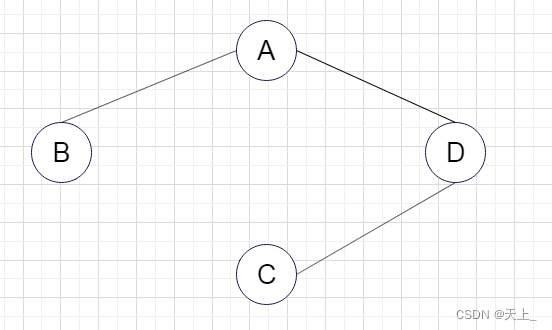
不是其连通分量 ,不包含子图中所有顶点相连的边。
(四)
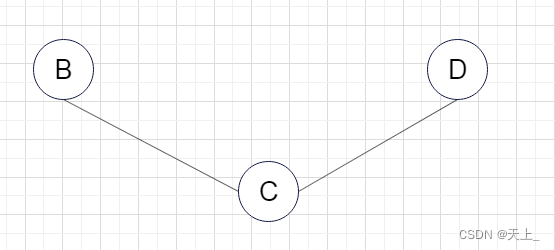
不是其连通分量 ,虽然包含了子图所有顶点相连的边,但是不满足极大顶点数,加入A点之后还是连通的。
强连通
有向图中顶点v和w之间存在双向路径,则称v和w是强连通的。
强连通图
有向图中任意两顶点均强连通。
强连通分量
有向图的极大强连通子图。
强连通图:
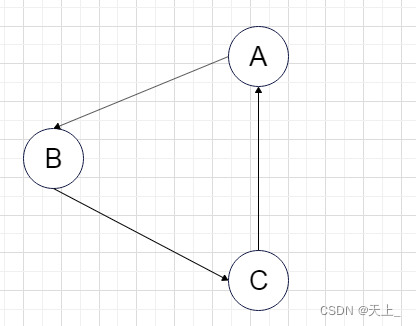
强连通分量:
在图G中,
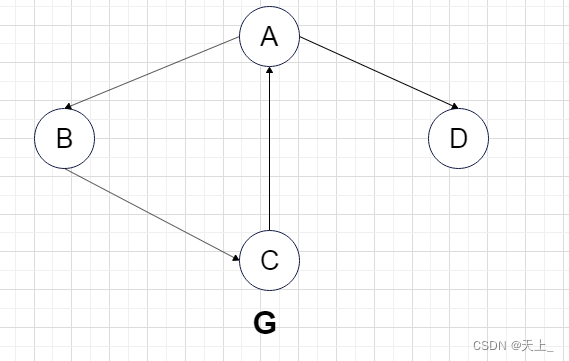
它的强连通分量是:
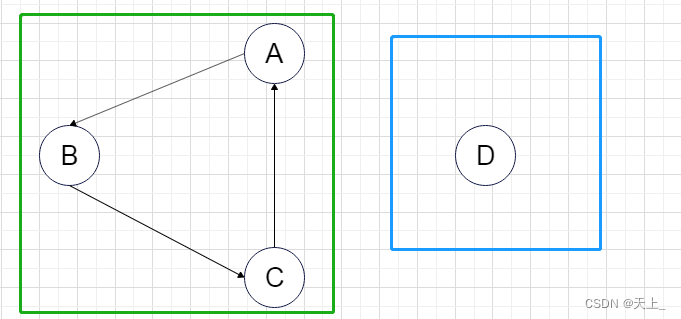
解决-C语言
#define MAX_VERTICES 100 // 最大顶点数
// 定义图
typedef struct Graph
{
int numVertices;
Node* adjacencyList[MAX_VERTICES];
int visited[MAX_VERTICES];
} Graph;
// 遍历所有连通分量
void ListComponents(Graph* graph)
{
int i;
for (i = 0; i < graph->numVertices; ++i)
{
if (!graph->visited[i])
{
DFS(graph, i);
}
}
}end
学习自:MOOC数据结构——陈越、何钦铭