使用Vue+Python基于卷积神经网络前后端分离实现蔬菜种类预测系统

一、实现效果

1、种类预测界面

2、数据处理分析界面

3、网络模型界面

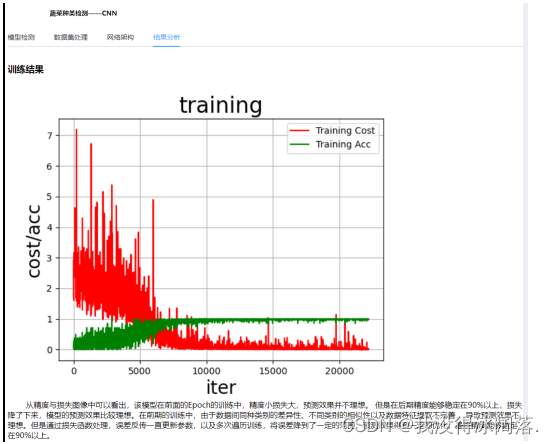
4、结果分析界面

二、需求分析

用户通过上传待预测图片到系统，系统预测出该图片对应的蔬菜种类，并且提示用户预测信息。系统需要对预测模型、数据处理过程以及结果预测分析，并将分析的结果反馈用户，方便用户查看。

三、主要设计

1、基本要求

该系统以卷积神经网络为模型，前端界面使用Vue实现，FastApi为后端服务器，实现水果品种分类预测。前端通过上传待预测图片到服务器后，利用已经训练好的模型，预测该图片对应蔬菜品种，准确率能达到90%。系统还实现模型架构分析、数据处理分析以及结果分析功能。

2、数据预处理分析

该模型数据集为生活中常见12类蔬菜图片，对应种类模型预测界面均有简介。图片通过上网爬取，每类图片大约有400多张，每张图片均为JPG格式图片。

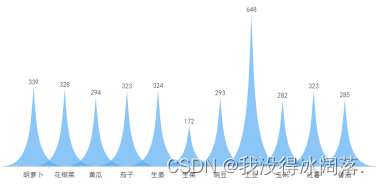
数据集处理包含以下特点：

• 从数据集中随机挑选一部分做测试集，训练集测试集比例为9:1
• 数据集文件夹子文件夹名称作为键，以递增数字为值，建立类别字典
• 将训练集、测试集中图片位置与对应类别分别存入文本中，便于图片读取
• 网络输入为128*128,对每张图片做归一化处理

3、网络模型

卷积层与池化层

• 网络模型中，图像输入大小为128x128，维度为三维
• 第1个卷积层卷积核大小为5x5，维度为32维，经过第1个卷积块卷积后，输出图像为124x124x32；在卷积层后经过最大池化，输出图像为62x62x32
• 第2个卷积层卷积核大小为3x3，维度为64维， 经过第2个卷积块卷积后，输出图像为60x60x64；在卷积层后经过最大池化，输出图像为30x30x64
• 第3个卷积层卷积核大小为3x3，维度为64维，经过第1个卷积块卷积后，输出图像为28x28x64；在卷积层后经过最大池化，输出图像为14x14x64

全连接层

• 第一个全连接层为2048
• 第二个全连接层为512
• 最后输出结果经过softMax函数回归，得到12个种类可能概率

激活函数

Relu函数表达式为f(x)=max(0,x)。作为激活函数，relu计算简单，更加高效，速度快；在优化时，不像Sigmoid型函数的两端饱和（两端的梯度都接近0）， ReLU函数为左饱和函数，且在x> 0 时导数为1，而且导数也好求，在一定程度上能解决梯度消失的问题，加速梯度下降的收敛速度。

损失函数-交叉熵损失函数

• 交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中就表示为真实概率分布与预测概率分布之间的差异
• 交叉熵的值越小，模型预测效果就越好
• 熵经常搭配softmax使用，将输出的结果进行处理，使其多个分类的预测值和为1，再通过交叉熵来计算损失

四、详细设计

CNN 在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，而不需要任何输入和输出之间的精确的数学表达式，只要用已知的模式对卷积网络加以训练，网络就具有输入输出对之间的映射能力。

卷积网络执行的是监督训练，所以其样本集是由形如：（输入向量，理想输出向量）的向量对构成的。所有这些向量对，都应该是来源于网络即将模拟系统的实际“运行”结构，它们可以是从实际运行系统中采集来。

1）参数初始化：
在开始训练前，所有的权都应该用一些不同的随机数进行初始化。
“小随机数”用来保证网络不会因权值过大而进入饱和状态，从而导致训练失败；
“不同”用来保证网络可以正常地学习。实际上，如果用相同的数去初始化权矩阵，则网络无学习能力。

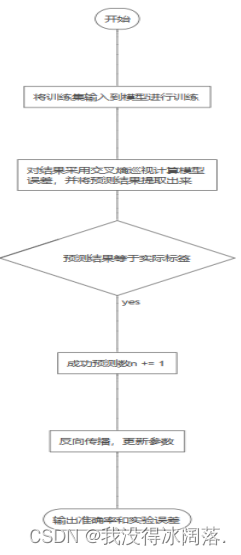
2）训练过程包括四步

① 第一阶段：前向传播阶段
从样本集中取一个样本，输入网络

计算相应的实际输出；在此阶段信息从输入层经过逐级的变换，传送到输出层，这个过程也是网络在完成训练之后正常执行时执行的过程

② 第二阶段：后向传播阶段

计算实际输出与相应的理想输出的差

按照极小化误差的方法调整权值矩阵

网络的训练过程如下：

选定训练组，从样本集中分别随机地寻求 N 个样本作为训练组；

将各权值、阈值，置成小的接近于 0 的随机值，并初始化精度控制参数和学习率；

从训练组中取一个输入模式加到网络，并给出它的目标输出向量；

计算出中间层输出向量，计算出网络的实际输出向量；

将输出向量中的元素与目标向量中的元素进行比较，计算出输出误差；对于中间层的隐单元也需要计算出误差；

依次计算出各权值的调整量和阈值的调整量；

调整权值和调整阈值；

当经历 M 后，判断指标是否满足精度要求，如果不满足，则返回 (3)，继续迭代；如果满足就进入下一步；
训练结束，将权值和阈值保存在文件中。这时可以认为各个权值已经达到稳定，分类器已经形成。再一次进行训练，直接从文件导出权值和阈值进行训练，不需要进行初始化。

五、结果分析

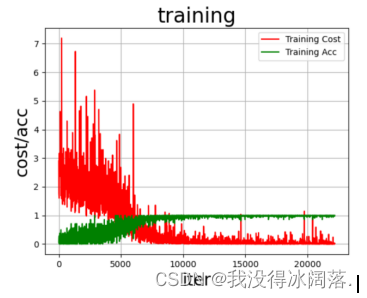
从精度与损失图像中可以看出，该模型在前面的Epoch的训练中，精度小损失大，预测效果并不理想。但是在后期精度能够稳定在90%以上，损失降了下来，模型的预测效果比较理想。在前期的训练中，由于数据间同种类别的差异性、不同类别的相似性以及数据特征提取不完善，导致预测效果不理想。但是通过损失函数处理，误差反传一直更新参数，以及多次遍历训练，将误差降到了一定的范围，预测效果得到一定的优化，最终精度能够稳定在90%以上。