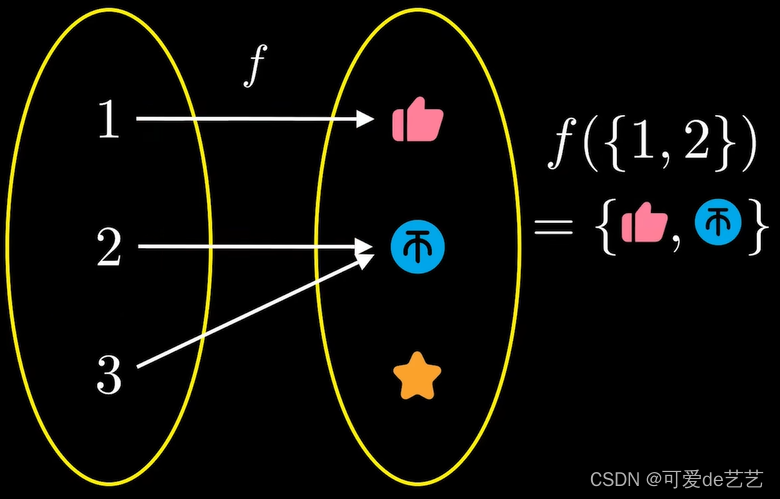
映射的概念:有两个集合A,B，若A的任何元素都有唯一的B中元素与之对应，B中元素与之对应的称为像，A中对应的元素称为原像

 

一个集合也有像，定义为各自像的集合

 

B中集合也有原像，定义为各自原像的集合

 

虽然采用了f-1的符号，但不代表f是可逆的，同时也有定义域和值域的概念

可以看到，A中是不能有闲置元素的，而B可以有，换句话说，值域的B的一个子集

当B没有闲置元素时，f被称为满射，此时A的元素比B只多不少

 

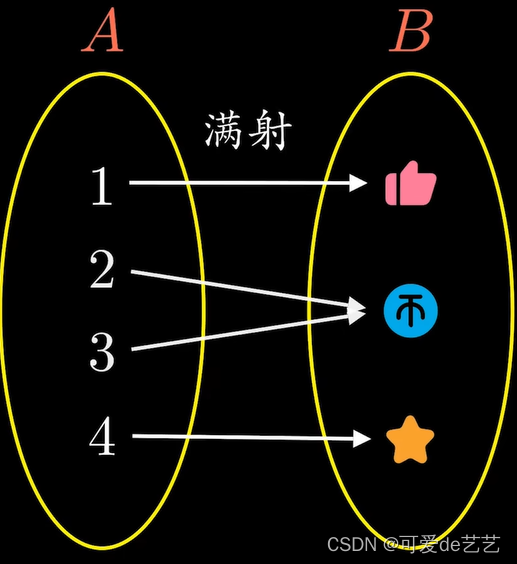
当A中不同元素的像不同时，f称为单射

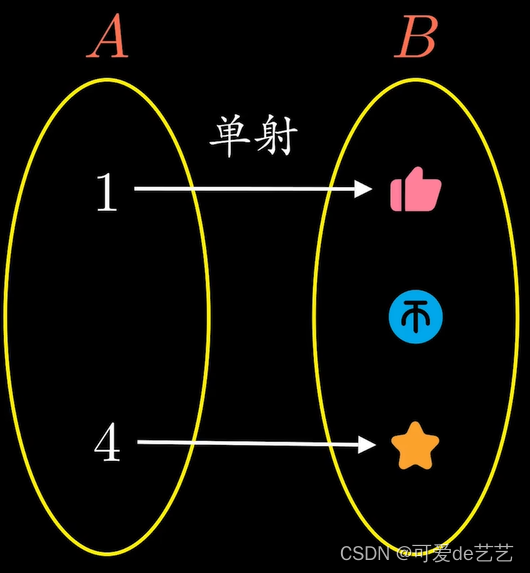
 此时A的元素只比B只少不多

若f同时是单射和漫射，称f为双射或一一映射，此时A与B元素一样多

若为f为双射，可以保证f可逆

 

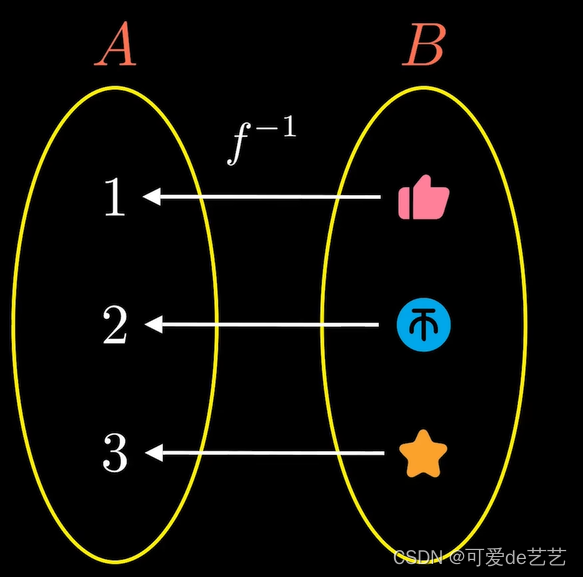
若f是B到C的一个映射，而g的值域又包含在B中，则可以将f和g复合

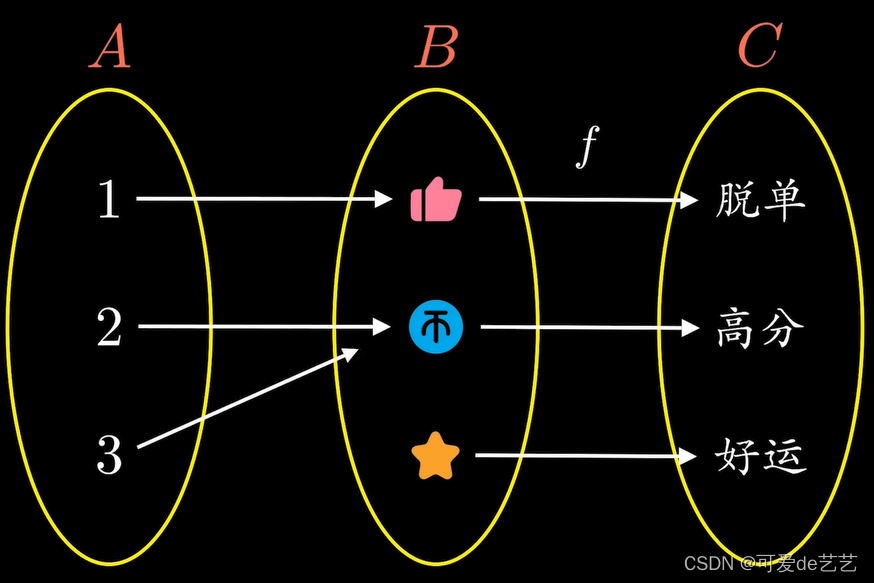
 一般来说映射不符合交换律，但一定符合结合律

f和f-1的复合称为恒等映射