前面的文章中我们简单的实现了一个红黑树，实现了它的插入的功能，在本文中我们来对其进行修改并构建Set与Map。
下面我们来从源码中截取一点有关Map与Set的代码；
可以看出，在STL30中构建Map与Set使用的是同一个红黑树模板，只是传入了不同的参数。然后我们再来看一下里面红黑树的一些代码，可以看出在set中传入了两个key，在map中传入了一个key一个pair。
set<K> -> rb_tree<K，K>
map<K，V> -> rb_tree<K，pair<const K，V>>
第一个模板参数单独拿到K的类型，因为find与erase这些接口函数参数是K；
第二个模板参数决定了树的节点里面存储了什么类型的数据。
下面我们来进行封装：
仿函数
将结点先存储的数据从pair变为模板类型T；
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};然后我们会遇到的问题就是在插入中，之前我们使用的是pair类型的数据，因此插入取的值为kv.first；但是由于Map与Set需要对红黑树的模板进行复用，在红黑树中我们树不清楚使用该模板的到底是Map还是Set，但是在上一层中就可以获取这个消息，所以这里就需要我们引入一个仿函数，通过在Map与Set中仿函数传入红黑树中来获取Set与Map中的K值，这样我们就可以使用K值来进行比较。
struct MapKeyOfT
{
const K& operator()(const pair<const K, V>& kv)
{
return kv.first;
}
};
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
除了上面的，我们还可以编写仿函数来控制Map与Set的数据插入的策略。
迭代器
下面我们来继续看一下迭代器
迭代器也与我们之前学习的链表的迭代器相类似不过多赘述，下面我们来讲解一下红黑树迭代器特有的部分，迭代器的++与--如何实现：红黑树要走中序，begin()位置的结点就是整棵树最左边的结点返回的地址，end结点在这里我们取的是空节点。
typedef __RBTreeIterator<T, T&, T*> itertaor;
typedef __RBTreeIterator<T, const T&, const T*> const_itertaor;
itertaor begin()
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return itertaor(cur);
}
itertaor end()
{
return itertaor(nullptr); // end是最后一个节点的下一个数据
}
在这里编写迭代器的时候还需要注意一点就是：取类模板的内嵌类型需要添加typename，否则编译器不知道这个是类型还是静态变量。
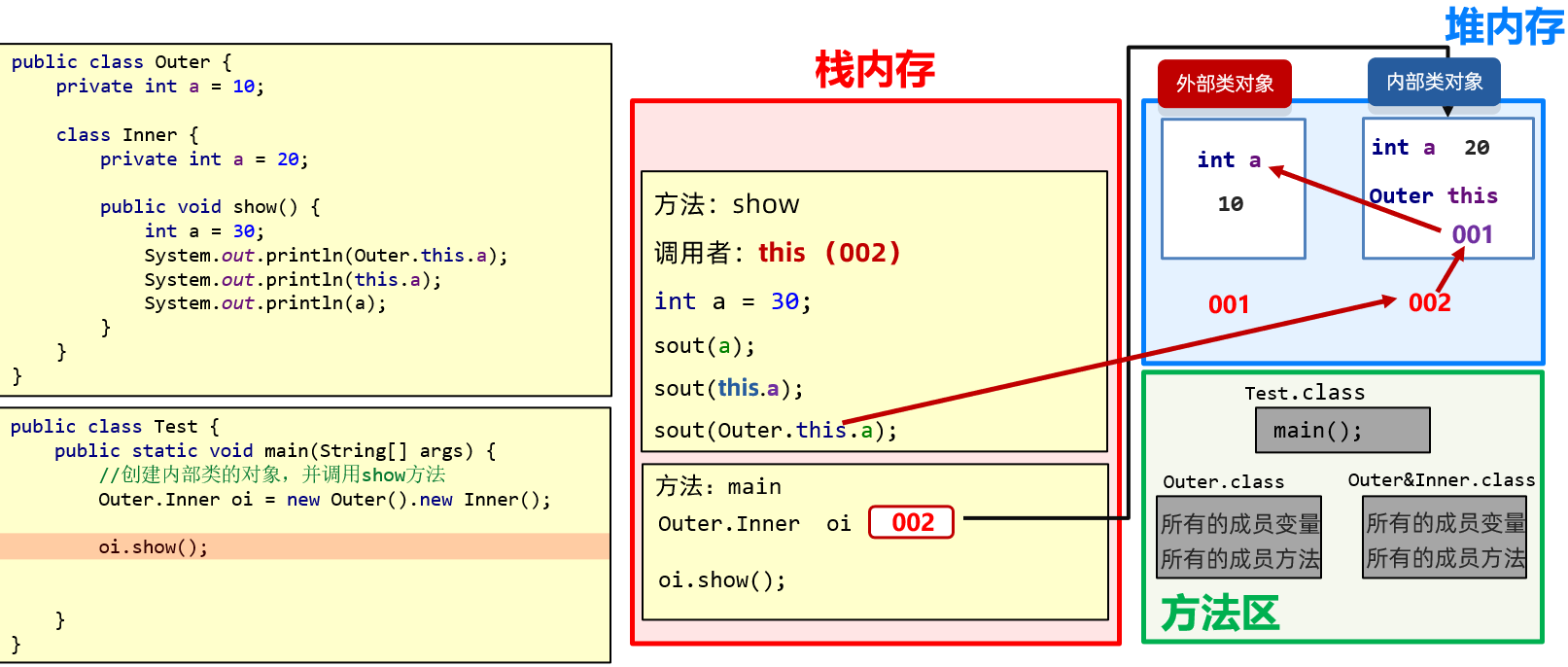
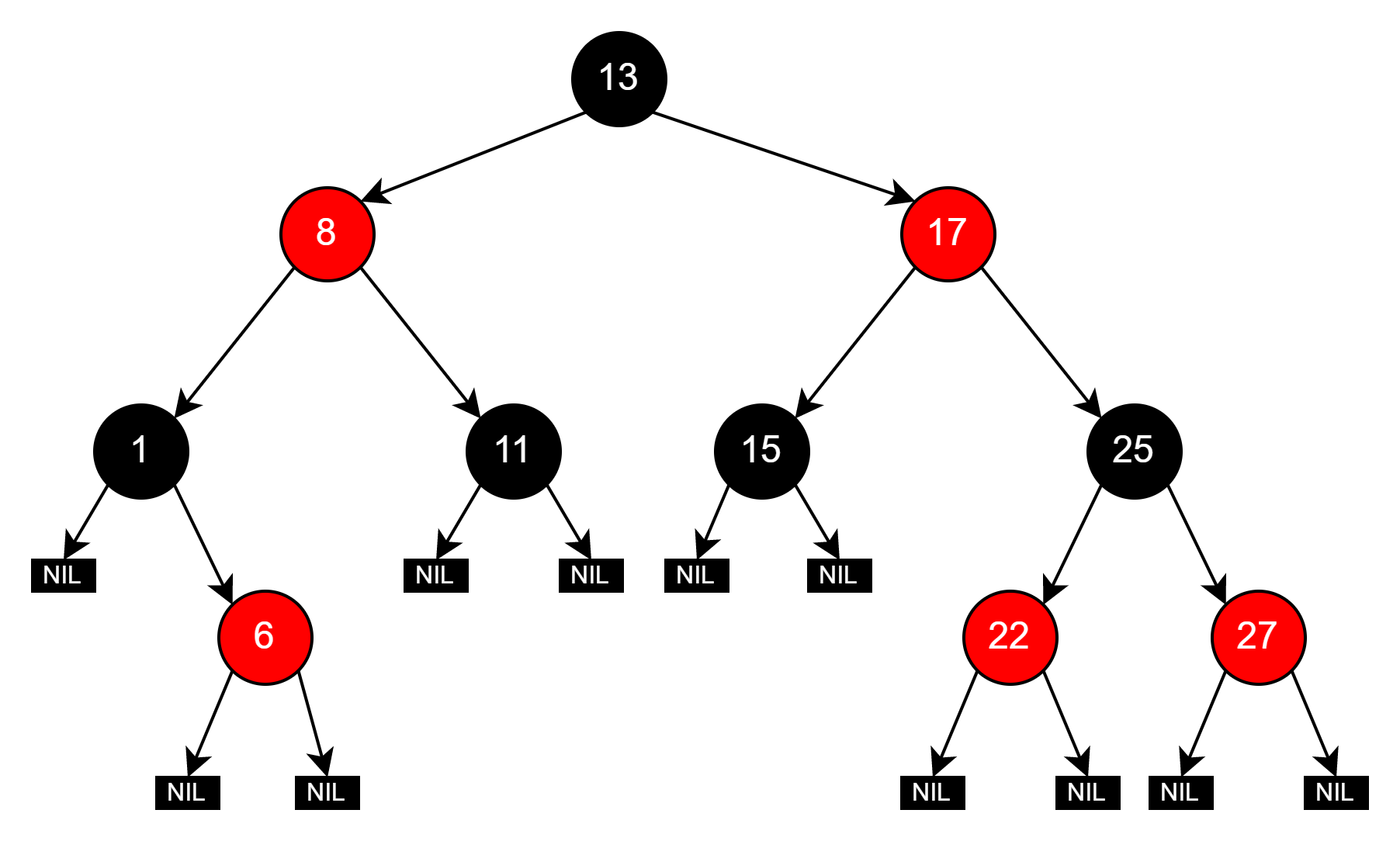接着我们继续编写++的代码， 以上图为例子，当处于1号节点的时候已经处于最左的结点，下一步就是寻找右子树的最左结点。
if (_node->_right)
{
// 右不为空，下一个就是右子树的最左节点
Node* subLeft = _node->_right;
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
_node = subLeft;
}
然后就是当右子树为空时，此时如果该节点是父亲的左节点，那么下一个结点就是父亲节点，如果该节点是父亲的右节点，那么说明父亲这棵子树全部遍历完毕，下一个节点就是祖父节点。
else
{
// 右子树为空，沿着根的结点，找孩子是父亲左的那个祖先
Node* parent = _node->_parent;
while (parent && _node == parent->_right)
{
_node = parent;
parent = parent->_parent;
}
_node = parent;
}
有++的话--也是同样的方法，通过右子树 根 左子树的顺序进行遍历，就可以得到--的效果。
Map中[]的重载
在Map中还有着[]的方法，使用[]的操作是，如果没有该数据就可以将该数据的key值进行插入，如果有该数据，就可以返回该数据的key值对应的value值。在红黑树中就需要对插入的返回值进行修改变为 pair<iterator, bool> 类型，然后就可以使用Map对[]进行重载。
V& operator[](const K& key)
{
pair<iterator, bool> ret = _t.Insert(make_pair(key, V()));
return ret.first->second;
}
Set中的使用普通迭代器构造const迭代器
在Set中还有这这样的一个问题，当我们使用const迭代器的时候我们是无法对key的值进行修改的，这是我们都知道的，但是当我们使用普通迭代器的时候却发现在这个key值，能够被修改。这种情况是不正确的，因此就可以使用const迭代器来构建普通迭代器，但此时就会有一个问题：
错误 C2440 “return”: 无法从“std::pair<__RBTreeIterator<T,T &,T *>,bool>”转换为“std::pair<__RBTreeIterator<T,const T &,const T *>,bool>”
这是因为在我们的红黑树代码中只有下面的构造函数，
__RBTreeIterator(Node* node)
:_node(node)
{}当构建迭代器的begin的时候返回值是一个const迭代器，而return的只是一个普通的迭代器，因此就会发生报错。
const_iterator begin() const
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}所以我们可以在红黑树中这样来编写代码：
typedef __RBTreeIterator<T, Ref, Ptr> Self;
typedef __RBTreeIterator<T, T&, T*> iterator;
typedef __RBTreeIterator<T, const T&, const T*> const_iterator;
__RBTreeIterator(const iterator& it)
:_node(it._node)
{}
分别初始化一个普通迭代器，一个const迭代器和Self，并且编写下面的构造函数，当迭代器是普通迭代器的时候下面的构造函数就是一个拷贝构造函数，当迭代器是const迭代器的时候下面的构造就是一个普通的构造函数，使用迭代器来构造const迭代器。从而可以达到上述的效果。
