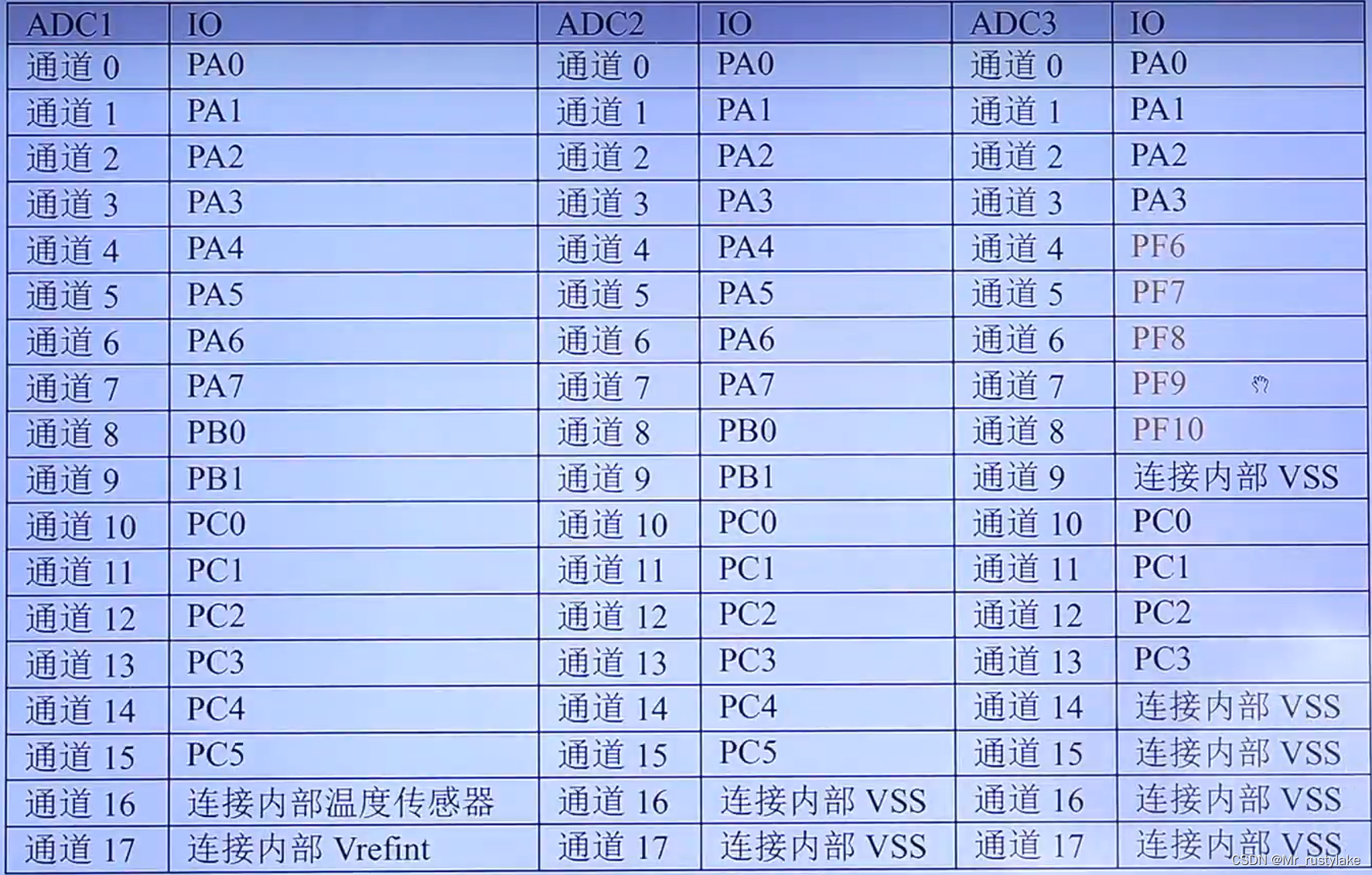
文章目录
- 1. 题目描述
- 2. 解题思想
- 3. 设置dp初始值
- 4.代码实现
1. 题目描述

2. 解题思想
- 定义dp数组
dp[i][j]:表示当字符串长度i,j是,s与p是否匹配
- 确定递推公式
核心是s[i]要与p[j]进行比较,比较的结果来确定dp数组的值,分为下面几种情况:
(1) 当p[j]是普通字符,直接与s[i]比较,比较的结果就是dp[i][j]的值,这种情况还是比较简单
d p [ i ] [ j ] = { d p [ i ] [ j ] = = d p [ i − 1 ] [ j − 1 ] s [ i ] = = s [ j ] f a l s e s [ i ] ! = s [ j ] dp[i][j]=\begin{cases} dp[i][j]==dp[i-1][j-1]& s[i]==s[j]\\ false & s[i] !=s[j] \end{cases} dp[i][j]={dp[i][j]==dp[i−1][j−1]falses[i]==s[j]s[i]!=s[j]
如下图dp[i][j]的值取决于,s串的i前面的字符串是否于p串的前j个字符匹配(也就是dp[i-1][j-1]),如果s串的i位置于j的p位置的串不匹配,则一定不匹配
(2)如果p[j]是.,则这种情况和第一种情况类似,只是肯定是配置的,不用考虑false的情况,这种情况也很简单
(3)如果p[j]是*,这种情况就比较复杂了,由于*的特性,我们需要考虑*前面的字符
如果
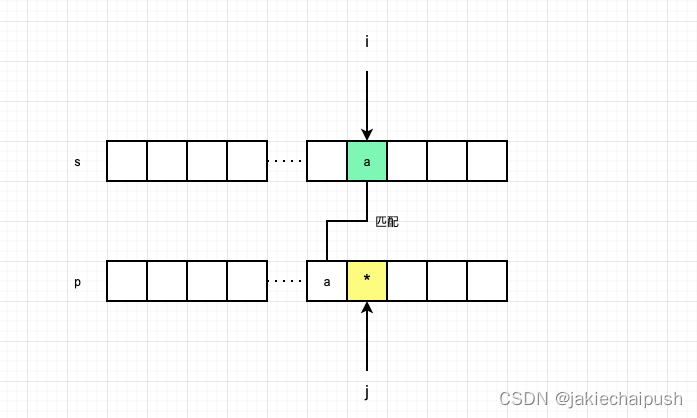
s[i]与*前面一个字符匹配,即s[i]和p[j-1]相同,此时*号才生效,此时*匹配了一个a,如果s[i]和p[j-1]不相同,则此时*失效,它没有代替任何字符,即表示0个字符(此时*和前面的字符都失效)。下面先分析相同的情况,如下图所示:
当
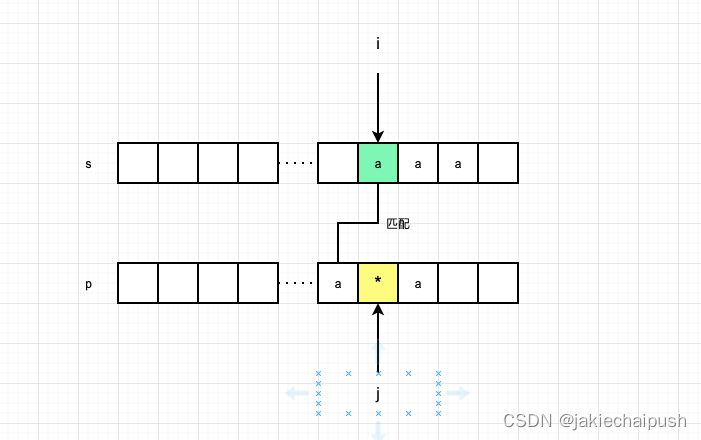
s[i]与s[j]相同,此时*,*可能会和s[i]后面多个与p[j-1]相同的字符匹配,即它可能代表0-n个字符,因为*的匹配个数可能是任意的,考虑下面的情况,此时*只能代表一个字符a。所以我们此时又可以分为三种情况:
- 当
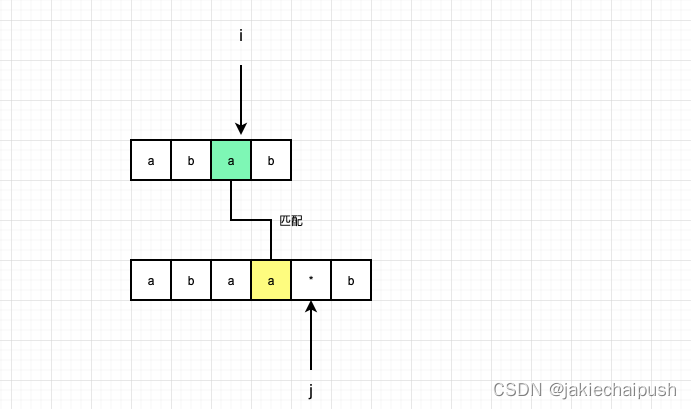
*匹配0个字符,这种情况下,*和前面的字符都失效,如下图的情况,虽然s[i],s[j-1]但*和*前面的字符都是失效的,此时dp[i][j]=dp[i][j-2]
- 当
*匹配一个字符时,如下图,*代表一个a,此时dp[i][j]=dp[i][j-1]
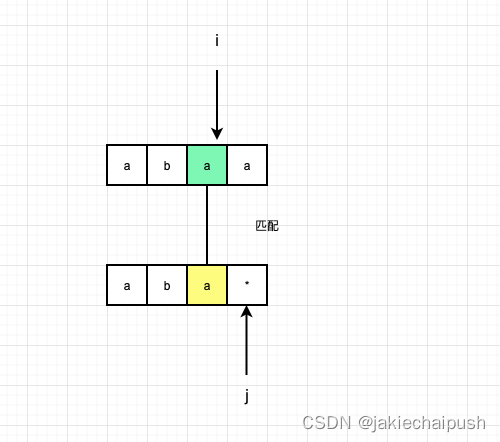
- 当
*匹配多个字符时,如下图,*代表5个a,此时s可以不考虑i后面的a了(相当于i后面所有的a与*抵消了),所以变成了下一张图的情况(虚线表示抵消掉了),此时dp[i][j]=dp[i-1][j]
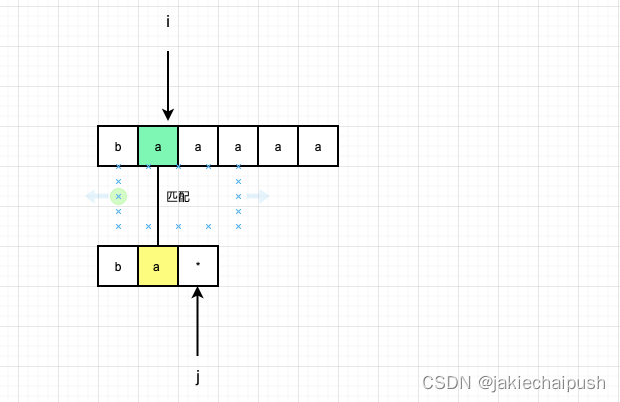
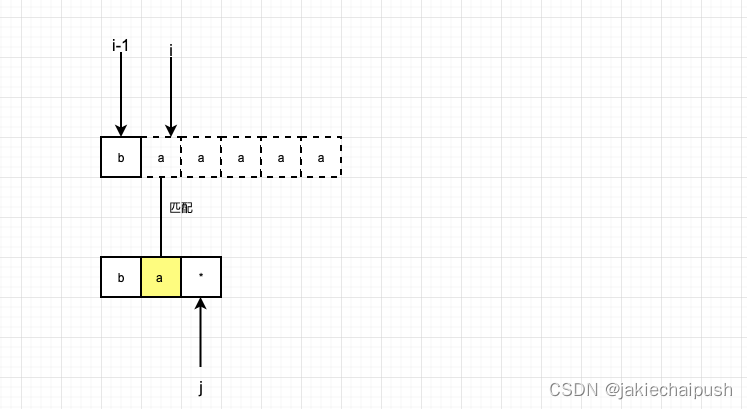
所以我们到底需要匹配0个、1个还是多个,具体选择是根据我们选择能够使整个字符串和正则表达式匹配成功。
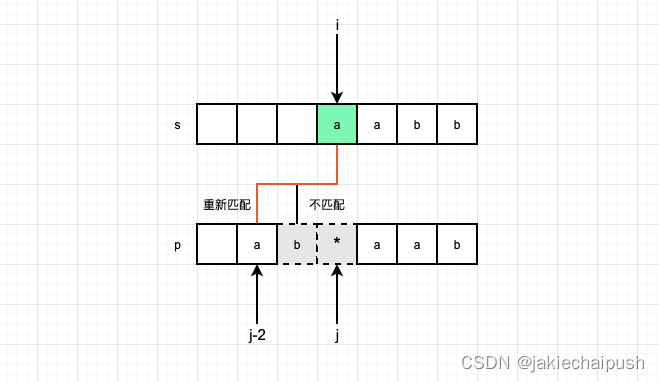
前面分析了
s[i]==p[j-1]的情况,下面分析一下不等于的情况,其实很简单,不相等相当于*与*前面的字符失效了,不参与匹配了而已,此时s[i]还是可以和p[j-2]进行比较的,关键是要认识到字符+*是可有可无的;
3. 设置dp初始值
因为存在
i-1,所以我们的i一定是从1开始的,所以我们要找出dp[0][j]的所有值(这些值不会在遍历种出现
- dp[0][0]=true:
两个字符串都为空,自动匹配成功 - dp[0][1]=false:
s为空,p的长度为1,肯定为false - d p [ 0 ] [ j ] ( j > = 2 ) = { d p [ 0 ] [ j ] = = d p [ 0 ] [ j − 2 ] p [ j ] = = ∗ f a l s e p [ j ] ! = ∗ dp[0][j](j>=2)=\begin{cases} dp[0][j]==dp[0][j-2]& p[j]==*\\ false & p[j] !=* \end{cases} dp[0][j](j>=2)={dp[0][j]==dp[0][j−2]falsep[j]==∗p[j]!=∗
4.代码实现
class Solution{
public boolean isMatch(String s, String p){
//防止空指针,其实根据题目给的参数范围这部分是不需要的
if(s==null || p==null){
return true;
}
//获得两个字符串的长度
int n=s.length();
int m=p.length();
//创建dp数组
boolean[][] dp=new boolean[n+1][m+1]
//下面按照上面介绍的逻辑,初始化dp数组
//两个长度为0的部分默认为true
dp[0][0]=true;
dp[0][1]=false;
for(int j=2;j<=m;j++){
//dp[j-1]为*
if(p.charAt(j-1)=='*'){
dp[0][j]=dp[0][j-2];
}
}
//重点部分
for(int i=1;i <=n ;i++){
//j初始为1不用担心越界(后面存在j-2的情况)是因为*不可能出现在第一个位置
for(int j=1;j<=m;j++){
//当p[j]不为*
if(p.charAt(j-1) !='*){
//当s[i]与s[j]相等或s[j]为.,则匹配成功
if(p.charAt(j-1) == '.'|| s.charAt[i]==p.charAt[j])
{
dp[i][j]=dp[i-1][j-1];
}
else{
dp[i][j]=false;
}
}
//当p[j]为*时
else{
//当s[i]不等于你p[j-1]时(即s[i]和*前的字符不匹配)
if(p.charAt[j-2] !=s.charAt[i] && p.charAt[j-2]!='.')
{
//此时*和*前面的字符失效,相当于从p种踢出,但s[i]还是可以和p[j-2]进行匹配的
dp[i][j]=dp[i][j-2];
}else
{
// 匹配0个或者1个,或者多个 (下面只有一个情况为true,等于为true的那个即可,所以可以用或连接起来
dp[i][j]= dp[i][j-2] || dp[i][j-1] || dp[i-2][j];
}
}
}
}
return dp;
}
}