刚写完了bp神经网络的实验课代码,对这个比较熟悉(后面给出实现代码)
Logistic函数也就是sigmod函数,表达式是这样的:
def sigmod(x):
return 1/(1+math.exp(-x))sigmod函数是隐层和输出层的激活函数(sigmod函数记作f(x),它的导数记作f `(x)),它有一个特点是f `(x)=f(x)*(1 - f(x)),这个特点在推导参数更新公式中有用到。
本题中题干给出的是4X4X3的神经网络,也就是输入层为4,隐层为4,输出层为3。
首先是前向传播过程:
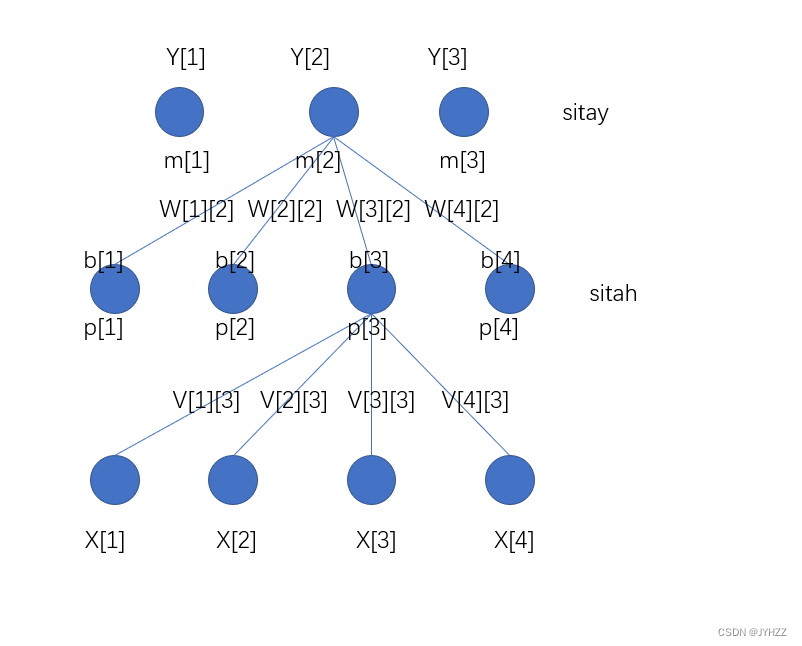
我这里层与层之间的权值只画出了一部分,这里面的某些变量的值和我给出的代码不是一一对应的。
输入层的大小为d=4,输入层下标的变量用i表示
隐层的大小为q=4,隐层下标的变量用h表示
输出层的大小为l=3,输出层下标的变量用j表示
X[i]代表输入的特征
V[i][h]代表输入层和隐层之间的权值
p[h]代表与这个结点相连的4个输入层结点与对应权值v相乘再相加的结果
sitah是隐层结点
b[h]是经过激活函数之后输出的值,即b[h]=sigmod(p[h]-sitah)
W[h][j]是隐层与输出层的权值
m[j]代表与这个结点相连的4个隐层结点与对应权值w相乘再相加的结果
sitay是输出层结点
Y[j]是经过激活函数之后输出的值,即Y[j]=sigmod(m[j]-sitay)
最后我们通过Ek来评估模型输出的好坏:
(括号里面是我们通过训练集计算得的结果减去训练集给出的正确的结果)
推导过程中的注意事项是一个w[h][j]或一个sitay只会影响一个输出值y[j];

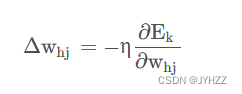
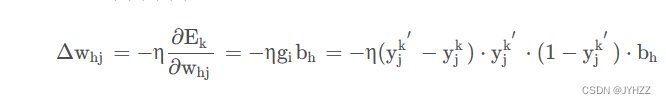
每一个w[h][j]仅会影响与他相连的那唯一一个输出值y[j],其实上面那个公式中的Ek是对全部输出值y[j]来说的,但是我们求的偏导是关于w[h][j],w[h][j]只与y[j]有关系,这样其他的y[1],y[2]啥的无关项就是常数,求偏导就消去了。
sitay同理。
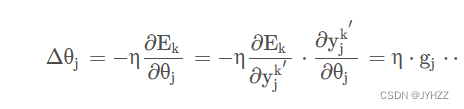
但是一个v[i][h]或者sitah会影响全部的输出值y;
v[i][h]影响所有输出值y的原因是通过v[i][h]计算并激活(用到sitah)得到的b[h],这个b[h]参与到了所有的y的运算中,sitah同理。
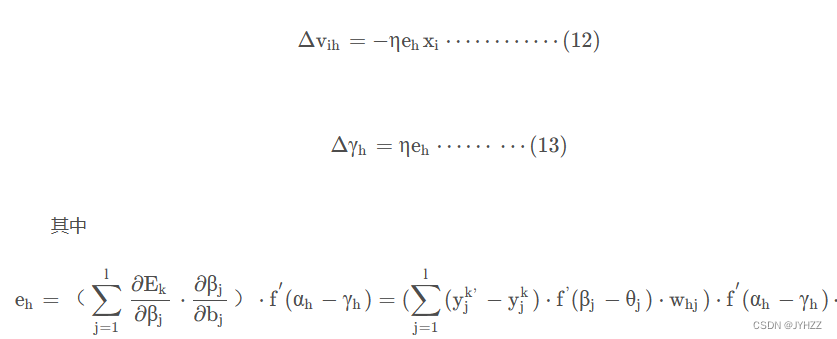
所以推导中w和sitay有共同之处,v和sitah有共同之处。
参考文章:
详解BP神经网络
实现代码:
Iris训练集网上一搜就有
import math
import random
import numpy as np
def readFile(filename, nums, len):
"""
读取iris.txt
iris.txt为150行,每行有5个数据,前4个数据为特征,第五个为所属的类
训练分为全训练和部分训练(打乱顺序)
训练时传入某一行的四个参数,即输入层为4
因为有3类,所以输出层为3,当读入类别时,需要额外做一些处理,不能只读入数值
所以读取数据时全读入,保存到列表中,再根据要求划分出训练集和测试集
流程:
全读入--打乱--按nums划分训练集和测试集--返回
参数
len:文件的行数
nums:范围为(0-1]的数,1 代表全训练,全为测试集,2/3 代表2/3为训练集,1/3为测试集
filename:读取的文件的地址
返回值
train:训练集
test:测试集
"""
train_part = int(len * nums)
test_part = len - train_part
if nums == 1: # 初始化训练集和测试集
train = [[] for i in range(len)]
test = [[] for i in range(len)]
else:
train = [[] for i in range(train_part)]
test = [[] for i in range(test_part)]
f = open(filename, 'r')
filesave = [[] for i in range(len)] # 初始化全集
for i in range(len):
s = f.readline()
s = s.strip('\n')
s = s.strip(' ')
x = s.split('\t')
for j in range(4):
filesave[i].append(eval(x[j]))
if eval(x[-1])==1:
filesave[i].append([1,0,0])
elif eval(x[-1])==2:
filesave[i].append([0,1,0])
else:
filesave[i].append([0,0,1])
numbers = [i for i in range(len)] # 进行打乱处理
random.shuffle(numbers)
if nums == 1:
for i in range(len):
train[i] = filesave[numbers[i]]
test = train[:]
else:
j = 0
for i in range(train_part):
train[i] = filesave[numbers[i]]
for i in range(train_part, len):
test[j] = filesave[numbers[i]]
j += 1
return train, test
def sigmoid(x):
return 1 / (1 + math.exp(-x))
class bp_network:
def __init__(self, train, test, cycles=1200,key=100,node_input=4, node_hide=4, node_output=3):
"""
初始化:
输入层到隐层的权值v 4*4
隐层到输出层的权值w 4*3
隐层的阈值sitah 4
输出层的阈值sitay 3
学习率n
:param train: 训练集
:param test: 测试集
:param cycles: 总训练轮数
:param key: 每隔多少轮测试一次错误率
:param node_input: 输入层结点个数
:param node_hide: 隐层结点个数
:param node_output: 输出层结点个数
"""
self.node_input = node_input
self.node_hide = node_hide
self.node_output = node_output
self.train = train
self.test = test
self.n = 0.01
self.cycles=cycles
self.key=key
self.sitay = [] # 输出层阈值
self.sitah = [] # 隐藏层阈值
self.w = [[] for i in range(node_hide)] # 隐藏层到输出层权值4*3
self.v = [[] for i in range(node_input)] # 输入层到隐藏层权值4*4
#w[h][j] 4*3
for j in range(self.node_output):
self.sitay.append(random.random()) # 输出层阈值
for h in range(self.node_hide):
self.w[h].append(random.random())
#v[i][h] 4*4
for h in range(self.node_hide):
self.sitah.append(random.random()) # 隐藏层阈值
for i in range(self.node_input):
self.v[i].append(random.random())
def bp_predict(self,p):
"""
预测函数,用于测试错误率
思路:遍历测试集,计数错误预测个数
:param p: 第几轮
:return: 无
"""
wrong = 0
for k in range(len(self.test)):
bi = [0 for i in range(self.node_hide)] # 隐层激活后输出
yi = [0 for i in range(self.node_output)] # 输出层输出
for h in range(self.node_hide):
for i in range(self.node_input):
bi[h] += self.v[i][h] * self.test[k][i]
bi[h] = sigmoid(bi[h] - self.sitah[h])
for j in range(self.node_output): # 3
for h in range(self.node_hide): # 4
yi[j] += self.w[h][j] * bi[h]
yi[j] = sigmoid(yi[j] - self.sitay[j])
if test[k][-1][yi.index(max(yi))] ==0:
wrong += 1
print("第",int(p/self.key),"轮正确率:", (1-wrong / len(test)) * 100, "%")
def bp_train(self):
"""
训练函数,用于训练
:return: 无
"""
for p in range(self.cycles):
for k in range(len(self.train)):
bi = [0 for i in range(self.node_hide)] # 隐层激活后输出6
yi = [0 for i in range(self.node_output)] # 输出层输出
gi = []#输出层梯度
eh = []#隐层梯度
# w[h][j] 4*3 v[i][h] 4*4
for h in range(self.node_hide):
for i in range(self.node_input):
bi[h] += self.v[i][h] * self.train[k][i]
bi[h] = sigmoid(bi[h] - self.sitah[h])
for j in range(self.node_output): # 3
for h in range(self.node_hide): # 4
yi[j] += self.w[h][j] * bi[h]
yi[j] = sigmoid(yi[j] - self.sitay[j])
for i in range(self.node_output):
gi.append(yi[i] * (1 - yi[i]) * (train[k][-1][i] - yi[i]))
for h in range(self.node_hide):
temp = 0
for j in range(self.node_output):
temp += self.w[h][j] * gi[j]
eh.append(bi[h] * (1 - bi[h]) * temp)
for h in range(self.node_hide):
for j in range(self.node_output):
self.w[h][j] += self.n * gi[j] * bi[h]
for j in range(self.node_output):
self.sitay[j] += -self.n * gi[j]
for h in range(self.node_hide):
for i in range(self.node_input):
self.v[i][h] += self.n * eh[h] * train[k][i]
for h in range(self.node_hide):
self.sitah[h] += -self.n * eh[h]
if p % self.key == 0:
self.bp_predict(p)
if __name__ == "__main__":
train, test = readFile("D:\\PythonProject_Class\\test_Data\\iris.txt", 2/3, 150)
bp = bp_network(train, test,node_hide=5,cycles=2400)
bp.bp_train()