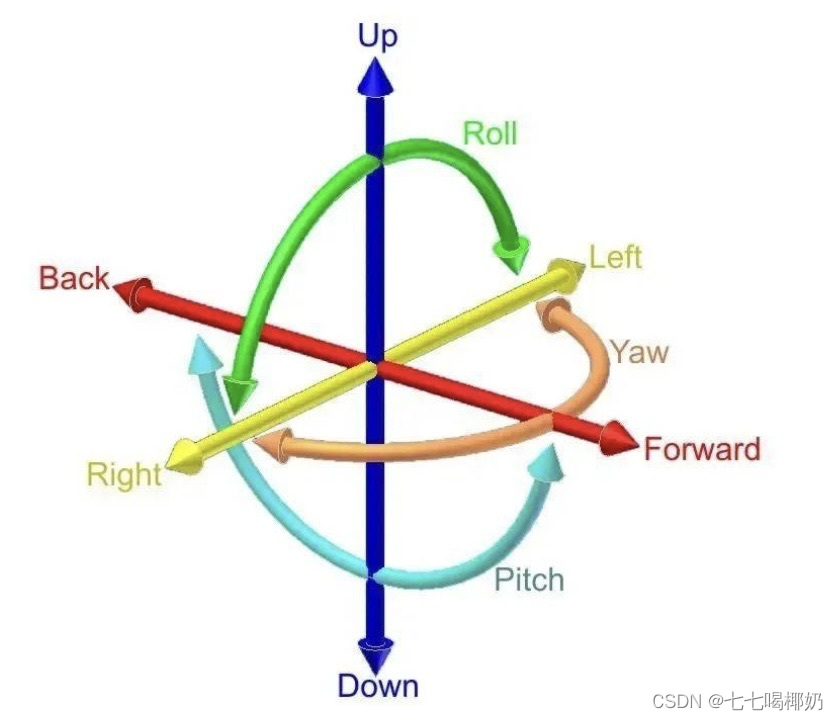
坐标系定义
- 1. 图像坐标系
- 2. 摄像机坐标系
- 3. 世界坐标系
- 4. 三种坐标系间的转换
- 4.1 摄像机坐标系与无畸变图像坐标系之间的变换
- 4.2 世界坐标系与摄像机坐标系之间的变换
- 4.3 世界坐标系与无畸变图像坐标系之间的变换
1. 图像坐标系

数字图像坐标系:
O
0
−
u
v
O_0-uv
O0−uv,每一像素
(
u
,
v
)
(u,v)
(u,v)是该像素在图像数组中的列数和行数
物理图像坐标系:
O
−
x
y
O-xy
O−xy,每一像平面坐标
(
x
,
y
)
(x,y)
(x,y)是真实的物理尺寸
若每个像素在
x
x
x轴和
y
y
y轴方向的物理尺寸为
d
x
d_{x}
dx、
d
x
d_{x}
dx ,则任意像素在两坐标系下关系:
[
u
v
1
]
=
[
1
d
x
0
u
0
0
1
d
y
v
0
0
0
1
]
[
x
y
1
]
\begin{bmatrix}u\\ v\\ 1\end{bmatrix}=\begin{bmatrix}\frac{1}{d_x}&0&u_0\\ 0&\frac{1}{d_y}&v_0\\ 0&0&1\\ \end{bmatrix}\begin{bmatrix}x\\ y\\ 1\end{bmatrix}
uv1
=
dx1000dy10u0v01
xy1
2. 摄像机坐标系
摄像机坐标系(相机坐标系) O c − X c Y c Z c O_c-X_cY_cZ_c Oc−XcYcZc:由摄像机光心 O c O_c Oc、轴 X c X_c Xc、轴 Y c Y_c Yc、光轴 Z c Z_c Zc 组成的直角坐标系称为摄像机坐标系。
3. 世界坐标系
世界坐标系(全局坐标系)
O
w
−
X
w
Y
w
Z
w
O_w-X_wY_wZ_w
Ow−XwYwZw:为了选择一个基准坐标系来描述摄像机的位置,并用它描述环境中任何物体的位置,由
O
w
O_w
Ow、轴
X
w
X_w
Xw、轴
Y
w
Y_w
Yw 、轴
Z
w
Z_w
Zw 组成。
摄像机坐标系与世界坐标系的关系如下图所示:

4. 三种坐标系间的转换
4.1 摄像机坐标系与无畸变图像坐标系之间的变换
用 ( f x , f y ) (f_x,f_y) (fx,fy)表示摄像机焦距,即三维空间中的一点经摄像机成像后,所投影到图像平面上的坐标在 X ,Y 方向上的缩放比例不一样。由小孔成像原理得透视投影变换为如下形式: [ u i v i 1 ] = [ f x d x z c 0 u 0 0 0 f y d y z c v 0 0 0 0 1 z c 0 ] [ x c v c v c 1 ] = M 1 x ~ c \begin{bmatrix}u_i\\v_i\\1\end{bmatrix}=\begin{bmatrix}\frac{f_x}{d_xz_c}&0&u_0&0\\0&\frac{f_y}{d_yz_c}&v_0&0\\0&0&\frac{1}{z_c}&0\end{bmatrix}\begin{bmatrix}x_c\\v_c\\v_c\\1\end{bmatrix}=M_1\tilde{x}_c uivi1 = dxzcfx000dyzcfy0u0v0zc1000 xcvcvc1 =M1x~c
4.2 世界坐标系与摄像机坐标系之间的变换
x ~ c = [ x c y c z c 1 ] = [ R p 0 τ 1 ] [ x w y w z w 1 ] = M 2 x ~ w x ~ w = M 2 − 1 x ~ c \begin{gathered} {\tilde{x}}_{c} ={\left[\begin{array}{l}{x_{c}}\\ {y_{c}}\\ {z_{c}}\\ {1}\end{array}\right]}={\left[\begin{array}{l l}{R}&{\boldsymbol{p}}\\ {\boldsymbol{0}}^{\tau}&{1}\end{array}\right]}{\left[\begin{array}{l}{x_{w}}\\ {y_{w}}\\ {z_{w}}\\ {1}\end{array}\right]}=M_{2}{\tilde{x}}_{w} \\ {\tilde{x}}_{_w}={M_{2}}^{-1}{\tilde{x}}_{c} \end{gathered} x~c= xcyczc1 =[R0τp1] xwywzw1 =M2x~wx~w=M2−1x~c
4.3 世界坐标系与无畸变图像坐标系之间的变换
[ u i v i 1 ] = [ f x d x z c 0 u 0 0 0 f y d y z c v 0 0 0 0 1 z c 0 ] [ R p 0 T 1 ] [ x w y w z w 1 ] = M 1 M 2 x ~ w = M x ~ w \begin{bmatrix}u_i\\v_i\\1\end{bmatrix}=\begin{bmatrix}\frac{f_x}{d_xz_c}&0&u_0&0\\0&\frac{f_y}{d_yz_c}&v_0&0\\0&0&\frac{1}{z_c}&0\end{bmatrix}\begin{bmatrix}R&\boldsymbol{p}\\\boldsymbol{0}^T&1\end{bmatrix}\left[\begin{array}{c}x_w\\ y_w\\ z_w\\ 1\end{array}\right]=M_1M_2\tilde{x}_w=M\tilde{x}_w uivi1 = dxzcfx000dyzcfy0u0v0zc1000 [R0Tp1] xwywzw1 =M1M2x~w=Mx~w
M 1 M_1 M1为内参, M 2 M_2 M2为外参, M M M为投影矩阵,表征二维图像坐标与三维世界坐标间的基本关系。