图基本概念
点相同 边相同 $$

有向图 无向图
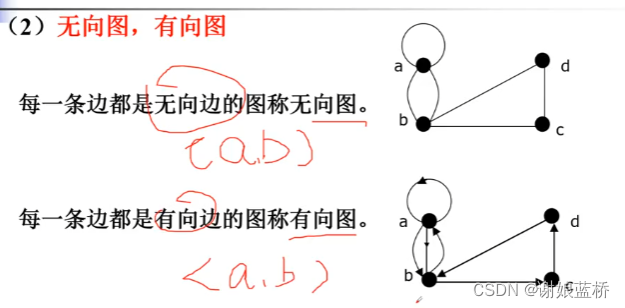

邻接点 :两个结点有一条有(无)向边相关联
邻接边:关联与同一个结点
孤立结点: 不予任何结点相邻接的结点



握手定理 度数=边的两倍


有向图的 出度和=入度和=边数







n个节点无向完全图边数 C n 2 = 1 2 n ( n − 1 ) C_n^2 = \frac 1 2 n(n-1) Cn2=21n(n−1)

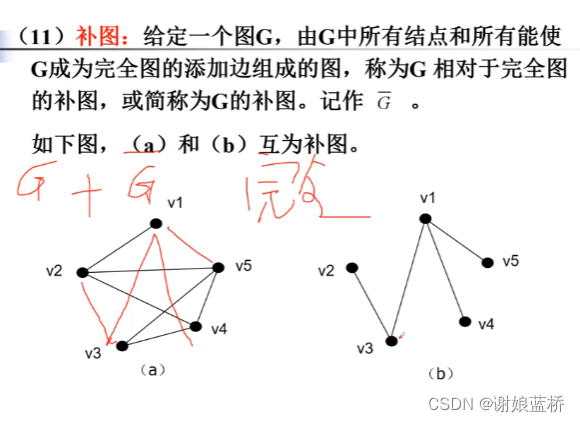


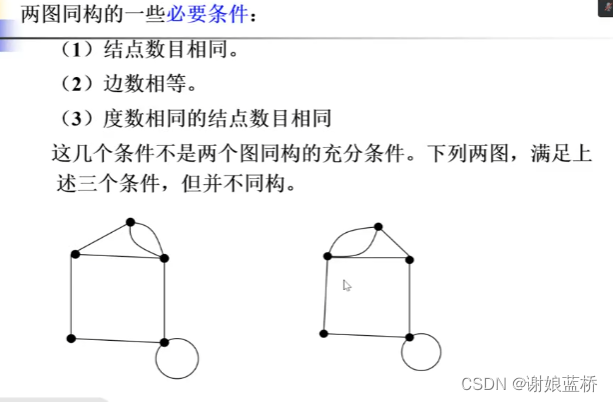
图同构
必要条件 节点数相同 边相同 度数相同节点数目相同

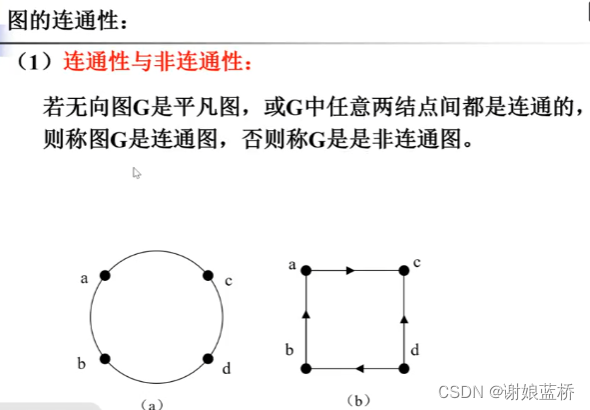
连通性



任意两个节点都是相连的




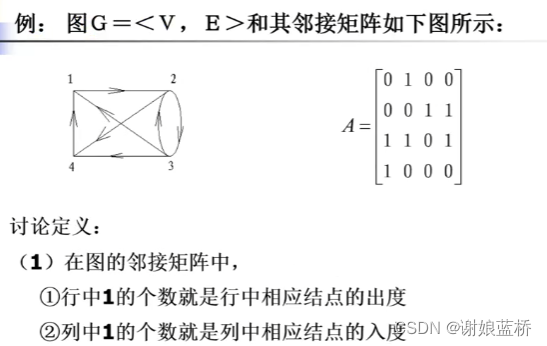

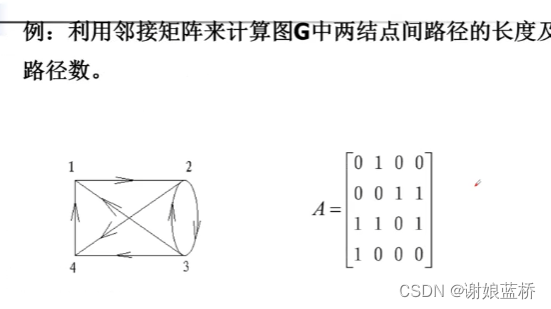








特殊图
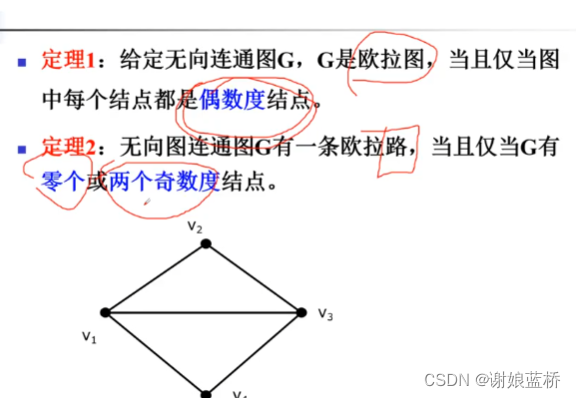
欧拉环路(欧拉) 欧拉路中每个节点都是偶数度节点





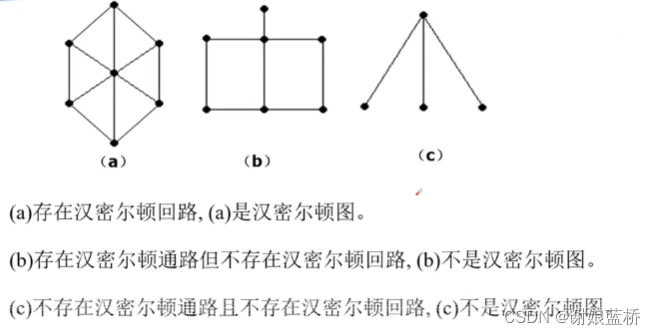
汉密尔顿与回路






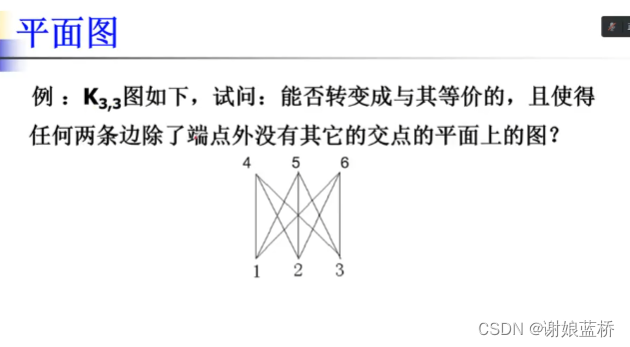
平面图


一条边被两个面公用 面数次数之和等于边的2倍

欧拉公式 n个结点 m条边 面数r : n-m +r =2








m
=
C
n
2
=
5
∗
4
/
2
=
10
m=C_n^2=5*4/2=10
m=Cn2=5∗4/2=10
n
=
5
n=5
n=5
由推论 m
≤
3
n
−
6
\le3n-6
≤3n−6 得 m
≤
9
\le9
≤9 相互矛盾
对偶图

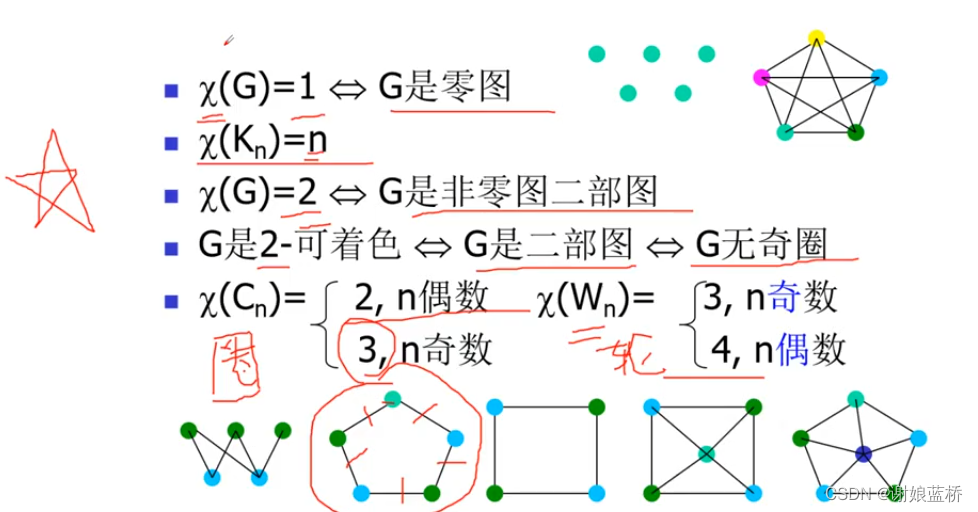
二部图 图形的着色


点着色


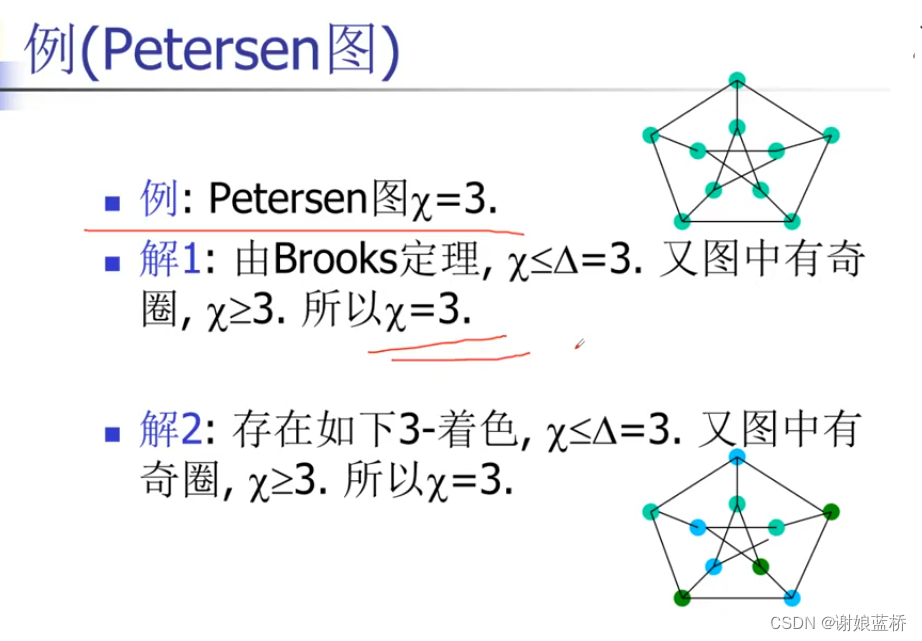
树
∑
d
e
g
(
v
i
)
=
2
e
=
2
V
−
2
\sum deg(v_i)=2e =2V -2
∑deg(vi)=2e=2V−2
所有点的度数和等于结点数减1再乘以2
e
=
V
−
1
e = V -1
e=V−1
边数等于结点数减一 (除去根结点)