前言
哈希冲突是无法避免的,只能尽可能的减少冲突的可能性,通常我们可以设计适合的哈希函数。但是,哈希冲突还是会发生,那我们如何解决呢?
我们可以使用闭散列/开放定址法的方法,解决哈希冲突

文章目录
- 前言
- 一. 闭散列
- (1). 线性探测
- (2). 二次探测
- 二. 闭散列的实现
- (1). 结构
- (2). 插入
- (3). 查找
- (4). 删除
- (5). 测试
- 三. 完整代码
- 结束语
一. 闭散列
闭散列:又叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明哈希表中还有空位置,那么可以把冲突的元素放到冲突位置的 “ 下一个 ” 空位
“ 下一个 ” 空位的寻找,有以下几种常用方法:
(1). 线性探测
比如这样一个数组:{1 , 77 , 6 , 14 , 5 , 9}
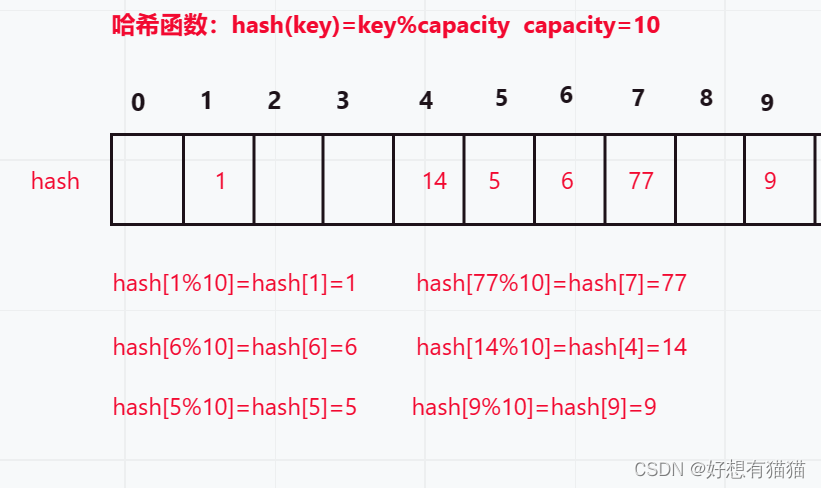
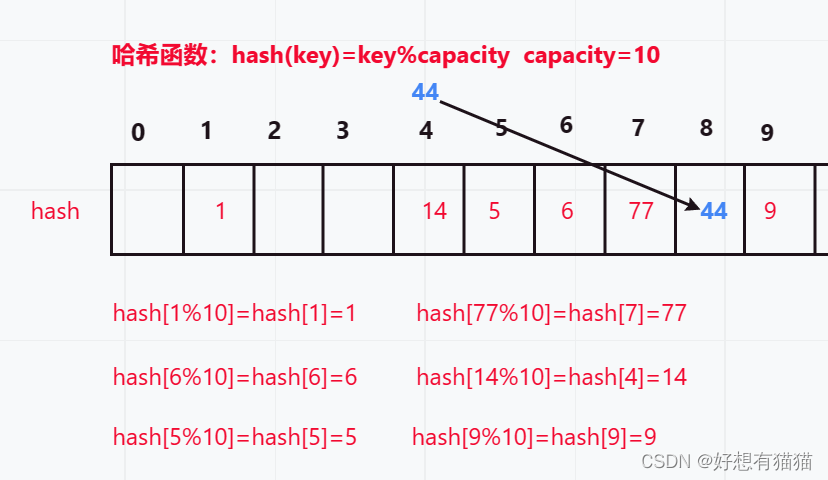
初次的映射没有产生哈希冲突,但是当我们再插入一个44时,哈希冲突就产生了。
而线性探测:从发生冲突的位置,依次向后探测,直到寻找到下一个空位置为止
插入:
- 通过
哈希函数获取待插入元素在哈希表中的位置 - 如果该位置没有元素则直接插入新元素,如果该位置中有元素,发生
哈希冲突,那么使用线性探测,找到下一个空位,插入新元素
删除:
我们不可以采用覆盖的方法,因为任何值都可以是插入的值,无法分辨该值是插入还是删除,所以我们可以采用状态标记的方法,标记一个值的删除
(2). 二次探测
线性探测的缺陷是,产生冲突的数据堆积在一起,则线性探测的次数会变得很多。
而二次探测是将每次向后探测的位置由1,2,3,4这样的线性变化,变成1,4,9,16,这样的非线性变化,使得每次产生哈希冲突后,下一个空位分部散乱,再冲突的可能性降低
二. 闭散列的实现
接下来,我们使用代码将其实现
我们采用线性探测的方式,和除留余数法的哈希函数
(1). 结构
首先,我们可以使用一个枚举定义哈希表结点的状态:1.存在值 2. 删除值 3. 空
结点存储的是键值对
闭散列中,使用一个vector,存储哈希表结点,并有一个记录当前存储个数的成员变量
代码如下:
//状态标记位
enum State
{
EMPTY,//空
EXIST,//存在
DELETE//删除
};
//哈希结点
template<class K,class V>
struct HashNode
{
pair<K, V>_kv;//键值对
State _state = EMPTY;//状态标记位
};
//闭散列
//哈希表
template<class K,class V>
class HashTable
{
typedef HashNode<K, V> Node;
private:
vector<Node> _tables;//线性表
size_t _n = 0;//大小
};
(2). 插入
根据上述所讲述的步骤
插入:
- 通过
哈希函数获取待插入元素在哈希表中的位置 - 如果该位置没有元素则直接插入新元素,如果该位置中有元素,发生
哈希冲突,那么使用线性探测,找到下一个空位,插入新元素
//插入
bool Insert(const pair<K,V>kv)
{
//1. 映射位置
size_t hashi = kv.first % _tables.size();
size_t indix = hashi;
size_t i = 1;//线性探索的距离
//2.线性探索
while (_tables[indix]._state == EXIST)
{
indix = hashi + i;
indix %= _tables.size();
i++;
}
_tables[indix]._kv = kv;
_tables[indix]._state = EXIST;
_n++;
return true;
}
但是,这份代码还存在诸多问题
- 最开始哈希表的大小为0,那么就会出现除零异常
- 如果哈希表的容量满了,那么是否需要扩容
我们解决了扩容的问题,最开始容器为空时就会自动扩容,除零异常自然就解决了。
STL中,vector的扩容,是重新申请更大的空间,然后将原本空间的数据拷贝到新空间
但是哈希表的扩容不能如此,因为我们采用的是除留余数法,当容量发生改变后,不同关键字根据哈希函数得出的哈希地址就不同
还是这个图

当前容量为10,所以14的哈希地址是4,但是如果容量扩大到了20,那么14的哈希地址就变成14了。所以每一次扩容,原先的映射关系就会发生改变,不能直接拷贝
同时,我们可以控制负载因子,来决定什么时候扩容
负载因子/载荷因子
负载因子α = 当前插入元素个数 / 容量
由于表长是定址,α与 “ 填入表中的元素个数 ”成正比,所以,α越大,表面填入表中的元素越多,产生冲突的可能性就越大;反之,α越小,表面填入表中的元素越少,产生冲突的可能性就越小。实际上,散列表的平均查找长度是负载因子的函数,只是不同处理冲突的方法有不同的函数
对于开放定址法,负载因子是特别重要的因素,严格限制在0.7~0.8以下,超过0.8,查表时的CPU缓存不命中,按照指数曲线上升。因此,超过时需要即使扩容
扩容,我们可以直接重新建立一个哈希表,然后调用遍历原先容器,将值重新映射新的哈希表中,最后交换一下新旧表的vector,就完成了扩容
代码如下:
//插入
bool Insert(const pair<K,V>kv)
{
//判断是否需要扩容
//当前大小为0 || 负载因子超过0.7
if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7)
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
HashTable<K, V>newTable;
//重新构造一个HashTable完成映射
newTable._tables.resize(newSize);
//重新映射
for (auto &data : _tables)
{
if (data._state == EXIST)
{
newTable.Insert(data._kv);
}
}
//交换新旧表的vector
_tables.swap(newTable._tables);
}
//插入新元素
//映射位置
size_t hashi = kv.first % _tables.size();
size_t indix = hashi;
//线性探索的距离
size_t i = 1;
//线性探索
while (_tables[indix]._state == EXIST)
{
indix = hashi + i;
indix %= _tables.size();
i++;
}
_tables[indix]._kv = kv;
_tables[indix]._state = EXIST;
_n++;
return true;
}
(3). 查找
哈希表最高效的就是查找
而查找的逻辑,其实依照根据哈希函数实现的。
首先,我们先查看,查找的值经过哈希函数产生的哈希地址,是否直接就存储着该元素,如果是,那么直接返回
如果不是,那么根据线性探测,依次向后查找,直到查找到空,代表当前哈希表没有该元素
代码如下:
//查找
Node* Find(const K&key)
{
//空表直接返回空指针
//保证不会出现除0异常
if (_tables.size() == 0)
return nullptr;
//根据哈希函数求得哈希地址
size_t hashi = key % _tables.size();
size_t indix = hashi;
size_t i = 1;
//直到查找到空为止
while (_tables[indix]._state!=EMPTY)
{
//可能查找的是已经删除的数据
if (_tables[indix]._state == EXIST &&
_tables[indix]._kv.first == key)
{
return &_tables[indix];
}
indix = hashi + i;
indix %= _tables.size();
++i;
//可能出现全是删除和存在的情况
if (hashi == indix)
{
//说明已经查了一圈了
return false;
}
}
//到这就是没找到
return nullptr;
}
需要注意的是
- 可能出现当前为
空表,但还是查找的情况,这会出现除零异常,我们单独判断一下 - 线性探测的过程中,如果一个元素是删除的,我们只会将其状态标志位改为
DELETE,其值还存在,所以我们查找的到元素需要是EXIST的,才算是查找成功 - 可能出现当前表删除一些元素,再插入一些元素,负载因子并未超过0.7,但是插入的元素刚好将所有EMPTY的位置都占满,导致哈希表只有DELETE和EXIST的情况,这时会导致死循环,所以当indix==hashi时,代表
已经查找完一整圈了,就直接返回,没有找到
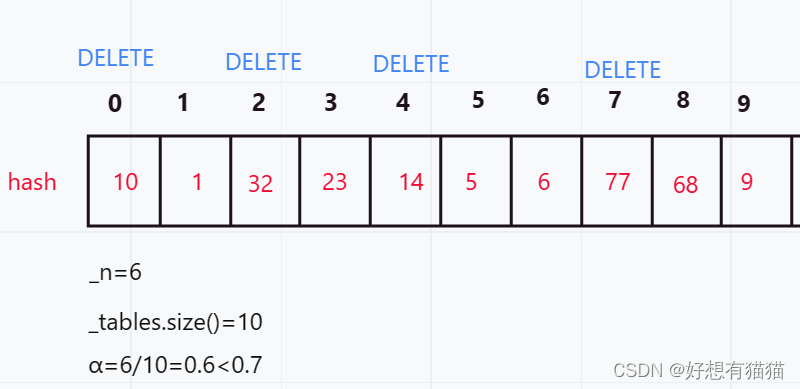
如图,此时哈希表中只有DELETE和EXIST,没有EMPTY。
我们还可以在插入中,复用查找

如果返回的是,不是空指针,说明该值在哈希表中存在,直接返回假
(4). 删除
删除的逻辑,只要将其标志位改为DELETE就好
代码如下:
//删除
bool Erase(const K&key)
{
Node*ret = Find(key);
if (ret)
{
ret->_state = DELETE;
_n--;
}
else
{
return false;
}
return true;
}
(5). 测试
我们编写一个遍历的算法
只访问标记位为EXIST的元素
//遍历
void traverse()
{
if (_tables.size() == 0)
{
cout << "当前表为空" << endl;
return;
}
for (int i = 0; i < _tables.size(); i++)
{
if (_tables[i]._state == EXIST)
{
cout << _tables[i]._kv.first << " : " << _tables[i]._kv.second << endl;
}
}
}
测试如下:
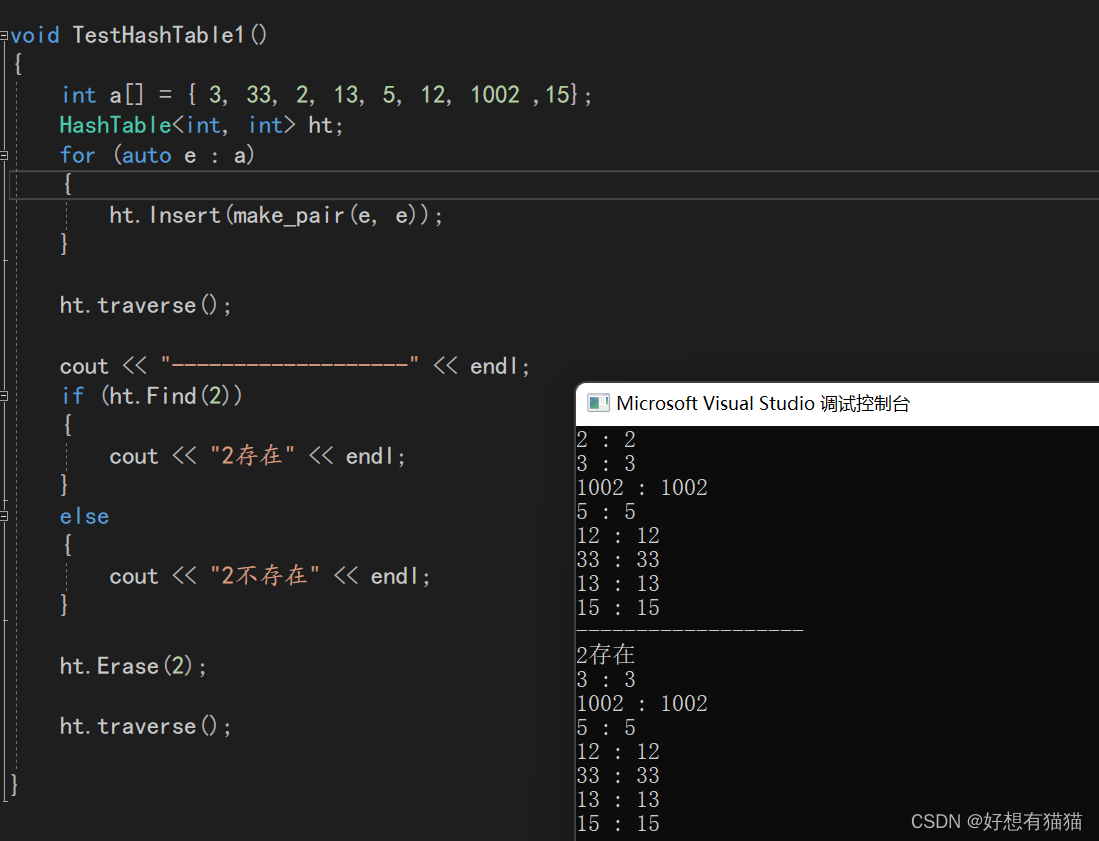
void TestHashTable1()
{
int a[] = { 3, 33, 2, 13, 5, 12, 1002 ,15};
HashTable<int, int> ht;
for (auto e : a)
{
ht.Insert(make_pair(e, e));
}
ht.traverse();
cout << "-------------------" << endl;
if (ht.Find(2))
{
cout << "2存在" << endl;
}
else
{
cout << "2不存在" << endl;
}
ht.Erase(2);
ht.traverse();
}
运行结果如下:
三. 完整代码
头文件请在.cpp中自行包含
#pragma once
//状态标记位
enum State
{
EMPTY,//空
EXIST,//存在
DELETE//删除
};
//哈希结点
template<class K,class V>
struct HashNode
{
pair<K, V>_kv;
State _state = EMPTY;
};
//哈希表
template<class K,class V>
class HashTable
{
typedef HashNode<K, V> Node;
public:
//插入
bool Insert(const pair<K,V>kv)
{
//可以复用查找看一下当前值是否已经存在
if (Find(kv.first))
return false;
//判断是否需要扩容
//当前大小为0 || 负载因子超过0.7
if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7)
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
HashTable<K, V>newTable;
//重新构造一个HashTable完成映射
newTable._tables.resize(newSize);
//重新映射
for (auto &data : _tables)
{
if (data._state == EXIST)
{
newTable.Insert(data._kv);
}
}
_tables.swap(newTable._tables);
}
//映射位置
size_t hashi = kv.first % _tables.size();
size_t indix = hashi;
//线性探索的距离
size_t i = 1;
//线性探索
while (_tables[indix]._state == EXIST)
{
indix = hashi + i;
indix %= _tables.size();
i++;
}
_tables[indix]._kv = kv;
_tables[indix]._state = EXIST;
_n++;
return true;
}
//查找
Node* Find(const K&key)
{
//空表直接返回空指针
//保证不会出现除0异常
if (_tables.size() == 0)
return nullptr;
//根据哈希函数求得哈希地址
size_t hashi = key % _tables.size();
size_t indix = hashi;
size_t i = 1;
//直到查找到空为止
while (_tables[indix]._state!=EMPTY)
{
//可能查找的是已经删除的数据
if (_tables[indix]._state == EXIST && _tables[indix]._kv.first == key)
{
return &_tables[indix];
}
indix = hashi + i;
indix %= _tables.size();
++i;
//可能出现全是删除和存在的情况
if (hashi == indix)
{
//说明已经查了一圈了
return false;
}
}
//到这就是没找到
return nullptr;
}
//删除
bool Erase(const K&key)
{
Node*ret = Find(key);
if (ret)
{
ret->_state = DELETE;
_n--;
}
else
{
return false;
}
return true;
}
//遍历
void traverse()
{
if (_tables.size() == 0)
{
cout << "当前表为空" << endl;
return;
}
for (int i = 0; i < _tables.size(); i++)
{
if (_tables[i]._state == EXIST)
{
cout << _tables[i]._kv.first << " : " << _tables[i]._kv.second << endl;
}
}
}
private:
vector<Node> _tables;//线性表
size_t _n = 0;//大小
};
结束语
本篇内容到此就结束了,感谢你的阅读!
如果有补充或者纠正的地方,欢迎评论区补充,纠错。如果觉得本篇文章对你有所帮助的话,不妨点个赞支持一下博主,拜托啦,这对我真的很重要。