当我们在做Kmeans聚类的准备工作时,通常会用到手肘法(elbow method)或者轮廓系数(silhouette score)去找到最佳簇类个数。
对于轮廓系数寻找法,理论上来说,轮廓系数会随着聚类个数的增加而增加,再而减少,直到我们找到最大的轮廓系数对应的簇类个数。如下图。
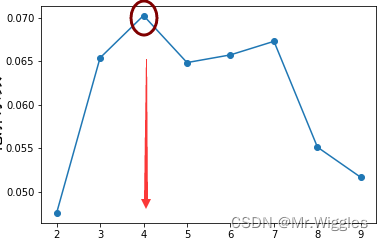
但实际在某些情况下,会出先减少后增加再减少的“过山车”or“凸点”情况,这其中是由于数据的特性和聚类算法的性质所导致的。
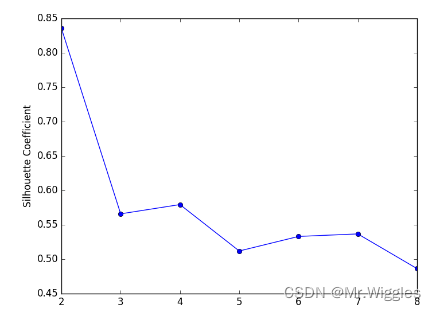
参考轮廓系数的公式
S
(
i
)
=
b
i
−
a
i
m
a
x
(
a
i
,
b
i
)
S(i)=\frac{b_i-a_i}{max(a_i,b_i)}
S(i)=max(ai,bi)bi−ai
- a i a_i ai:即样本点i到所属簇类点的平均距离,表示为凝聚度
- b i b_i bi:即样本点i到非所属簇类点的平均距离,表示为分离度
当出现轮廓系数在初始阶段比较大情况时,有可能此时 b i b_i bi远远大于 a i a_i ai,分离度较高,导致 a i a_i ai在增加过程中远不及 b i b_i bi分离度带来的影响大,而当簇类个数增加时,会使得 b i b_i bi逐渐减小,此时轮廓系数会变小。当簇类之间的距离区域稳定后,才会慢慢的呈现轮廓系数先升高后降低的趋势。此时的轮廓系数最高点对应的簇类个数可能才作为我们的最佳聚类个数。
话说回来,“过山车”情况是由于数据的特性和聚类算法的性质所导致的,所以我们的在找最佳聚类个数时,可以通过改变Kmeans算法的种子数seed,使得初始化不同簇类中心点的位置不会离得这么远,这样才能做到轮廓系数先增加后减少的趋势。