深度学习用于医学预后-第二课第三周8-13节-估计生存函数

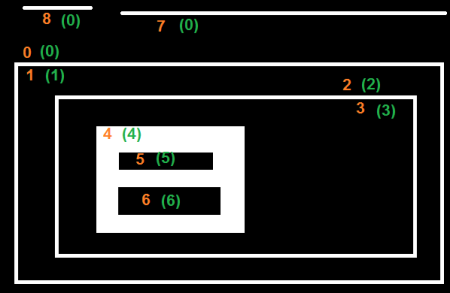
上节课知道了数据中存在删失数据，那么我们如何利用这些数据建立生存函数。这将是本节课的重点内容。

文章目录

- 估计生存函数
- 立即死亡还是永远存活
- 生存概率介于两者之间
- 使用删失数据
- 条件概率的链式法则
- 推导生存函数
- 根据数据计算概率

估计生存函数

本节课，我们将学习估计生存函数。回想一下我们看过的病人生存模型。对于这些病人，生存模型会告诉我们生存函数，也就是S(t)，可以用上图来表示，在每个时间点，我们可以知道生存概率是多少。

生存概率，记住，就是某个事件发生的时间在某个小t之后的概率，这个小t可以是1年，可以是5年，可以是10年，无论我们关心的是什么时间。

我们研究了生存数据，对于生存数据我们有一组病人我们以时间的形式收集了结果信息。我们将使用这种形式的信息来估计生存函数。

注意：我们现在还没有为每个病人建立个性化的生存函数，我们以后再看怎么做。但现在，对于人群中的任何人，我们将应用相同的生存曲线，也就是说，对于每个t，我的生存概率是多少?我们可以从上述图中看出，这是一个适用于整体的生存函数而不是个人。

立即死亡还是永远存活

我们将尝试对存活到t个月的概率进行建模。对于我们的例子，让t等于25个月。我们可以从数据中估计这一点。方法是，存活到25个月的数量除以数据中的患者总数。

让我们来看一下在 25 个月时存活的数量。我们知道三号患者存活到了 25 个月，六号患者也是如此，因为他们的事件发生时间大于 25 个月。不幸的是，让这个估计变得复杂的事情是我们有这些右删失的观测数据。

请记住，右删失观测数据的问题在于我们不知道事件何时发生；如果它们有事件发生，我们对事件发生的时间有一个下限。因此我们必须在这里做出一个假设，让我们尝试一下两种假设。

第一种假设是他们立即死亡。例如，二号患者在 8 个月被删失，那么我们就假设这个个体在我们接触后立即死亡。这种情况下，在 25 个月时存活的人数只包括三号和六号患者，分母是所有患者，即 7。这个估计结果约为 0.29。
第二个假设是，每一个被删失观测到的个体永远不会死亡。也就是说，二号、五号和七号患者将一直活着，肯定会超过 25 个月。这样我们就有了另外三个在 25 个月后存活的患者，加上最初的两个患者。因此我们更新后的估计结果为5/7，这样的生存概率约为 0.71。

请注意，如果我们假设这些被删失观测数据中的所有个体都立即死亡，那么生存概率要比我们假设它们从未死亡的时候小得多。现在我们知道事实上的情况应该在这两个值之间。

生存概率介于两者之间

假设我们能够联系到这些患者，我们可以找出这些右删失观测数据的真实值。我们打了一些电话，然后得到了这些患者的真实信息

其中两个患者的时间大于 25 个月，另一个则小于 25 个月。我们可以基于这些真实信息重新估计我们在 25 个月时的生存率。这将包括存活至 25 个月的患者人数，即二号、三号、五号和六号患者。生存概率=4/7。

请注意，在假设每个被删失观测到的个体立即死亡或他们永远不会死亡的情况下，我们之前得到的结果分别是 2/7 和 5/7。而现实似乎处于这两个数字中间，即三个患者中有两个在 25 个月后存活，而另一个没有。

这个问题并不总是出现，我们很遗憾并不总能获取到右删失观测数据的真实情况。

因此，在处理生存模型时我们需要回答一个非常重要的问题：当我们有右删失观测资料又不方便联络个体获取真实发生事件的时间时，我们如何估计在某个时间 t（这里是 25 个月）之后的存活概率？下面我们将探讨更多相关的内容。

使用删失数据

我们将用右删失数据估计在 25 个月后的存活概率。因此，我们会从一个数轴开始，数轴上标记着从零到 25 及其之后的时间点。

请注意，我们只考虑离散的时间点，因为事件要么发生在一个时间点，要么发生在下一个时间点，而不会在两个时间点之间发生。

然后估计在 25 个月后的存活概率。我们有 S(25)，即时间到达事件发生时间在 25 个月之后的概率。请注意，如果一个事件在 25 个月之后发生，那么它在 26 个月之后或刚好在 26 个月时才会发生。

因此，我们需要进行一些修正，并将其写成时间到达事件发生时间在 26 个月之后或刚好在 26 个月时的概率形式。我们将逐步扩展这个概率式子。时间到达事件发生时间在 26 个月之后或刚好在 26 个月时这个条件所表达的含义是：时间到达事件发生时间在 26 个月之后且在 25 个月之后、在 24 个月之后以及所有之前的月份，或者是刚刚在 26 个月或刚好在 25、24 等所有之前的时间点时。

我们可以这样做，是因为条件一意味着条件二的成立。

条件概率的链式法则

什么是链式法则？

条件概率的链式法则是计算多个事件同时发生的条件概率的方法，它可以用以下公式表示：

$P (A 1 \cap A 2 \cap ... \cap A n) = P (A 1) * P (A 2∣ A 1) * P (A 3∣ A 1 \cap A 2) * ... * P (A n ∣ A 1 \cap A 2 \cap ... \cap A n - 1)$

其中， $P (A i ∣ B)$ 表示在事件 B 发生的条件下事件 Ai 发生的概率。整个公式意味着：要计算 n 个事件 $A 1, A 2, ..., A n$ 同时发生的概率，需要从第一个事件开始，计算每个事件在前面事件已经同时发生的条件下发生的概率，逐一乘起来即可。

例如，假设有三个事件 A, B 和 C，在 A 发生的条件下计算 B 的概率，再在 A 和 B 都发生的条件下计算 C 的概率，则它们同时发生的条件概率为：

$P (A \cap B \cap C) = P (A) * P (B ∣ A) * P (C ∣ A \cap B)$

这个公式先计算 A 发生的概率，然后根据 A 发生的条件下计算 B 发生的概率，最后根据 A 和 B 发生的条件下计算 C 发生的概率。通过这种方式，我们可以将计算多个事件的联合概率问题分解成一系列条件概率问题，并且逐步考虑每个事件发生的可能性。

所以我们的S（25）是T大于等于26，大于等于25的概率，依此类推，直到零。我们之所以把它发展到这个阶段，是因为现在我们可以使用条件概率的链式规则来进一步分解它。

因此，我们可以使用条件概率的链式规则，如上图所示，T大于等于0的概率恒等于1。不需要在乘法中包含这个项，因此可以划掉。

推导生存函数

所以我们用以上表达式表示了生存概率，即生存到25岁的概率是一系列概率的乘积。这些概率表示了如果我活到了25岁，我会活到26岁的概率是多少？将其乘以在我到达24岁后我能活到25岁的概率，以此类推，直到我们回到时间开始的地方，并询问问题，如果我们活过0岁，那么我们活到1岁的可能性是多少？所以我们在这个时间轴上做了这些小小的步骤，来计算我们关心的生存概率，也就是25岁。我们将通过理解这种计算方法如何更细分来对这个公式进行进一步修改。

公式中第一项 $P r (T >= 26∣ T >= 25)$ 表示已经在 25 或之后发生了此事件。它等于 $P r (T > 25∣ T >=; 25)$ , 进一步等于 $1 - P r (T = 25∣ T >= 25)$

所以 S(25) 将会是1减去事件恰好在 25 个月时发生的概率，假设它在 25 个月或之
后发生，这是第一个术语。第二项将是 1 减去在 24 个月及之后发生时，该事件在 24 个月时发生的概率等等，直到我们到达最后一项，即事件在 0 个月时发生的概率在它在 0 个月之后发生的情况下的补集概率。

接下来，我们将看到为什么用以下方式表示生存概率是有用的。

根据数据计算概率

因此，我们已经看到了如何使用以上表达式表示生存函数，使用这种表达式的好处是我们可以直接从数据中估计该数量。

因此，在给定时间内事件发生的概率可以通过查看在该时间死亡的患者数量来进行估计。例如，公式第一项，分母等于活过25月的患者数量，分子等于刚好25月去世的患者数量。这些数据都可以从数据中表中获取。

由于我们看到没有患者恰好在25岁时去世，因此我们的分子为0。现在在分母中，我们正在寻找已知存活至25月的患者人数。所以浏览这些患者，患者3存活至25岁，而患者6已知存活至25岁，因此此处的分母为2。
因此， $1 - P r (T = 25∣ T >= 25) = 1 - 0 = 1$
事实上，我们仅会看到两个患者在25岁之前死亡，这将是在时间为10时的患者1和在时间为20时的患者4。因此，该表达式简化为在这两个时间点计算此表达式

我们已经看到了如何简化此表达式，使其具有这两个术语，请看看我们如何进一步简化它。

从图上，我们最终计算出 $s (25) = 0.56$