高斯牛顿法详解_我只是一只自动小青蛙的博客-CSDN博客
一、思想
先看一下牛顿高斯迭代法的缺点:
1、在计算的过程中可能会出现奇异矩阵(不满秩),比如:J(k))TJ(k) 为病态矩阵的时候就不能得到正确的解,或者在求inv((J(k))TJ(k) )的时候不可逆,那么这个就无法在计算下去了
2、当Δxk的过大的时候可能会导致,x(k+1)=x(k)+Δxk 迭代不准确,算法不收敛
因此:在这个基础上提出了置信区间u

对于病态矩阵,L-M提出了采用系数矩阵阻尼的方法来改造矩阵J(k))TJ(k)使得算法能计算下去。
二、步骤
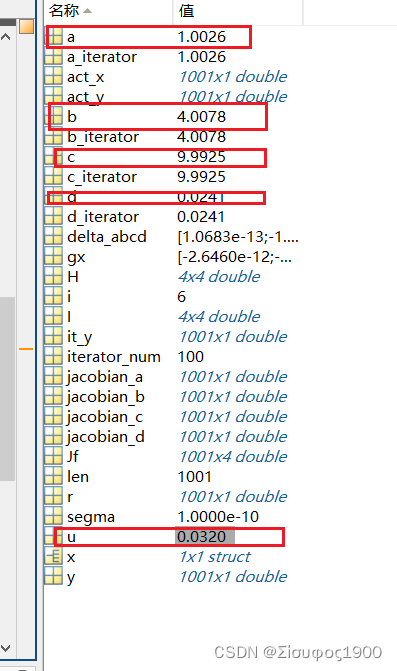
1、初始值设定 u 和系数初始值 a b c d
2、计算(Jf'*Jf +uI)delta_x=Jf'f(x) ,解出delta_x,
3、判断精度
4、xk=xk+delta_x
5、判断p 并迭代出新的u
p>0.75 u=2u
p<0.25 u=0.5u
当ρ接近1时,近似效果好;
当ρ 太小时,实际减小的值远小于近似函数减小的值,近似效果差,需要缩小近似范围μ
当ρ较大时,实际减小的值大于近似函数减小的值,近似效果差,需要增大近似范围μ
% L-M 迭代算法
close all;
clear ;
clc;
% y(i)=a*exp(-(x(i)-b).^2/c.^2)+0.1*rand(1); 函数模型
% 在拟合数据的时候用的系数是
% a=1;
% b=4;
% c=10;
% 因此在拟合参数的时候,这里用 a=0.866
a=0.966;
b=3.98;
c=9.98;
d=0;
% 设置优化半斤
u=0.001;
segma=0.0000000001;% 精度
iterator_num=100;% 最大跌代次数
x=load('x.mat');
act_x=x.x;
y=load('y.mat');
len=length(act_x);
jacobian_d=ones(len,1);
I=ones(4,4);
act_y=y.y;
plot(act_x,act_y,'.');
hold on;
for i=1:iterator_num
% 计算误差
y=a*exp(-(act_x-b).^2/c.^2)+d;
r=act_y-y;
% 开始计算偏导数矩阵
jacobian_a=exp(-(act_x - b).^2/c.^2);
jacobian_b=(a*exp(-(act_x - b).^2/c.^2).*(2.*act_x - 2*b))/c.^2;
jacobian_c=(2*a*exp(-(act_x - b).^2/c.^2).*(act_x - b).^2)/c.^3;
% jacobian_d
Jf=[jacobian_a,jacobian_b,jacobian_c,jacobian_d];
gx=Jf'*r;
%(Jf'*Jf +uI)delta_abcd=Jf'f(x)
% H =Jf'*Jf
H=Jf'*Jf;
delta_abcd=inv(Jf'*Jf+u.*I)*Jf'*r;
%delta_abcd=inv(Jf'*Jf)*Jf'*r;
%Jf'*Jf+u
% g=H*delta_abc 增量方程
if norm(delta_abcd)<segma
break;
end
% 计算 pa pb pc pd
a_iterator=a+delta_abcd(1);
b_iterator=b+delta_abcd(2);
c_iterator=c+delta_abcd(3);
d_iterator=d+delta_abcd(4);
u=correction_p(act_x,delta_abcd,u,y,a_iterator,b_iterator,c_iterator,d_iterator,Jf);
a=a_iterator;
b=b_iterator;
c=c_iterator;
d=d_iterator;
end
it_y=a*exp(-(act_x-b).^2/c.^2)+d;
plot(act_x,it_y,'-');
legend('act','fit','Location','southoutside','Orientation','horizontal')
% 计算相关性
function u=correction_p(act_x,delta,u,y,a,b,c,d,Jf)
y_1=a*exp(-(act_x-b).^2/c.^2)+d;
pp=Jf*delta;
ys=y_1-y;
p=ys\pp;
if p>0.75
x=2*u;
elseif p<0.25
x=0.5*u;
end
u=x;
end 
有误请指出共同探讨!!!
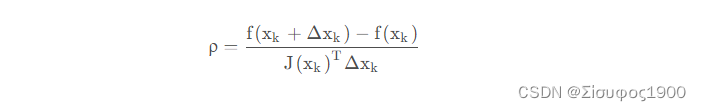








![[JS与链表]双向链表](https://img-blog.csdnimg.cn/img_convert/d7c1c5d0af9c3fd6f14a208ae67212cc.png)