LTI连续线性时不变系统能控性证明（格拉姆判据、秩判据）

news2025/1/21 12:45:25

一、能控性和能达性

1.1、能控性和能达性的定义

能控性：如果在一个有限的时间间隔内，可以用幅值没有限制的输入作用，使偏离系统平衡状态的某个初始状态回复到平衡状态，就称这个初始状态是能控的。

能达性：系统在外控制作用下能从零状态达到状态空间中任意非零状态的一种性能。

上述为能控性和能达性官方性的定义，在这里引入一个例子进行介绍：

$\begin{aligned} & x_1^{\prime}=x_1+u \\ & x_2^{\prime}=x_2 \\ & y=x_1 \end{aligned}$

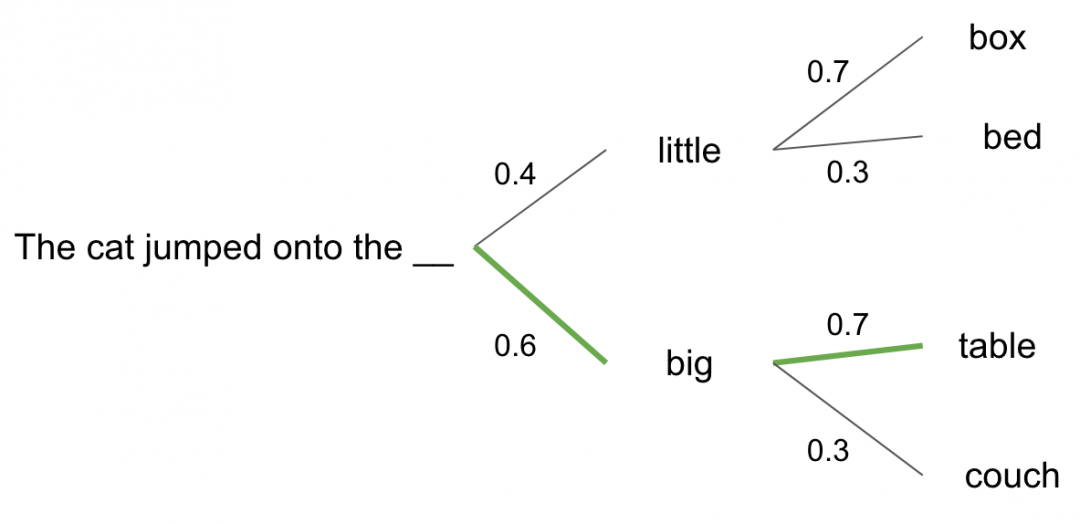
对于这样一个系统，我们发现通过控制输入u，可以改变状态 $x_1$ 和系统输出y，但是无法改变状态 $x_2$ 。此时，卡尔曼注意到了此情况，并提出特定情况：状态变为零、或从零出发到某个状态，即能控性和能达性。

对于课本中，对能控和能达，进行了如下描述：

能控：对连续时间线性时变系统 $\dot{x}=A(t) x+B(t) u , t \in J$ ，如果存在一个时刻 $\left.t_1 \in J, t_1\right\rangle t_0$ ，以及一个无约束的容许控制 $u(t) t \in\left[t_0, t_1\right]$ ，使系统状态由 $x\left(t_0\right)=x_0$ 转移到 $x\left(t_1\right)=0$ ，则称非零状态 $x_0$ 在 $t_0$ 时刻能控。

能达：如果存在一个时刻 $\mathrm{t}_1 \in \mathrm{J}, \mathrm{t}_1>\mathrm{t}_0$ ，以及一个无约束的容许控制 $\mathrm{u}(\mathrm{t}), \mathrm{t} \in\left[\mathrm{t}_0, \mathrm{t}_1\right]$ ，使系统状态由 $x\left(t_0\right)=0$ 转移到 $x\left(t_1\right)=x_f \neq 0$ ，则称非零状态 $x_f$ 在 $t_0$ 时刻为能达。

上述，无约束容许控制，主要保证了输入的 u(t)是可以实现的。此外，还有一致能控和能达，即每个时刻都是能控或能达的。

1.2、能控和能达的关系

连续线性时不变系统，可以认为能控性就等价于能达性；

离散时间的线性时不变系统和线性时变系统，如果系统矩阵是非奇异矩阵即可逆矩阵，能控性和能达性也是等价的；

连续时间线性时变系统能控性和能达性一般不等价。

二、连续时间线性时不变系统的能控判据

2.1、格拉姆矩阵判据

考虑连续时间线性时不变系统，状态方程为： $\dot{x}=A x+B u \quad x(0)=x_0 \quad t \geq 0$ 。

其中， $x$ 为 $n$ 维状态， $A$ 和 $B$ 分别为nxn和nxp维度的常值矩阵。

格拉姆判据：连续时间线性时不变系统为完全能控的充分必要条件是存在时刻 $t_1>0$ ，使格拉姆矩阵： $W_c\left[0, t_1\right] \stackrel{\Delta}{=} \int_0^{t_1} e^{-A t} B B^T e^{-A^T t} d t$ 为非奇异。

判据充分性证明：已知 $W_c\left[t_0, t_1\right]$ 为非奇异，欲证系统完全能控。设x为状态空间中任意非零状态，

构造系统输入： $u(t)=-B^T e^{-A^T t} W_c^{-1}\left[0, t_1\right] x_0, t \in\left[0, t_1\right]$

$\begin{aligned} & x\left(t_1\right)=e^{A t_1} x+\int_{t_0}^{t_1} e^{A\left(t_1-t\right)} B u(t) d t \\ & =e^{A t_1} x_0-e^{A t_1}\left\{\int_{t_0}^{t_1} e^{-A t} B B^T e^{-A^T t} d t\right\} W_c^{-1}\left[0, t_1\right] x_0 \\ & =e^{A t_1} x_0-e^{A t_1} W_c\left[0, t_1\right] W_c^{-1}\left[0, t_1\right] x_0 \\ & =e^{A t_1} x_0-e^{A t_1} x_0=0 \end{aligned}$

可证，在 $W_c$ 非奇异下，系统状态可在控制输入u下转移至为零的状态，说明系统是能控的。

判据必要性证明：欲证 $W_c\left[t_0, t_1\right]$ 为非奇异，采用反证法，设状态空间至少存在一个非零状态 $\bar{x}_0$ 使 $\bar{x}_0^T W_c\left[0, t_1\right] \bar{x}_0=0$ ，进而可以导出：

$\begin{aligned} 0 & =\bar{x}_0^T W_c\left[0, t_1\right] \bar{x}_0=\int_0^{t_1} \bar{x}_0^T e^{-A t} B B^T e^{-A^T t} \bar{x}_0 d t \\ & =\int_0^{t_1}\left[B^T e^{-A^T t} \bar{x}_0\right]^T\left[B^T e^{-A^T t} \bar{x}_0\right] d t \\ & =\int_0^{t_1}\left\|B^T e^{-A^T t} \bar{x}_0\right\|^2 d t \end{aligned}$

其中， $\|\bullet\|$ 表示所示向量的范数，而范数必为非负，于是，只能有：

$B^T e^{-A^T t} \bar{x}_0=0, \forall t \in\left[0, t_1\right]$

另一方面，由系统完全能控知，状态空间中所有非零状态均可找到相应的输入u(t)使成立：

$0=x\left(t_1\right)=e^{A t_1} \bar{x}_0+\int_0^{t_1} e^{A t_1} e^{-A t} B u(t) d t$

基此，可进而导出：

$\bar{x}_0=-\int_0^{t_1} e^{-A t} B u(t) d t$

$\left\|\bar{x}_0\right\|^2=\bar{x}_0^T \bar{x}_0=\left[-\int_0^{t_1} e^{-A t} B u(t) d t\right]^T \bar{x}_0=-\int_0^{t_1} u^T(t)\left[B^T e^{-A^T t} \bar{x}_0\right] d t$