Vector Quantisation for Robust Segmentation

摘要

背景
医学领域中分割模型的可靠性取决于模型对输入空间中扰动的鲁棒性。鲁棒性是医学成像中的一个特殊挑战，它表现出各种图像噪声、破坏和域偏移的来源。通常通过模拟异构环境来尝试获得鲁棒性，要么以数据扩充的形式启发式，要么通过学习以对抗性的方式生成特定的扰动。
方法

1. 提出并证明了在低维嵌入空间中学习离散表示可以提高分割模型的鲁棒性。
2. 这是通过一种称为矢量量化的字典学习方法实现的
3. 使用一组实验来分析潜在空间和输出空间在输入空间中的域偏移和噪声扰动下的鲁棒性
4. 调整了流行的UNet架构，在 bottleneck中插入了量化块。
   代码地址

本文方法

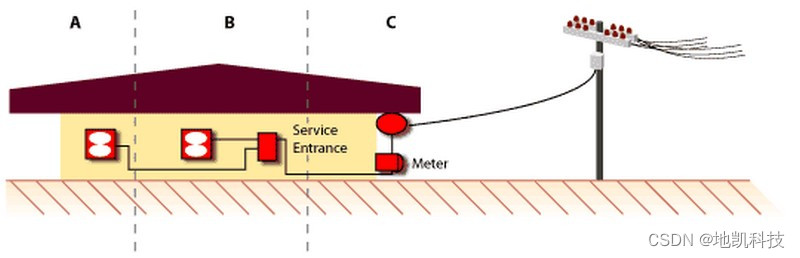
给定一个输入x，我们首先定义一个函数f（x）来表示由于扰动而变换的输入。这是一个通用函数，用于说明从重新归一化函数到非线性映射的各种类型的扰动。因此，我们现在将扰动表示为δ（x）=f（x）−x，它可以表示噪声或域偏移。这项工作的目的是找到一种方法来学习权重为w的模型（Φ），使其对δ（x）具有鲁棒性，并从扰动输入f（x）中构造一个不受干扰的分割y。
假设1：
假设δ（x）的值很小，那么我们可以用一阶泰勒展开来近似Φ（x+δ）。因此，训练框架应针对argminw[Φ（x+δ（x））−Φ（x）]进行优化，使其具有鲁棒性

假设2：
在这项工作中，我们假设分割网络可以分解为编码器（Φe）和解码器（Φd），使得Φ=Φd◦ Φe，Φe:X→ 从图像空间到低维嵌入空间的E映射和Φd:E→ Y将嵌入空间映射回分割空间

Quantisation for Robustness

形式上，通过量化块，我们的分割网络Φ现在分解为Φd◦ Φq◦ Φe，其中Φe、Φd、Φq对应于编码器、解码器和量化块
量化过程最初要求我们定义一个码本（c∈RK×D。K是码本的大小，D是每个码本向量li∈RD的维数。然后，我们定义了一个离散的一致先验，并学习了一个分类分布P（z|x），其具有一个热概率，该概率由e中的每个嵌入向量到最近的码本向量lk的映射确定，该码本向量形成zq如下

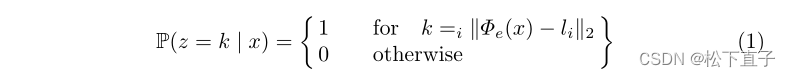
通过不可微分量化块的反向传播需要直通梯度近似，由此将梯度从zq复制到用于更新码本的编码器输出（e）。这允许使用以下损失函数对整个模型进行端到端的训练


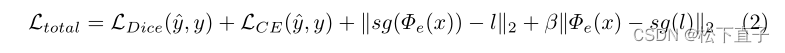
我们假设如果||Φe（x）−li||2 > 0; 则x受到δ（x）的绝对扰动。这意味着维度为D的码本c包含最小数量的码本向量K，以完全捕获潜在空间中的所有可能语义，即完整语义。我们还假设c均匀分布在D维超球面的表面上。因此，位于c之间的超球面上的空间只表示c的扰动。我们将超球面的整个表面表示为Z，Φe（x）只生成仅位于Z上的e

最后，如果解码器（Φd）只是量化表示（zq）的函数，那么给出我们的假设3，Φ（x+δ（x））=Φ（x）。然而，如果Φd是z和编码器每个标度的输出的函数，就像在UNet中一样，那么δ（x）对模型输出的影响只会减少。然而，在代码本不完整的情况下，这在实践中可能是有益的。

Perturbation Bounds

在假设3的情况下，码本的优点是允许我们导出潜在空间中的偏移的极限，该极限表示扰动和我们采样的数据分布的真正语义偏移之间的边界。这可以定义为单个码本矢量周围允许的最大扰动，表示为r，并根据经验计算为整个c上码本矢量（li）与其最近邻居（li+1）之间平均距离的一半，如下所示：

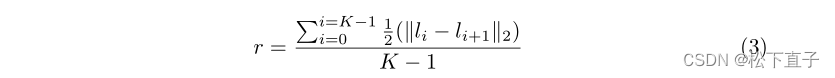
接下来，为了简单起见，从Φe（x）和Φe（x+δ（x））的输出中观察单个向量，表示为ej和ej+Δ。我们可以将方程3和Φe（x+δ（x））的一阶泰勒展开式结合起来，将r理论上表示为Δ（x），如下所示：

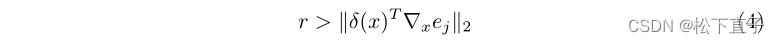
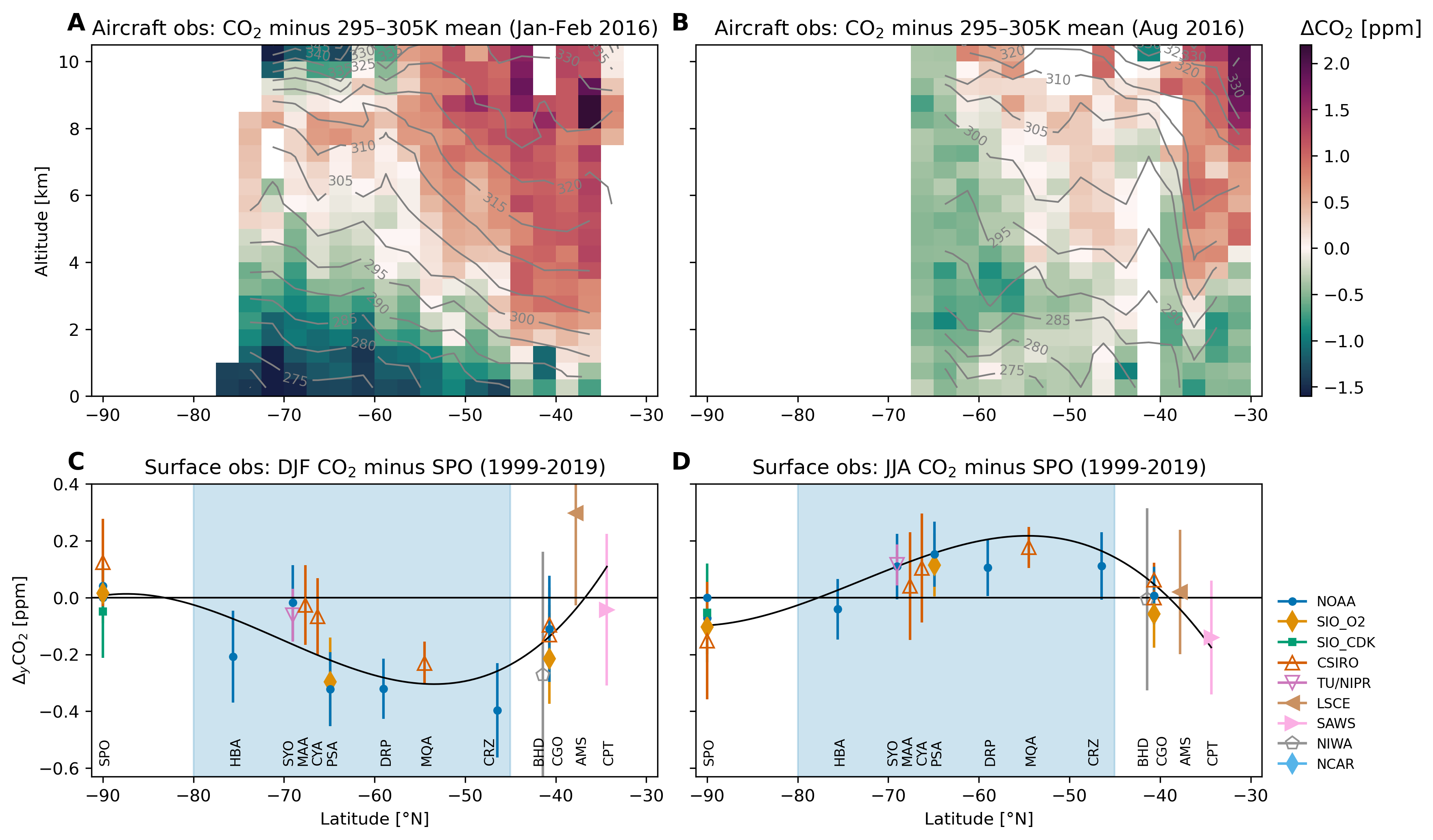
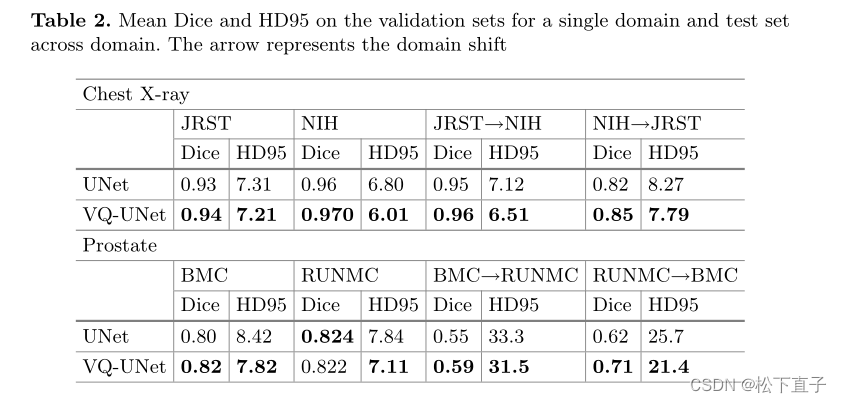
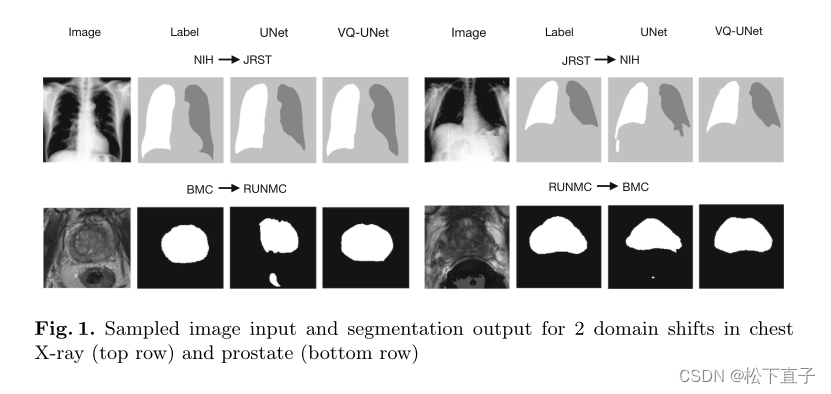
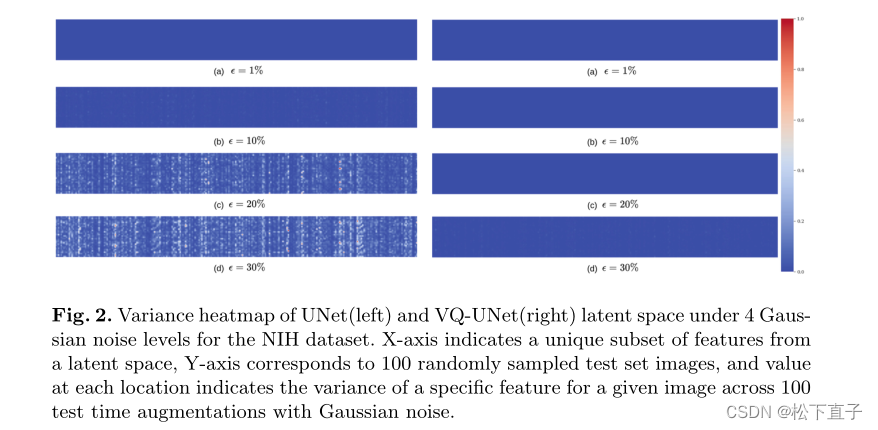
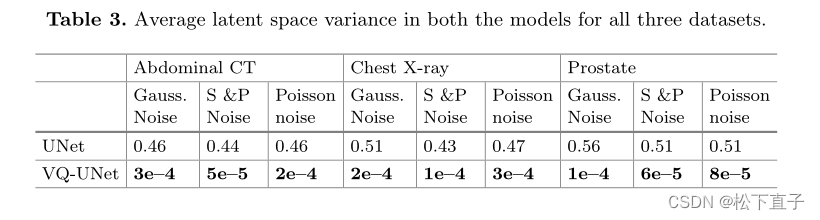
实验结果