Python BP算法模板

news2024/11/27 0:48:11

BP算法模板

神经网络结构

三大基本结构

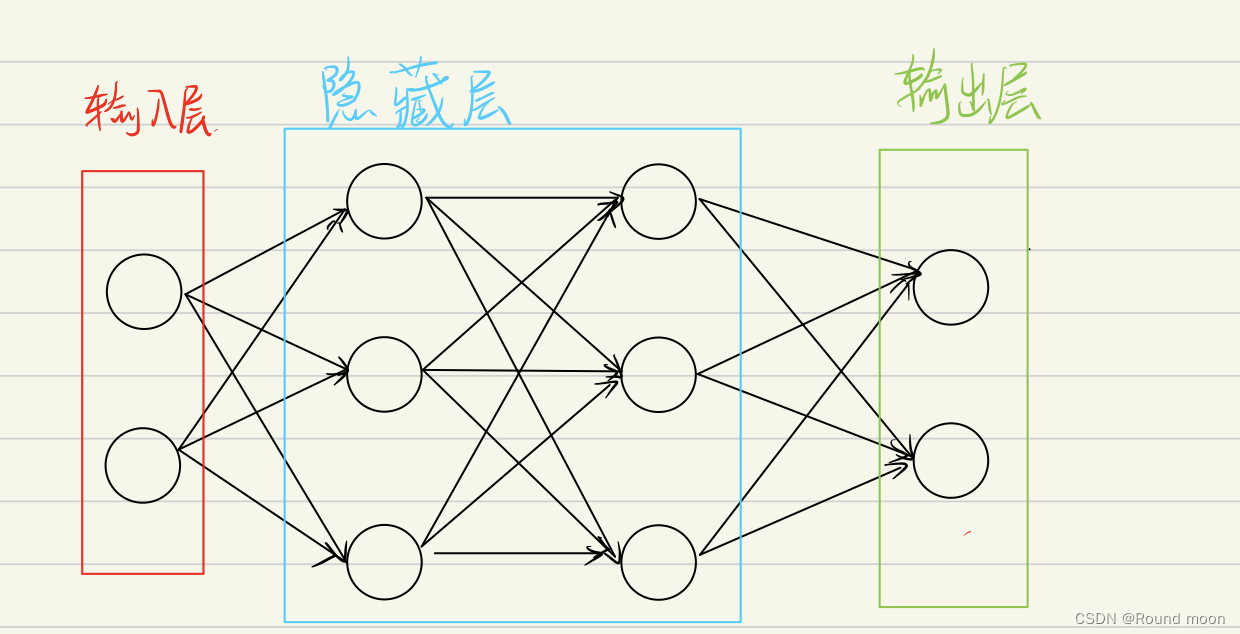
请添加图片描述

权重(轴突、树突)

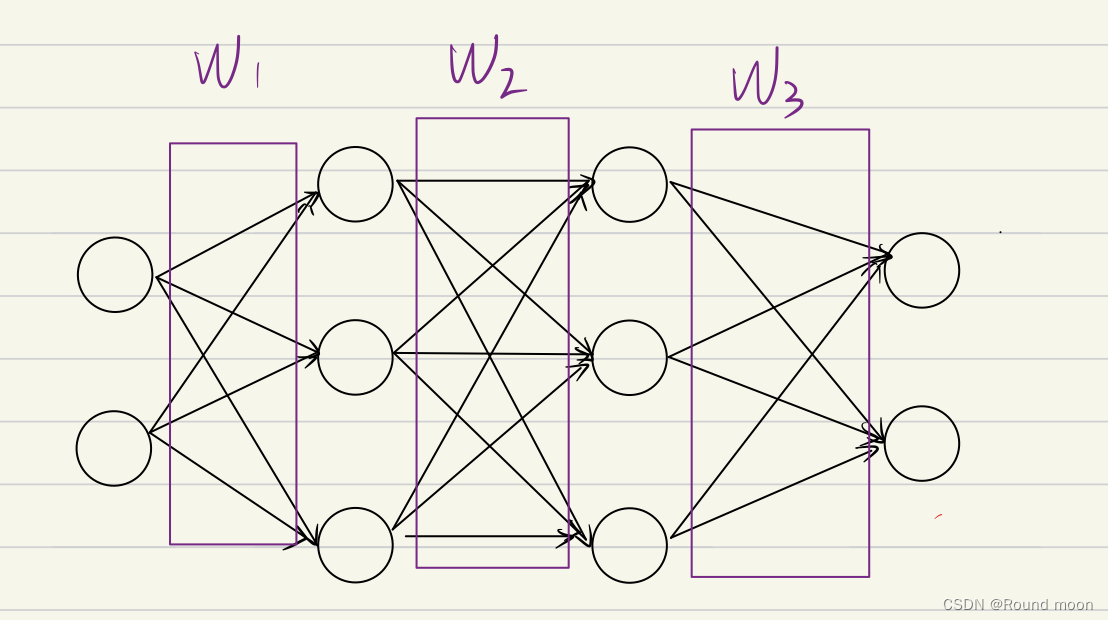
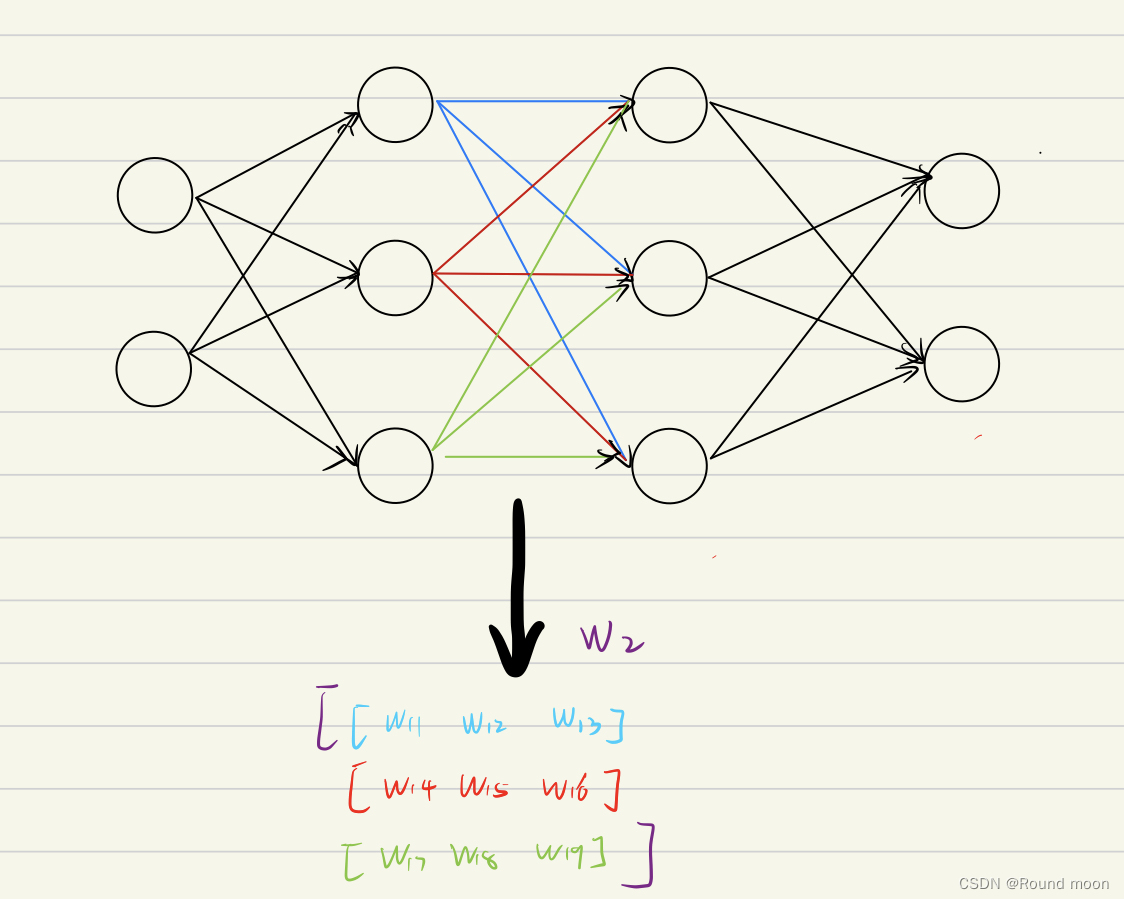
请添加图片描述

权重的矩阵表示

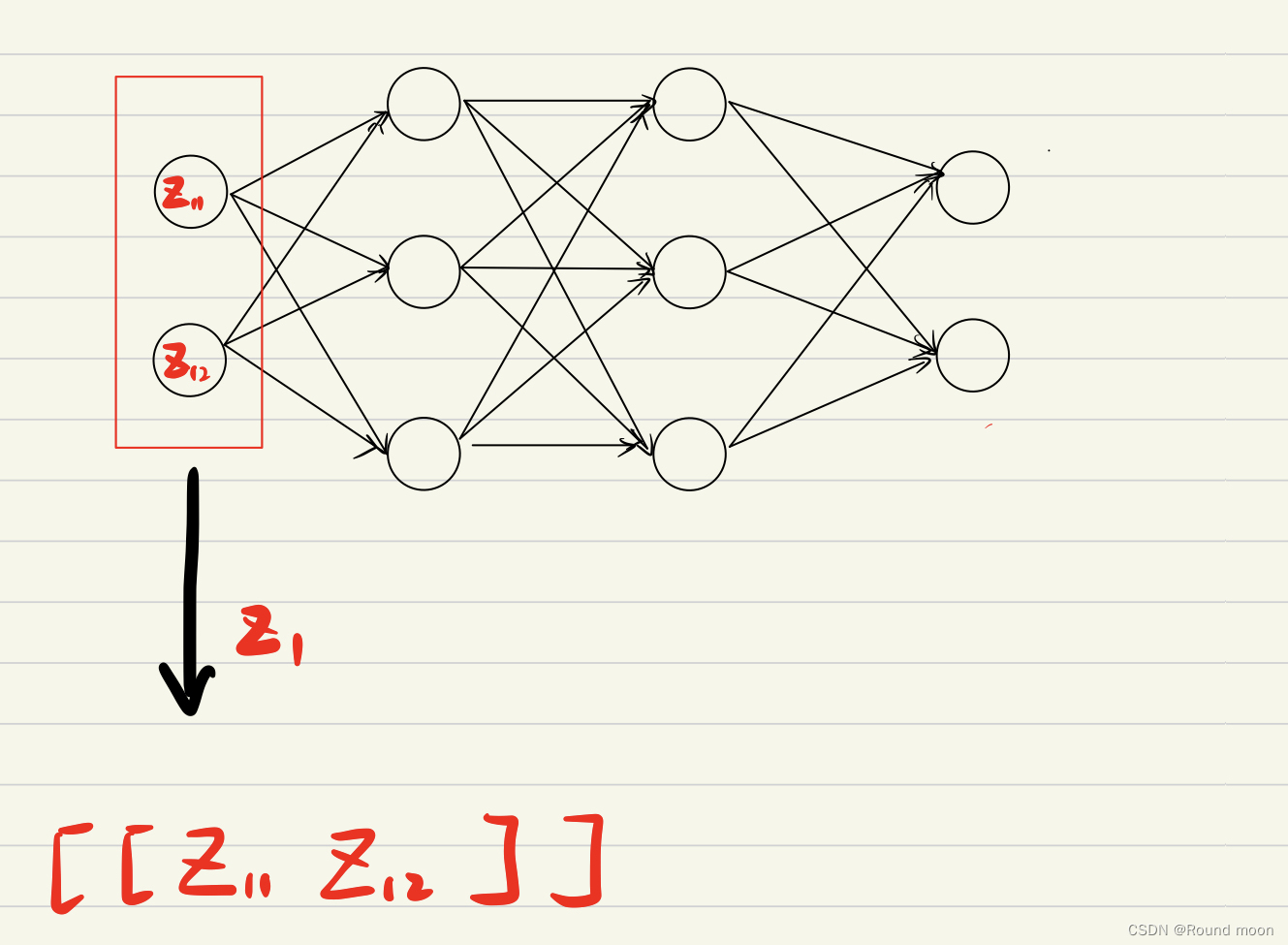
请添加图片描述

数值(胞体)

请添加图片描述

数值处理方式

sigmoid 函数

def __sigmoid(self,x):
    return 1 / (1 + np.exp(-x))

sigmoid 的导函数

def __sigmoid_prime(self,x):
    return x * (1 - x)

sigmoid 函数图像

请添加图片描述
其目的是将数值限制其大小输出。简单理解为一个阀门，当数值足够大时，标记为1。

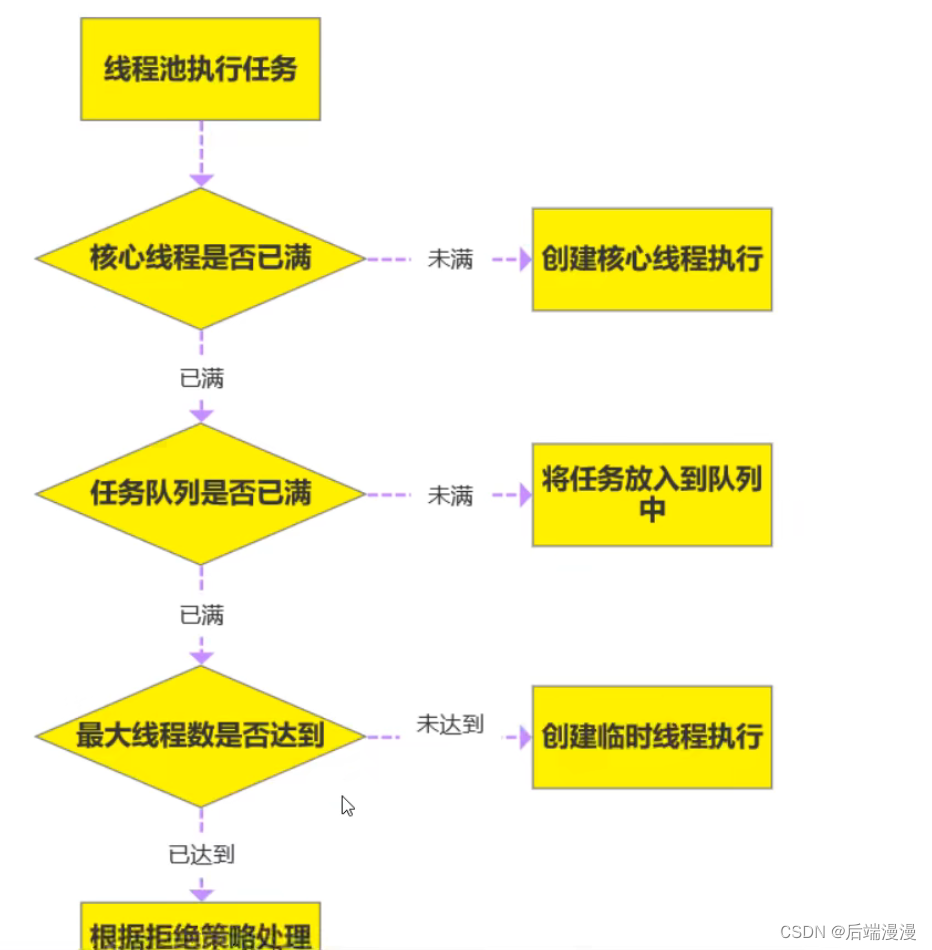
核心运算

前向运算

def forward(self,X):
    self.Z.clear()
    X=np.array(X)
    self.Z.append(self.__sigmoid(np.dot(X,self.W[0])+self.B[0]))
    for i in range(2,len(self.Size)):
        self.Z.append(self.__sigmoid(np.dot(self.Z[-1],self.W[i-1])+self.B[i-1]))
    return self.Z[-1]

每个神经元的值乘以权重，累加到目标神经元中

反馈运算

def backward(self,X,Y,ans,Lambda ):
    dw=[]
    db=[]
    error = ans-Y
    delta = error * self.__sigmoid_prime(Y)
    dw.insert(0,np.dot(self.Z[-2].T, delta))
    db.insert(0,np.sum(delta, axis=0, keepdims=True))
    for i in range(1,len(self.Size)-2):
        delta = np.dot(delta, self.W[-i].T) * self.__sigmoid_prime(self.Z[-1-i])
        dw.insert(0,np.dot(self.Z[-2-i].T, delta))
        db.insert(0,np.sum(delta, axis=0, keepdims=True))
    delta = np.dot(delta, self.W[1].T) * self.__sigmoid_prime(self.Z[0])
    dw.insert(0,np.dot(X.T, delta))
    db.insert(0,np.sum(delta, axis=0, keepdims=True))
    for i in range(len(dw)):
        self.W[i]+=dw[i]*Lambda
        self.B[i]+=db[i]*Lambda
    return sum(error[0])

代码看起来有些凌乱，这里总结一下整体思路
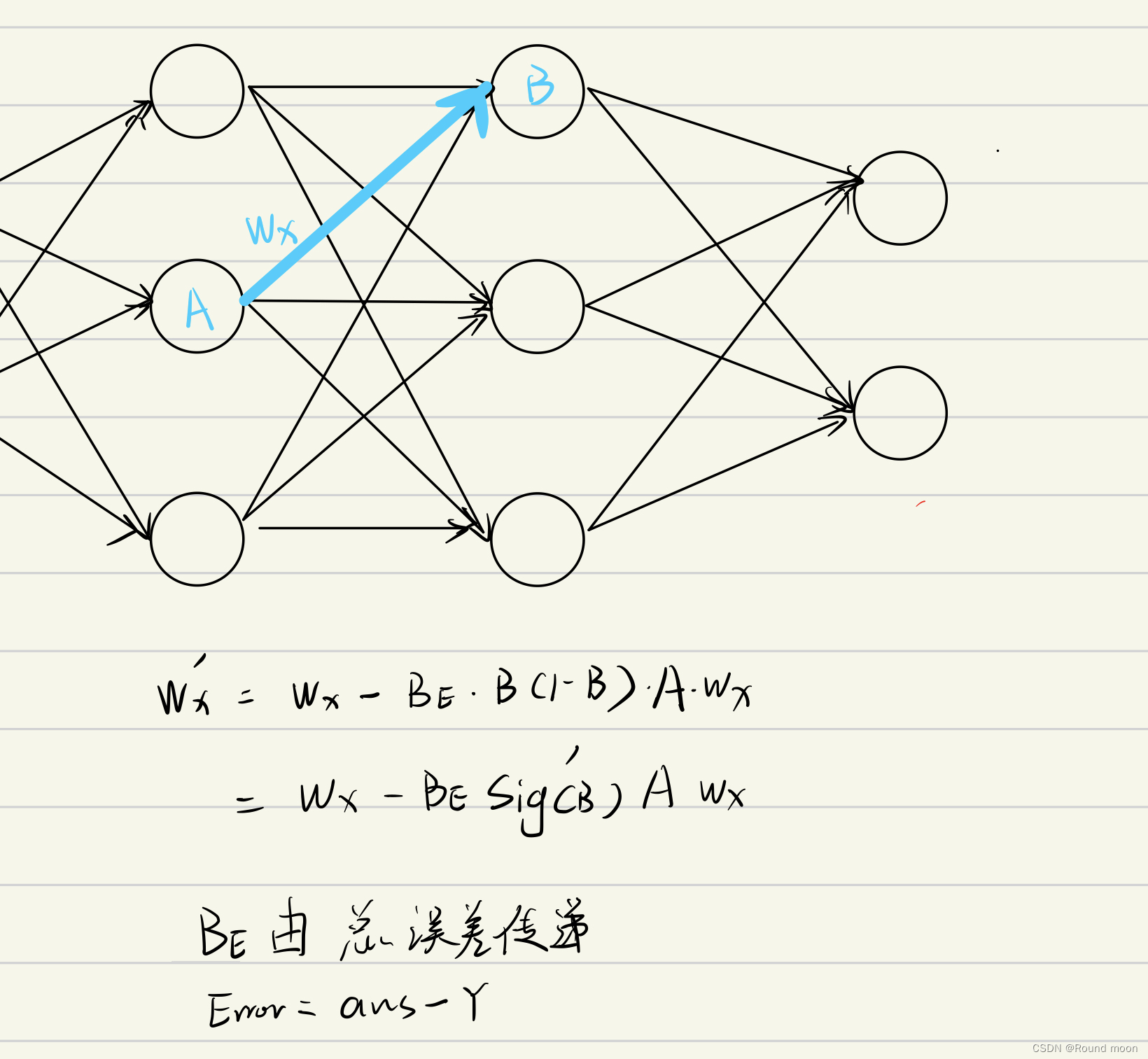
请添加图片描述
针对每一个权重的调整策略，就是由
d w = 误差 × 右亮 × ( 1 − 右亮 ) × 左亮 × 原始权重 dw = 误差\times右亮\times(1-右亮)\times左亮\times原始权重 dw=误差×右亮×(1−右亮)×左亮×原始权重
决定的。
这里重点说一下，原始公式要求是减法，但是考虑到误差的符号可以传递，那么在一开始的误差就做一下修改，改为误差的相反数，即 E r r o r = a n s − Y Error=ans-Y Error=ans−Y
一般情况下，神经网络还需要一个常量的节点参与，所以每个神经元都有一个常量的参数 B。
对于 dB 的求法，其实就是误差梯度之和。
以上最重要的就是理解一下，这段代码的核心思路，具体细节还是要看代码。这里代码已经将正负调整过了，代码中看到的就是调整后的。
这里的Lambda 是学习力度，当获得一个新的知识点后，我们可以通过调整修改的力度。防止学傻了。

使用

Net=Neural([3,15,15,15,2])

这里传入一个结构列表，第一位代表输入层的结构，最后一位代表输出层结构，里面均是隐藏层的结构。

X,ans=Net.Format_Input([a,b,c],ans)

这里是根据输入层的结构个数，和输出层的结构个数，输入一个列表，做一下格式化。

Y=Net.forward(X)
E=Net.backward(X,Y,ans,0.01)

Y做为接收，获得输出层的输出结果，E做为误差值，目的是直观的感受训练的变化。

def creat(self):
    for i in range(1,len(self.Size)):
        self.W.append(np.random.randn(self.Size[i-1],self.Size[i]))
    for i in range(1,len(self.Size)):
        self.B.append(np.ones((1,self.Size[i])))

这里在网络训练之出，根据结构创建出整体框架，并随机赋值。
接下来我们也可以存储结构，因为一个网络知道结构后最重要的就是权重值，我们只需要把权重值存储一下，我们就可以接着上次继续运行了。

代码示例

聚类示例

import numpy as np
class Neural:
    def __init__(self,Size):
        self.Z=[]
        self.W=[]
        self.B=[]
        self.Size=Size
    def __sigmoid(self,x):
        return 1 / (1 + np.exp(-x))
    def __sigmoid_prime(self,x):
        return x * (1 - x)
    def Format_Input(self,NetIn,NetOut):
        return np.array([NetIn]),np.array([NetOut])
    def creat(self):
        for i in range(1,len(self.Size)):
            self.W.append(np.random.randn(self.Size[i-1],self.Size[i]))
        for i in range(1,len(self.Size)):
            self.B.append(np.ones((1,self.Size[i])))
        
    def forward(self,X):
        self.Z.clear()
        X=np.array(X)
        self.Z.append(self.__sigmoid(np.dot(X,self.W[0])+self.B[0]))
        for i in range(2,len(self.Size)):
            self.Z.append(self.__sigmoid(np.dot(self.Z[-1],self.W[i-1])+self.B[i-1]))
        return self.Z[-1]
    def backward(self,X,Y,ans,Lambda ):
        dw=[]
        db=[]
        error = ans-Y
        delta = error * self.__sigmoid_prime(Y)
        dw.insert(0,np.dot(self.Z[-2].T, delta))
        db.insert(0,np.sum(delta, axis=0, keepdims=True))
        for i in range(1,len(self.Size)-2):
            delta = np.dot(delta, self.W[-i].T) * self.__sigmoid_prime(self.Z[-1-i])
            dw.insert(0,np.dot(self.Z[-2-i].T, delta))
            db.insert(0,np.sum(delta, axis=0, keepdims=True))
        delta = np.dot(delta, self.W[1].T) * self.__sigmoid_prime(self.Z[0])
        dw.insert(0,np.dot(X.T, delta))
        db.insert(0,np.sum(delta, axis=0, keepdims=True))
        for i in range(len(dw)):
            self.W[i]+=dw[i]*Lambda
            self.B[i]+=db[i]*Lambda
        return sum(error[0])
from random import randint as rand
Net=Neural([3,15,15,15,2])
Net.creat()
for i in range(1000000):
    #数据
    if rand(1,2)==1:
        a=rand(1,50)
        b=rand(20,30)
        c=rand(1,5)
        ans=[1,0]
    else:
        a=rand(51,100)
        b=rand(10,20)
        c=rand(6,8)
        ans=[0,1]
    #核心
    X,ans=Net.Format_Input([a,b,c],ans)
    Y=Net.forward(X)
    E=Net.backward(X,Y,ans,0.01)
    #验证
    if i%10000==0:
        print(i,"%.5f"%E)

这是一个聚类的神经网络，我们训练好网络后，我们可以走一遍，forward，获得输出，通过输出的特点去判断机器的决策结果。下面给出直观看出百分比的代码模块。

from random import randint as rand
Net=Neural([3,15,15,15,2])
Net.creat()
for i in range(100000):
    if rand(1,2)==1:
        a=rand(1,50)
        b=rand(20,30)
        c=rand(1,5)
        ans=[1,0]
    else:
        a=rand(51,100)
        b=rand(10,20)
        c=rand(6,8)
        ans=[0,1]
    X=np.array([[a,b,c]])
    Y=Net.forward(X)
    ans=np.array([ans])
    Net.backward(X,Y,ans,0.05)
    if i%10000==0:
        print(i,end=" ")
        cnt=0
        for i in range(100):
            if rand(1,2)==1:
                a=rand(1,50)
                b=rand(20,30)
                c=rand(1,5)
                ans=[1,0]
            else:
                a=rand(51,100)
                b=rand(10,20)
                c=rand(6,8)
                ans=[0,1]
            X=np.array([[a,b,c]])
            Y=Net.forward(X)
            if Y[0][0]>Y[0][1]:
                if ans==[1,0]:
                    cnt+=1
            else:
                if ans==[0,1]:
                    cnt+=1
        print(cnt)

比较大小示例

import numpy as np
class Neural:
    def __init__(self,Size):
        self.Z=[]
        self.W=[]
        self.B=[]
        self.Size=Size
    def __sigmoid(self,x):
        return 1 / (1 + np.exp(-x))
    def __sigmoid_prime(self,x):
        return x * (1 - x)
    def Format_Input(self,NetIn,NetOut):
        return np.array([NetIn]),np.array([NetOut])
    def creat(self):
        for i in range(1,len(self.Size)):
            self.W.append(np.random.randn(self.Size[i-1],self.Size[i]))
        for i in range(1,len(self.Size)):
            self.B.append(np.ones((1,self.Size[i])))
        
    def forward(self,X):
        self.Z.clear()
        X=np.array(X)
        self.Z.append(self.__sigmoid(np.dot(X,self.W[0])+self.B[0]))
        for i in range(2,len(self.Size)):
            self.Z.append(self.__sigmoid(np.dot(self.Z[-1],self.W[i-1])+self.B[i-1]))
        return self.Z[-1]
    def backward(self,X,Y,ans,Lambda ):
        dw=[]
        db=[]
        error = ans-Y
        delta = error * self.__sigmoid_prime(Y)
        dw.insert(0,np.dot(self.Z[-2].T, delta))
        db.insert(0,np.sum(delta, axis=0, keepdims=True))
        for i in range(1,len(self.Size)-2):
            delta = np.dot(delta, self.W[-i].T) * self.__sigmoid_prime(self.Z[-1-i])
            dw.insert(0,np.dot(self.Z[-2-i].T, delta))
            db.insert(0,np.sum(delta, axis=0, keepdims=True))
        delta = np.dot(delta, self.W[1].T) * self.__sigmoid_prime(self.Z[0])
        dw.insert(0,np.dot(X.T, delta))
        db.insert(0,np.sum(delta, axis=0, keepdims=True))
        for i in range(len(dw)):
            self.W[i]+=dw[i]*Lambda
            self.B[i]+=db[i]*Lambda
        return sum(error[0])
from random import randint as rand
Net=Neural([2,15,15,15,1])
Net.creat()
for i in range(1000000):
    #数据
    a=rand(1,50)
    b=rand(1,50)
    ans=[1] if a>b else [0]
    #核心
    X,ans=Net.Format_Input([a,b],ans)
    Y=Net.forward(X)
    E=Net.backward(X,Y,ans,0.01)
    #验证
    if i%10000==0:
        print(i,"%.5f"%E,end=" ")
        cnt=0
        for j in range(1000):
            a=rand(1,50)
            b=rand(1,50)
            ans=[1] if a>b else [0]
            X,ans=Net.Format_Input([a,b],ans)
            Y=Net.forward(X)
            if (Y[0][0]-ans)<0.1:
                cnt+=1
        print("%%%.2f"%(cnt/1000*100))

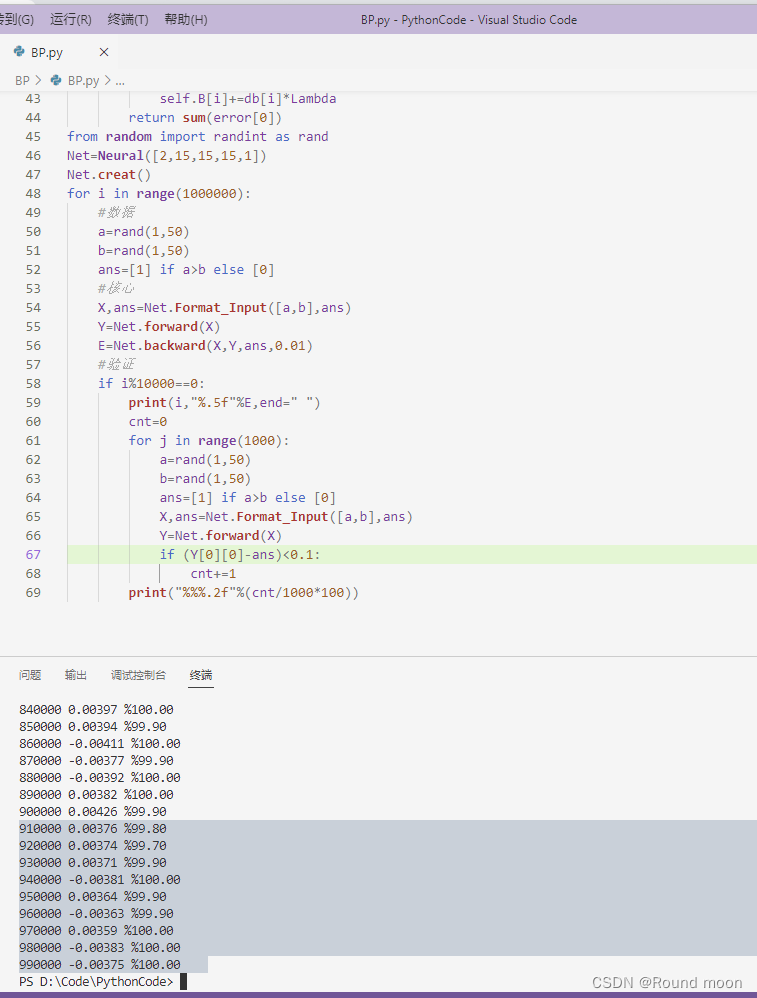
在这里插入图片描述
我们可以看到，这里训练的结果其实很乐观，我们把要求提的苛刻了一些，回出现%99.5-%100之间的波动，而且波动其实也不是很大。
或者我们调整一下学习力度，有可能是之前学的太慢了。
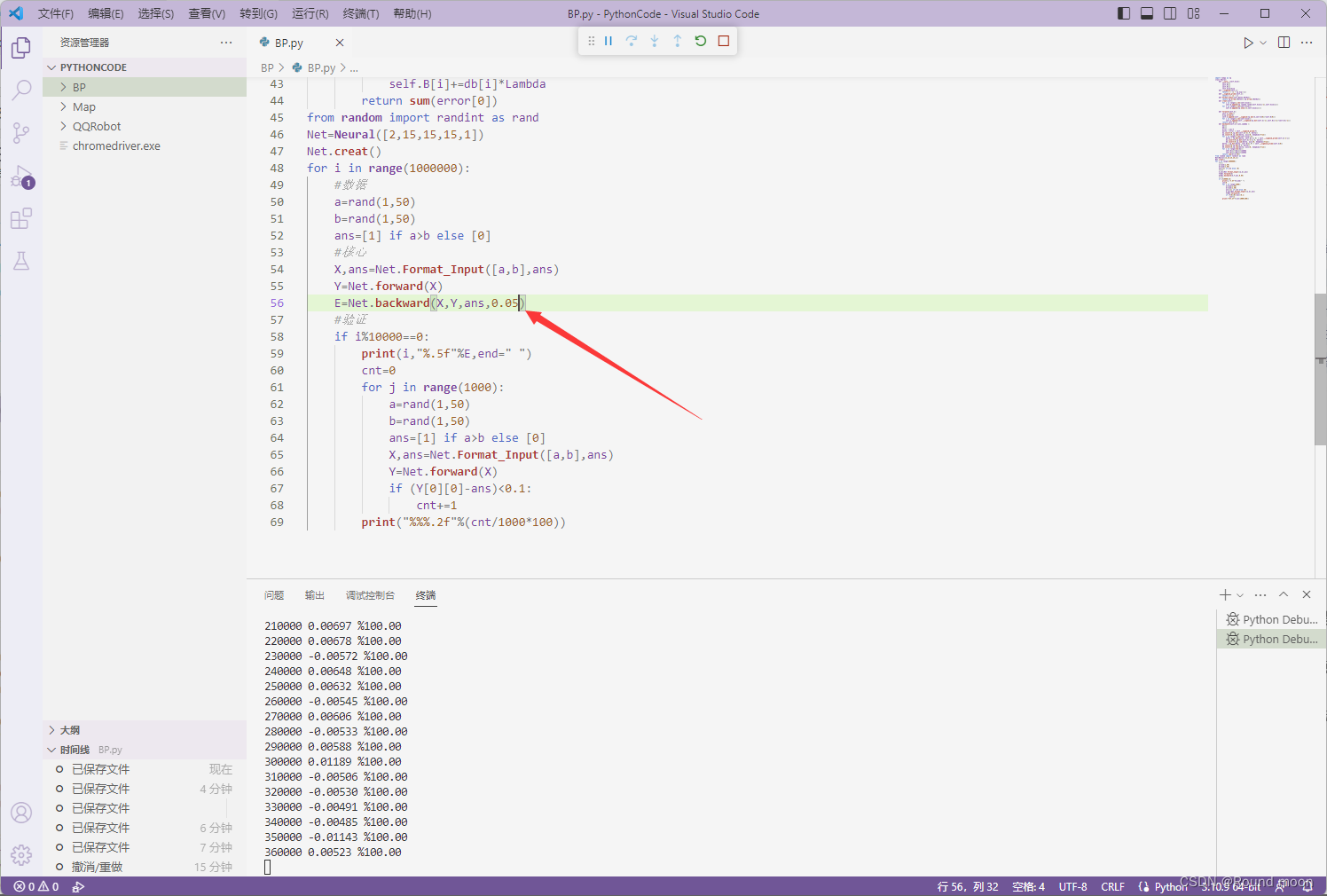
在这里插入图片描述

将学习力度，从0.01改为0.05，效果直接好了很多。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/525103.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java多线程synchronized Lock volatile，看完这一篇就够了

Java多线程synchronized Lock volatile，看完这一篇就够了

线程安全问题 一、对线程安全的理解&#xff08;实际上是内存安全&#xff09;二、线程同步的实现方法synchronized实现同步Lock实现同步volatile实现同步JUC的Callable实现同步 三、守护线程四、ThreadLocal原理和使用场景五、Thread类的常用方法&#xff0c;以及线程的状态六…
阅读更多...
Linux下使用Mysql 第二天

Linux下使用Mysql 第二天

目录 Mysql数据库API库 编写hello应用链接函数库 MySQL API常用函数 总体印象 初始化 Makefile 管理 连接数据库关闭连接 读取数据 查询表数据 获取结果集 解析结果集 释放结果集 获取列数 获取表头 实例程序 MySQL tools实现 思路分析 程序实现 中文问题 …
阅读更多...
MS iCraft Z790ITX WIFI 电脑 Hackintosh 黑苹果efi引导文件

MS iCraft Z790ITX WIFI 电脑 Hackintosh 黑苹果efi引导文件

原文来源于黑果魏叔官网&#xff0c;转载需注明出处。&#xff08;下载请直接百度黑果魏叔&#xff09; 硬件型号驱动情况 主板MS iCraft Z790ITX WIFI 处理器Intel Core i5-13400已驱动 内存Asgard DDR5 6400CL32 16GBx2 RGB已驱动 硬盘西数 WDS250G3X0C-00SJG0 ( SN750) …
阅读更多...
如何设计API返回码（错误码）？

如何设计API返回码（错误码）？

一、前言 客户端请求 API&#xff0c;通常需要通过返回码来判断 API 返回的结果是否符合预期&#xff0c;以及该如何处理返回的内容等 相信很多同学都吃过返回码定义混乱的亏&#xff0c;有的 API 用返回码是 int 类型&#xff0c;有的是 string 类型&#xff0c;有的用 0 表…
阅读更多...
ansible 常用用例

ansible 常用用例

目录 一、说明 二、创建 ansible 环境 三、实验操作 四、install_ansible.sh 脚本内容 一、说明 该文档是日常经常使用的模板&#xff0c;通过该例子让更多的初学者了解ansible 剧本的写法&#xff0c;很多情况&#xff0c;可以按照该模版来套用即可。 读者不需要下载…
阅读更多...
6.深入理解Mysql事务隔离级别与锁机制

6.深入理解Mysql事务隔离级别与锁机制

MySQL性能调优 1. 概述2. 事务及其ACID属性2.1并发事务带来的问题2.2 事务隔离级别 3. 锁详解3.1 锁分类3.1.1 表锁3.1.2 行锁3.1.3 间隙锁(Gap Lock)3.1.4 临键锁(Next-key Locks)3.1.5 行锁分析3.1.6 查看INFORMATION_SCHEMA系统库锁相关数据表3.1.7 死锁3.1.8 锁优化建议 4.…
阅读更多...
iOS - postgetAFNetworking

iOS - postgetAFNetworking

GET和POST HTTP定义了与服务器交互的不同方法&#xff0c;最基本的方法有4种&#xff0c;分别是GET&#xff0c;POST&#xff0c;PUT&#xff0c;DELETE。URL全称是资源描述符&#xff0c;我们可以这样认为&#xff1a;一个URL地址&#xff0c;它用于描述一个网络上的资源&…
阅读更多...
OpenGL高级-实例化

OpenGL高级-实例化

知识点 假如你有一个有许多模型的场景&#xff0c;而这些模型的顶点数据都一样&#xff0c;只是进行了不同的世界空间的变换。想象一下&#xff0c;有一个场景中充满了草叶&#xff1a;每根草都是几个三角形组成的。你可能需要绘制很多的草叶&#xff0c;最终一次渲染循环中就肯…
阅读更多...
每日一练 | 华为认证真题练习Day45

每日一练 | 华为认证真题练习Day45

1、应用数据经过数据链路层处理后一定携带了MAC地址。 A. 对 B. 错 2、某网络工程师在输入命令行时提示如下信息&#xff1a; Error:Unrecognized command found at’^’position. 对于该提示信息说法正确的是&#xff1f; A. 输入命令不完整 B. 没有查找到关键字 C. 输…
阅读更多...
LeetCode 1054 距离相等的条形码

LeetCode 1054 距离相等的条形码

LeetCode 1054 距离相等的条形码 来源&#xff1a;力扣&#xff08;LeetCode&#xff09; 链接&#xff1a;https://leetcode.cn/problems/distant-barcodes 博主Github&#xff1a;https://github.com/GDUT-Rp/LeetCode 题目&#xff1a; 在一个仓库里&#xff0c;有一排条…
阅读更多...
二叉树总结

二叉树总结

文章目录 树需要掌握的基本概念二叉树基本特点满二叉树性质 完全二叉树性质 二叉搜索树&#xff08;二叉排序树&#xff09;Binary Search Tree(BST)性质 平衡二叉树性质 红黑树五大性质 B树 二叉树的存储方式链式存储顺序存储 二叉树的遍历 树需要掌握的基本概念 1、节点、根…
阅读更多...
Python+Requests+Pytest+YAML+Allure实现接口自动化

Python+Requests+Pytest+YAML+Allure实现接口自动化

本项目实现接口自动化的技术选型&#xff1a;PythonRequestsPytestYAMLAllure &#xff0c;主要是针对之前开发的一个接口项目来进行学习&#xff0c;通过 PythonRequests 来发送和处理HTTP协议的请求接口&#xff0c;使用 Pytest 作为测试执行器&#xff0c;使用 YAML 来管理测…
阅读更多...
如何成为Apache项目贡献者

如何成为Apache项目贡献者

要成为Apache Foundation的贡献者&#xff0c;您需要遵循以下步骤&#xff1a; 加入Apache社区&#xff1a;您需要加入Apache社区并成为一个活跃的成员。您可以通过订阅邮件列表、参加会议、参加社区活动等方式来加入社区。选择一个项目&#xff1a;您需要选择一个您感兴趣的A…
阅读更多...
libevent高并发网络编程 - 03_bufferevent filter过滤器

libevent高并发网络编程 - 03_bufferevent filter过滤器

文章目录 1. bufferevent_filter过滤器简介2. evbuffer2.1 evbuffer常用API2.2 evbuffer和bufferevent的区别 3. bufferevent filter过滤器常用API3.1 bufferevent_filter_new() 4 bufferevent filter 过滤器例子 1. bufferevent_filter过滤器简介 bufferevent filter是libeve…
阅读更多...
探索LeetCode【0010】正则表达式匹配（未懂）

探索LeetCode【0010】正则表达式匹配（未懂）

目录 0.1 题目0.2 补充示例1. 参考B站视频2. 官方答案的评论-可用3. chatGPT的思路和解法-可用 0.1 题目 题目链接&#xff1a;【0010】正则表达式匹配 给你一个字符串 s 和一个字符规律 p&#xff0c;请你来实现一个支持 . 和 * 的正则表达式匹配。 . 匹配任意单个字符* 匹…
阅读更多...
UG NX二次开发（C++）-建模-删除对象

UG NX二次开发（C++）-建模-删除对象

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 1、前言2、在UG NX中创建一些测试对象3、查询这些对象的继承关系3、基于C创建的方法3.1 头文件3.2 声明删除对象的方法3.3 定义删除对象的方法3.4 填写调用代码 4、…
阅读更多...
Vue电商项目--开发Search模块

Vue电商项目--开发Search模块

Search模块的静态组件 search模块开发&#xff1f; 1.先静态页面静态组件拆分出来 2.发请求&#xff08;API&#xff09; 3.vuex&#xff08;三连环&#xff09; 4.组件获取仓库数据&#xff0c;动态展示数据 拆分静态组件&#xff0c;之前搞过。现在就不搞了&#xff0c;…
阅读更多...
STL之迭代器

STL之迭代器

文章目录 什么是迭代器&#xff1f;迭代器的作用&#xff1a;为什么要使用迭代器&#xff1f;vector容器中迭代器应该怎么使用迭代器失效插入元素后失效删除元素后失效 什么是迭代器&#xff1f; 迭代器是一种检查容器内元素并且遍历容器内匀速的数据类型 迭代器的作用&#…
阅读更多...
微服务之服务容错

微服务之服务容错

Informal Essay By English Share a sentence that I think is very reasonable, as long as you can know the underlying logic of anything, you can hold it without fear 参考书籍&#xff1a; “凤凰架构” 引言 在 Martin Fowler 与 James Lewis合写的文章《Micros…
阅读更多...
从立项到发布仅三个月，开源技术问答社区 Answer 是如何诞生的？

从立项到发布仅三个月，开源技术问答社区 Answer 是如何诞生的？

在祁宁家里&#xff0c;有一套完整的赛车模拟器&#xff0c;他甚至还请人到国外代购了最新的 VR 设备。作为沉浸式赛车游戏发烧友&#xff0c;除了享受速度与激情带来的愉悦感&#xff0c;祁宁在玩的过程中更多的是思考如何将技术能力进行产品化的问题。 Answer.dev 就是将技术…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023