LeetCode 1054 距离相等的条形码

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/distant-barcodes

博主Github：https://github.com/GDUT-Rp/LeetCode

题目：

在一个仓库里，有一排条形码，其中第 i 个条形码为 barcodes[i]。

请你重新排列这些条形码，使其中任意两个相邻的条形码不能相等。 你可以返回任何满足该要求的答案，此题保证存在答案。

示例 1:

输入：barcodes = [1,1,1,2,2,2]
输出：[2,1,2,1,2,1]

示例 2:

输入：barcodes = [1,1,1,1,2,2,3,3]
输出：[1,3,1,3,2,1,2,1]

示例 3:

输入：matrix = [[7,8],[1,2]]
输出：[7]

提示：

• 1 <= barcodes.length <= 10000
• 1 <= barcodes[i] <= 10000

解题思路：

方法一：频数表取剩余最多元素

将数据整理出<number, count>的频数表，每次取的时候取剩余最多的值，思路可行但耗时过大，是一个会超时的算法。

Golang

func rearrangeBarcodes(barcodes []int) []int {
    numCount := make(map[int]int)
    for _, code := range(barcodes) {
        numCount[code] += 1
    }
    
    var codes []int
    for i, _ := range(barcodes) {
        if i == 0 {
            codes = append(codes, peakMaxCountNum(0, numCount))
            continue
        }
        codes = append(codes, peakMaxCountNum(codes[i - 1], numCount))
    }

    return codes
}

func peakMaxCountNum(code int, numCount map[int]int) int {
    var (
        selectNum int
        selectNumCount int
    )
    for num, count := range(numCount) {
        if selectNumCount > count {
            continue
        }
        if num != code {
            selectNum = num
            selectNumCount = count
        }
    }
    numCount[selectNum] -= 1
    return selectNum
}

复杂度分析

时间复杂度：$O(n^2)$。

空间复杂度：$O(n)$，1个map的空间。

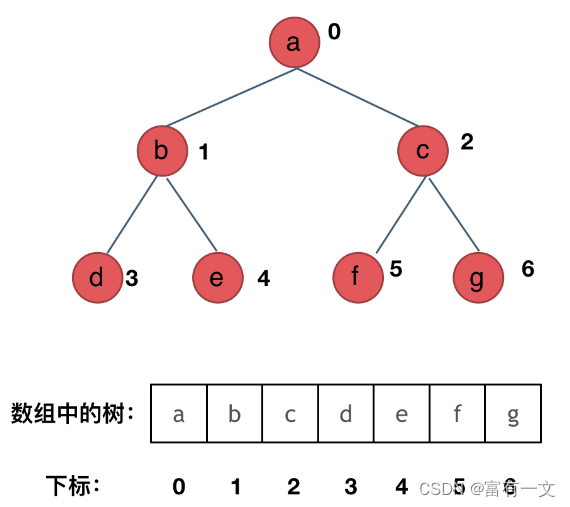
方法二：最大堆

思路与方法一差不多，但是用了最大堆来存储，利用这个数据结构可以将“取剩余最多的元素”的 $N$ 变成 $\log N$。

统计频数表，插入最大堆，这样堆顶就是剩余元素最多的元素。
然后我们每次从堆顶拿出一个剩余最多的元素，放入排序中，再更新剩余数量，重新放入最大堆中。如果这个元素与排列结果中的最后一个元素相同，那么我们就需要再从最大堆中取出第二多的元素，放入排序中，之后再把这两个元素放入最大堆中。

Golang

type PriorityQueue [][]int

func (pq PriorityQueue) Len() int {
    return len(pq)
}

func (pq PriorityQueue) Less(i, j int) bool {
    return pq[i][0] > pq [j][0]
}

func (pq PriorityQueue) Swap(i, j int) {
    pq[i], pq[j] = pq[j], pq[i]
}

func (pq *PriorityQueue) Push(x interface{}) {
    item := x.([]int)
    *pq = append(*pq, item)
}

func (pq *PriorityQueue) Pop() interface{} {
    old := *pq
    n := len(old)
    item := old[n-1]
    *pq = old[:n-1]
    return item
}

func rearrangeBarcodes(barcodes []int) []int {
    count := make(map[int]int)
    for _, b := range barcodes {
        count[b]++
    }

    q := &PriorityQueue{}
    heap.Init(q)
    for k, v := range count {
        heap.Push(q, []int{v, k})
    }

    n := len(barcodes)
    res := make([]int, n)

    for i := 0; i < n; i++ {
        p := heap.Pop(q).([]int)
        count, num := p[0], p[1]
        if i == 0 || res[i-1] != num {
            // 第一个元素符合的情况下
            res[i] = num
            if count > 1 {
                heap.Push(q, []int{count-1, num})
            }
            continue
        }
        // 与前一元素相同的情况，再取一个出来
        p2 := heap.Pop(q).([]int)
        count2, num2 := p2[0], p2[1]
        res[i] = num2
        if count2 > 1 {
            heap.Push(q, []int{count2-1, num2})
        }
        heap.Push(q, []int{count, num})
    }
    return res
}

复杂度分析

时间复杂度：$O(n\log N)$。

空间复杂度：$O(n)$，1个map的空间。