6430： 找出转圈游戏输家

题目描述

描述：n 个朋友在玩游戏。这些朋友坐成一个圈，按 顺时针方向 从 1 到 n 编号。从第 i 个朋友的位置开始顺时针移动 1 步会到达第 (i + 1) 个朋友的位置（1 <= i < n），而从第 n 个朋友的位置开始顺时针移动 1 步会回到第 1 个朋友的位置。

游戏规则如下：

第 1 个朋友接球。

接着，第 1 个朋友将球传给距离他顺时针方向 k 步的朋友。
然后，接球的朋友应该把球传给距离他顺时针方向 2 * k 步的朋友。
接着，接球的朋友应该把球传给距离他顺时针方向 3 * k 步的朋友，以此类推。
换句话说，在第 i 轮中持有球的那位朋友需要将球传递给距离他顺时针方向 i * k 步的朋友。

当某个朋友第 2 次接到球时，游戏结束。

在整场游戏中没有接到过球的朋友是 输家 。

给你参与游戏的朋友数量 n 和一个整数 k ，请按升序排列返回包含所有输家编号的数组 answer 作为答案。

输入：n = 5, k = 2
输出：[4,5]
解释：以下为游戏进行情况：
1）第 1 个朋友接球，第 1 个朋友将球传给距离他顺时针方向 2 步的玩家 —— 第 3 个朋友。
2）第 3 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 2 个朋友。
3）第 2 个朋友将球传给距离他顺时针方向 6 步的玩家 —— 第 3 个朋友。
4）第 3 个朋友接到两次球，游戏结束。

输入：n = 4, k = 4
输出：[2,3,4]
解释：以下为游戏进行情况：
1）第 1 个朋友接球，第 1 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 1 个朋友。
2）第 1 个朋友接到两次球，游戏结束。

解题思路

思路：最直观的想法是，约瑟夫环的变种。使用一个长度为n+1的visited数组存储元素是否接到过球（其中下标为0不使用），初始化均为false，表示初始均未接到过球，然后将下标为1设为true，表示第一个小朋友接到过球；使用i表示当前是第几个k，初始化为1，表示从1*k开始；使用cur表示当前小朋友编号，初始化为1，表示当前是第一个小朋友；使用nextcur表示下一个小朋友编号，初始化为(cur+i*k)%n==0?n:(cur+i*k)%n，注意此处小朋友编号从1开始而不是从0开始，故当其通过计算公式(cur+i*k)%n得到的结果是0时，其对应的应该为n（如果小朋友编号从0开始，那么对应的应该为0）；题目描述的结束条件是当某个小朋友第2次接到球，对应的代码循环结束条件即为当下一个小朋友未接到球则继续循环，在每一轮循环中，首先置访问标志，然后更新cur、i以及nextcur，循环结束后遍历visited数组，将未接到过球的小朋友编号均加入到res数组中，并返回res即可。注意，本题特殊条件如下，一是小朋友个数n=1时没有输家，二是小朋友个数n等于步长k时除了第一个小朋友均是输家。

vector<int> circularGameLosers(int n, int k) {
        vector<int> res;
        if(n==1)  //没有输家
            return res;
        if(n==k)  //除了第一个均是输家
        {
            for(int i=2;i<=n;i++)
                res.push_back(i);
            return res;
        }
        vector<bool> visited(n+1,false); //访问数组 下标为0不使用
        visited[1]=true; //第一个访问
        int i=1; //记录是第几个k
        int cur=1; //记录当前下标
        int nextcur=(cur+i*k)%n==0?n:(cur+i*k)%n; //记录下一个下标  ==0 n eg:2 1
        while(!visited[nextcur])  //下一个待访问的下标未被访问则继续
        {
            visited[nextcur]=true;
            cur=nextcur;
            i++;
            nextcur=(cur+i*k)%n==0?n:(cur+i*k)%n;
        }
        for(int i=1;i<=n;i++)
        {
            if(!visited[i])
                res.push_back(i);
        }
        return res;
    }

6431： 相邻值的按位异或

题目描述

描述：下标从 0 开始、长度为 n 的数组 derived 是由同样长度为 n 的原始 二进制数组 original 通过计算相邻值的 按位异或（⊕）派生而来。

特别地，对于范围 [0, n - 1] 内的每个下标 i ：

如果 i = n - 1 ，那么 derived[i] = original[i] ⊕ original[0]
否则 derived[i] = original[i] ⊕ original[i + 1]
给你一个数组 derived ，请判断是否存在一个能够派生得到 derived 的 有效原始二进制数组 original 。

如果存在满足要求的原始二进制数组，返回 true ；否则，返回 false 。

二进制数组是仅由 0 和 1 组成的数组。

输入：derived = [1,1,0]
输出：true
解释：能够派生得到 [1,1,0] 的有效原始二进制数组是 [0,1,0] ：
derived[0] = original[0] ⊕ original[1] = 0 ⊕ 1 = 1 
derived[1] = original[1] ⊕ original[2] = 1 ⊕ 0 = 1
derived[2] = original[2] ⊕ original[0] = 0 ⊕ 0 = 0

输入：derived = [1,1]
输出：true
解释：能够派生得到 [1,1] 的有效原始二进制数组是 [0,1] ：
derived[0] = original[0] ⊕ original[1] = 1
derived[1] = original[1] ⊕ original[0] = 1

输入：derived = [1,0]
输出：false
解释：不存在能够派生得到 [1,0] 的有效原始二进制数组。

解题思路

难度：中等。

思路：最直观的想法是，将原始二进制数组original各元素分类，即使用0和1来进行区分（此处假设同号使用0，不同号使用1），使用一个umap表示下标与符号对。遍历derived数组，如果当前元素为0，则表示原始的original[i]和original[i+1]同号，此时将umap[i+1]设置为与umap[i]相同，反之则表示原始的original[i]和original[i+1]异号，此时将umap[i+1]设置为与umap[i]相反。最后需要根据derived[n-1]判断umap[n-1]和umap[0]的关系：即如果derived[n-1]=0，则表示原始的original[n-1]和original[0]同号，即umap[n-1]应该等于umap[0]，如果不满足则不存在；同理即如果derived[n-1]=1，则表示原始的original[n-1]和original[0]异号，即umap[n-1]应该不等于umap[0]，如果不满足则不存在。（虽然可能效率不高，但是我想到了我就太厉害啦！）

bool doesValidArrayExist(vector<int>& derived) 
{
   int n=derived.size();
   // 力扣超时就去掉了这部分
   // if(n==1)  //同样长度 如果为1为false
   // {
   //     if(derived[0]==0)
   //         return true;
   //     else
   //         return false;
   // }
   // if(n==2)
   // {
   //     if(derived[0]==derived[1])
   //         return true;
   //     else
   //         return false;
   // }
   unordered_map<int,int> umap;  
   // <下标,对应分类(0/1代表符号不同)>  假设默认同号设为0 不同号设为1
   for(int i=0;i+1<n;i++) //遍历数组
   {
      if(derived[i]==0) //origin[i]和origin[i+1]同号
      {
         if(i==0) //特殊处理第一个
         {
             umap[i]=0;
             umap[i+1]=0;
         }
         else //只用处理下一个与当前的关系
         {
             umap[i+1]=umap[i];
         }
      }
      else
      {
         if(i==0) //特殊处理第一个
         {
             umap[i]=0;
             umap[i+1]=1;
         }
         else //只用处理下一个与当前的关系
         {
             umap[i+1]=(umap[i]==0)?1:0;
         }
        }
     }
     // 力扣超时就去掉了这部分
     // for(auto u:umap)
     //     cout<<u.first<<" "<<u.second<<endl;
     //判断最后一个
     if((derived[n-1]==0&&umap[n-1]==umap[0])||(derived[n-1]==1&&umap[n-1]!=umap[0]))
        return true;
     return false;
}

6433： 矩阵中移动的最大次数

题目描述

描述：给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。
返回你在矩阵中能够 移动 的 最大 次数。

示例 1：

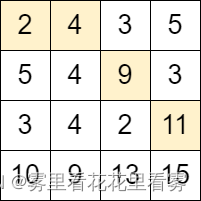
输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2：

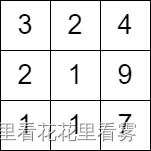
输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

解题思路

难度：中等。

思路：最直观的想法是，记忆化搜索（dfs+dp）。使用m表示矩阵行数，使用n表示矩阵列数，使用res表示结果，使用row表示当前行下标，使用col表示当前列下标，使用dp[i][j]表示从下标(i,j)出发可以移动的最大次数，使用dfs(row,col,m,n,grid,dp)表示从下标(row,col)出发可以移动的最大次数。由于是可以从第一列的任一单元格出发，故遍历行数，使用dfs获取从(i,0)出发可以移动的最大次数step，然后使用step更新res，最后返回res-1即可（因为最后一次也算作了一步）。dfs具体实现过程如下：首先判断下标row和col是否合法，如果不合法则表示无法移动，返回0即可；其次判断dp[row][col]是否已经被计算过，如果是则直接返回计算后的结果；然后使用step1、step2、step3分别收集从下标(row-1,col+1)、(row,col+1)、(row+1,col+1)出发移动的最大次数（注意因为此处需要严格比较数组元素，故需要在每次判断时对下标进行合法性判断，看起来冗余，但是非常必要），然后递推公式为dp[row][col] = max({step1,step2,step3})+1，注意，不是每次step1、step2和step3均有值，故需要初始化，最后返回dp[row][col]即可。

int dfs(int row,int col,int m,int n,vector<vector<int>>& grid,vector<vector<int>>& dp) //从(row,col)出发能移动的最大数
{
   if(row<0||col<0||row>=m||col>=n) //无法移动
     return 0;
   if(dp[row][col]!=-1)
     return dp[row][col];
   int step1=0,step2=0,step3=0;  //有的情况下step1或者step2或者step3没有
   if(grid[row-1][col+1]>grid[row][col])
       step1=dfs(row-1,col+1,m,n,grid,dp);
   if(grid[row][col+1]>grid[row][col])
       step2=dfs(row,col+1,m,n,grid,dp);
   if(grid[row+1][col+1]>grid[row][col])
       step3=dfs(row+1,col+1,m,n,grid,dp);
   dp[row][col]=max({step1,step2,step3})+1;  
   return dp[row][col];
}
int maxMoves(vector<vector<int>>& grid) 
{
    int m=grid.size();  //行
    int n=grid[0].size();  //列
    int res=0;
    vector<vector<int>> dp(m,vector<int>(n,-1));
    for(int i=0;i<m;i++)
    {
        int step=dfs(i,0,m,n,grid,dp);
        res=max(res,step);
    }
    return res-1; //最后一个算做了一次
}

6432： 统计完全连通分量的数量

题目描述

描述：给你一个整数 n 。现有一个包含 n 个顶点的 无向 图，顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [ai, bi] 表示顶点 ai 和 bi 之间存在一条 无向 边。

返回图中 完全连通分量 的数量。

如果在子图中任意两个顶点之间都存在路径，并且子图中没有任何一个顶点与子图外部的顶点共享边，则称其为 连通分量 。

如果连通分量中每对节点之间都存在一条边，则称其为 完全连通分量 。

示例 1：

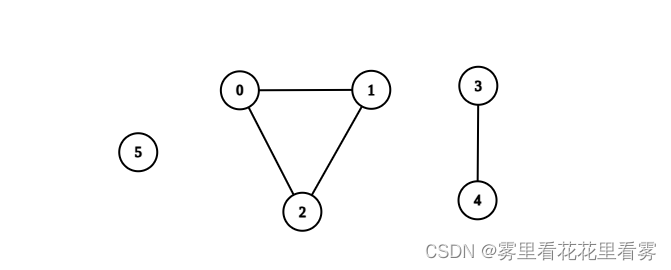
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
输出：3
解释：如上图所示，可以看到此图所有分量都是完全连通分量。

示例 2：

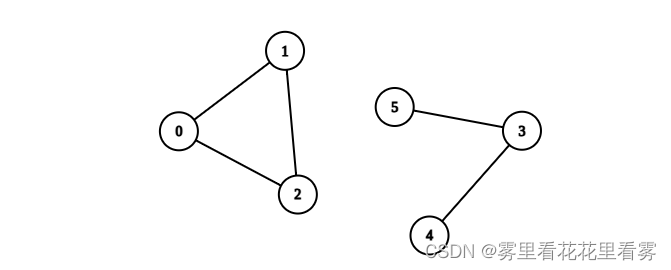
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
输出：1
解释：包含节点 0、1 和 2 的分量是完全连通分量，因为每对节点之间都存在一条边。
包含节点 3 、4 和 5 的分量不是完全连通分量，因为节点 4 和 5 之间不存在边。
因此，在图中完全连接分量的数量是 1 。

解题思路

难度：中等。

统计完全连通分量的数量：最直观的想法是，使用一个vector嵌套set的数组存储每一个点以及其对应的邻接点集合（包含自己），首先遍历结点，将结点自身加入邻接点集合中，然后遍历边，将邻接点加入邻接点集合中；接着使用一个map存储一个邻接点集合与对应的个数对，再次遍历结点，并且使用umap[m[i]]++统计邻接集合的个数；最后使用res表示完全连通分量的个数，遍历umap，取出a，b表示其pair对，其中a为set邻接点集合，b为集合个数，如果b等于a的大小，则表示是一个完全连通分量，此时将res加一，最后返回res即可。

int countCompleteComponents(int n, vector<vector<int>>& edges) 
{
	//存储每一个点以及其对应的邻接点(包含自己)
    vector<set<int>> m(n,set<int>());  
    for(int i=0;i<n;i++)
       m[i].insert(i);  //插入自己
    for(auto e:edges)
    {
       int x=e[0];
       int y=e[1];
       m[x].insert(y);  //插入邻接点
       m[y].insert(x);  //插入邻接点
    }
    //map存set unordered_map好像无法set
    map<set<int>,int> umap;   //存储一个邻接集合对应的点个数
    for(int i=0;i<n;i++)
        umap[m[i]]++;  //统计邻接集合的个数
    int res=0; //统计完全连通分量个数
    for(auto u:umap)
    {
        auto a=u.first;
        int b=u.second;
        if(a.size()==b)
          res++;
    }
    return res;
}

最后：力扣超时不一定是算法的问题，有时候有可能只是操作！