作者:@小萌新
专栏:@算法
作者简介:大二学生 希望能和大家一起进步
本篇博客简介:介绍归并排序和几道面试题
归并排序及其面试题
- 归并排序
- 归并排序是什么
- 归并排序的实际运用
- 归并排序的迭代写法
- 归并排序的时间复杂度
- 归并排序算法题
- 小和问题
- 翻转对问题
归并排序
归并排序是什么
归并排序是一种基于归并操作的有效的排序算法
它是采用分治法的一个典型的应用 将一个大的数组分成两个或多个小的数组 对每个小的数组进行排 然后再将排好序的小数组合并成一个有序的大数组
其实它的中心思想和递归差不多 ---- 分治
归并排序的实际运用
我们下面会用图解和代码的方式来详细介绍下归并排序
现在给我们一个大的无序数组

要求我们使用归并排序的思路来将这个数组进行排序
首先第一步我们要将这个数组分为左右两个部分 并且保证这个数组的左右两个部分是有序的
我们分隔之后能看到这样子的结果

但是我们发现这两个数组依然不是有序的 不满足进行合并的条件
所以说我们就要继续分割 直到有序为止
那么什么时候我们可以说一个数组是有序的呢? 当这个数组只有一个元素的时候
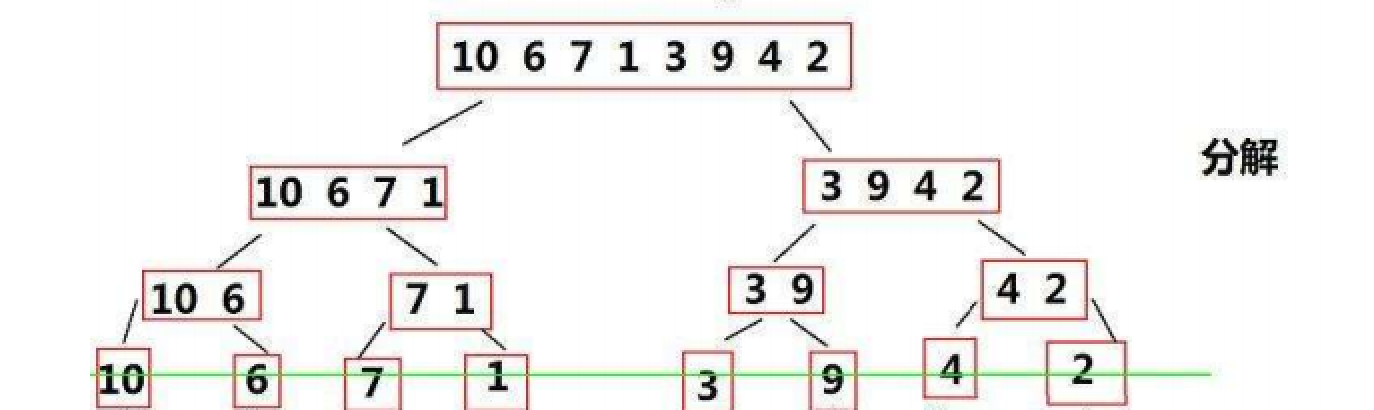
所以说该无序数组会被分隔成八个有序的数组(单个元素肯定是有序的)
之后我们开始对这八个有序的数组两两开始合并

合并成四个有序的数组之后继续开始合并

合并成两个有序的数组之后继续开始合并
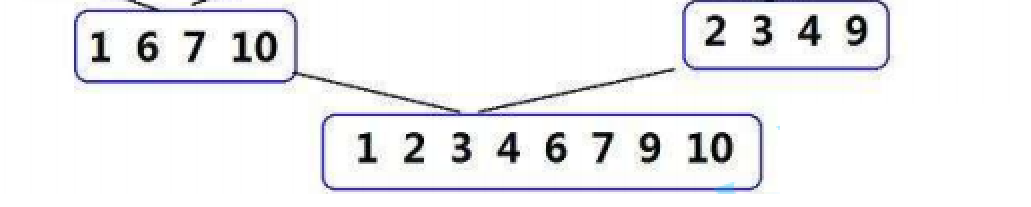
最终我们就能得到一个有序的数组了 以上就是归并排序的思路 下面我们来看代码
#include <iostream>
using namespace std;
void Merge(int arr[], int left , int mid , int right)
{
int temp[right - left + 1];
int i = left;
int j = mid + 1;
int k = 0;
while(i <= mid && j <= right)
{
if (arr[i] <= arr[j])
{
temp[k] = arr[i];
i++;
}
else
{
temp[k] = arr[j];
j++;
}
k++;
}
while(i <= mid)
{
temp[k++] = arr[i++];
}
while(j <= right)
{
temp[k++] = arr[j++];
}
for (int i = left ; i <= right ; i++)
{
arr[i] = temp[i - left];
}
}
void MergeSort(int arr[],int left , int right)
{
if (left >= right)
{
return;
}
int mid = left + (right - left) / 2;
MergeSort(arr , left , mid);
MergeSort(arr , mid+1 , right);
Merge(arr , left , mid , right);
// sorted
}
解释下上面这段代码
首先这段代码分为MergeSort和Merge两个函数
其中MergeSort函数是我们暴露给外面的接口函数 Merge函数是为了实现归并封装的一个子函数
MergeSort函数中有两次递归 这两次递归的作用是将数组两端变为有序状态 最后我们调用Merge将这两端有序的数组进行排序
我们可以写出一段代码将其验证
int main()
{
int arr[] = {10 , 6, 7, 1, 3, 9, 4, 2};
MergeSort(arr , 0 , 7);
for (int i = 0; i < 8; i++)
{
cout << arr[i] << " " ;
}
cout << endl;
return 0;
}
运行结果如下

我们可以发现运行后的结果是有序的
归并排序的迭代写法
我们可以省略递归的步骤 使用迭代的方式来写出归并排序
我们能够保证单个元素肯定是有序的 (其实递归写法最后也是从单个元素开始)
那么我们就可以将单个元素看作是一个有序的数组 直接开始归并 之后我们就能得到若干个两个元素的有序数组了 将这些两个元素的有序数组再次进行归并 我们就能得到若干个有四个元素的有序数组 依次类推
我们将两个有序数组进行归并 首先要做的就是找到这两个要进行归并的数组 前面在数量充足的时候我们可以保证没问题 但是到了后面我们可能会发现剩余的元素不能完美凑成两个相同元素的数组了
于是在我们分组的过程中会遇到一些问题
- 左数组的右边界越界了
- 右数组的左边界越界了
- 右数组的右边界越界了
至于为什么不存在左数组的左边界越界的情况 因为此时说明前面刚好排序完毕 后面不属于我们要排序的部分了
下面我们分别讨论这三种问题的解法
- 左数组的右边界越界 此时我们将剩余的部分全部纳入左数组 无需排序 因为给我们的左右数组是排好序的 如果说只存在左数组的情况就说明该段是有序的 我们就无序进行下面的操作了
- 右数组的左边界越界 此时和情况一相同 大家可以画图理解下
- 右数组的右边界越界 此时我们不管越界的部分 将右数组的右边界设置为数组末尾的位置 之后进行归并排序
代码表示如下
void MergeSort(int arr[] , int len)
{
if (len < 2)
{
return;
}
int mergesize = 1;
while(mergesize < len)
{
int L = 0;
while(L < len)
{
int M = L + mergesize -1;
if (M >= len)
{
break;
}
int R = min(len - 1 ,M + mergesize);
Merge(arr , L , M , R);
L = R + 1;
}
mergesize <<= 1;
}
}
替换递归部分的代码一共就这么多 Merge代码可以复用上面的
逻辑很简单 从数组长度为一开始(一定有序)归并 分别找出两个数组的左右边界 再考虑上前面的三种特殊情况就可以了
再每次归并完毕之后我们更新左数组的左下标
数组长度为一归并排序完毕之后我们开始归并数组长度为2的部分 (每次扩大两倍)
最后我们测试下代码运行结果
int main()
{
int arr[] = {10 , 6, 7, 1, 3, 9, 4, 2};
MergeSort(arr , 0 , 7);
for (int i = 0; i < 8; i++)
{
cout << arr[i] << " " ;
}
cout << endl;
return 0;
}
运行结果如下

归并排序的时间复杂度
归并排序的时间复杂度是N*logN 这是一个很优秀的时间复杂度
那么相比起时间复杂度为N平方的排序它优在哪里呢?
实际上它优秀的地方在于 每两个数之间只比较了一次
拿选择排序来具体 它要比较几乎整个数组才能够选择出一个最大或者最小的数 这是极其浪费的做法
我们可以利用归并排序每两个数之间只比较一次这个特性去解决很多问题
下面是一些面试算法题
归并排序算法题
小和问题
题目要求我们计算数组的小和 完整的题目和示例如下
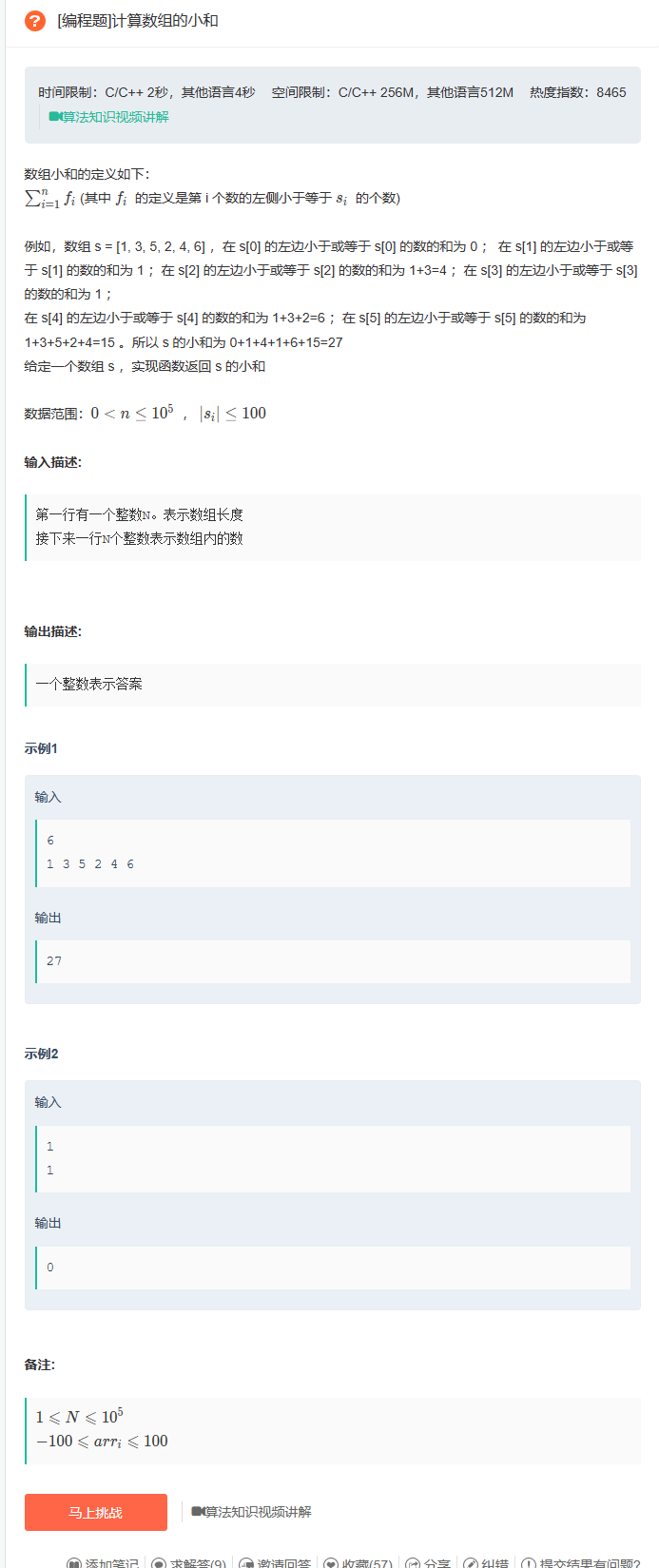
该题目出自于牛客网编程题 – 数组的小和
做这道题目最笨的方法就是多次遍历整个数组 每次找当前位置的小和 很显然这样子做的时间复杂度是N的平方 使用这种解法在面试的过程中是没有分数的!
所以我们必须要想出一个更加优秀的解法出来 实际上我们可以利用归并排序每两个数只比较一次的特点来解决
首先我们回答下下面这个问题
找出数组中所有的小和 是不是等价于将数组从左到右的比较一遍找出小于数字出现的次数啊
如果说一个数字在比较的时候小于另外一个数字 我们就叫它小于数字
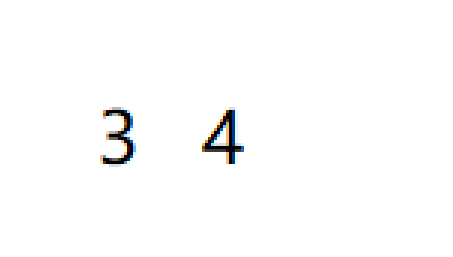
比如说数组中只有两个元素3和4 在比较的时候我们即可以说有一个数字3也可以说3出现了一次 最后得到的结果是等价的
而我们使用归并排序的过程就是这个从左到右比较的过程
代码运行如下
#include <iostream>
using namespace std;
#include <vector>
long long Merge(vector<int>& nums , int left , int mid , int right)
{
vector<int> temp(right-left+1, 0);
int i = left;
int j = mid + 1;
int k = 0;
long long SUM = 0;
while(i <= mid && j <= right)
{
if (nums[i] <= nums[j])
{
// small sum
SUM += (right - j + 1) * nums[i];
temp[k] = nums[i];
i++;
}
else
{
temp[k] = nums[j];
j++;
}
k++;
}
while(i <= mid)
{
temp[k++] = nums[i++];
}
while(j <= right)
{
temp[k++] = nums[j++];
}
for (i = left ; i <= right ; i++)
{
nums[i] = temp[i - left];
}
return SUM;
}
long long SmallNums(vector<int>& nums , int left , int right)
{
if (left >= right)
{
return 0;
}
int mid = left + (right - left) / 2;
return
SmallNums(nums, left, mid)
+
SmallNums(nums, mid + 1, right)
+
Merge(nums, left, mid, right);
}
int main()
{
long n = 0;
cin >> n;
vector<int> nums(n , 0);
for (int i = 0; i < n ; i++)
{
cin >> nums[i];
}
long long sum = SmallNums(nums, 0, n-1);
cout << sum;
return 0;
}
我们可以发现 实际上这段代码对比归并排序只多出了一行代码
- 一行代码
SUM += (right - j + 1) * nums[i];
这就是计算小和的步骤了
运行结果如下
翻转对问题
让你计算一个数组中的翻转对 题目和示例出现在lc493题
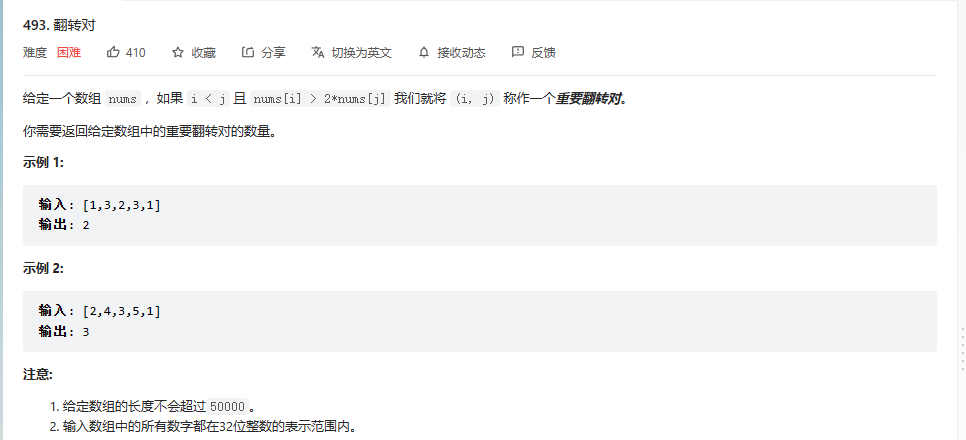
值得我们注意的是 该翻转对的下标必须要是左下标小于右下标 也就是说该翻转对必须要按照从左到右的顺序 并且只比较一遍 这里我们就应该想到使用我们的归并排序了
但是题目中的要求并不是单纯的大于小于 而是一个大于两倍的关系
这其实就是这道题目相比较于其他考查归并排序题目的一个难点 解决方案是这样子的
我们首先找出符合题目要求的数据 最后再进行归并排序
使用这个思路去解决问题就好了
也就是说归并之前我们先用一段代码来找到答案 代码表示如下
int MergeAndFind(vector<int>& nums , int left , int mid , int right)
{
int ans = 0;
int windowr = mid + 1;
for (int i = left ; i <= mid ; i++)
{
while(windowr <= right && nums[i] > (long)(nums[windowr] << 1))
{
windowr++;
}
ans += windowr - mid - 1;
}
vector<int> help(right - left + 1 , 0);
int i = left;
int j = mid + 1;
int k = 0;
while(i <= mid && j <= right)
{
if (nums[i] <= nums[j])
{
help[k] = nums[i];
i++;
}
else
{
help[k] = nums[j];
j++;
}
k++;
}
while(i <= mid)
{
help[k++] = nums[i++];
}
while (j <= right)
{
help[k++] = nums[j++];
}
for (i = left ; i <= right ; i++)
{
nums[i] = help[i - left];
}
return ans;
}
剩下的代码就是单纯的归并排序了 没有什么好讲解的 完整代码如下
class Solution {
public:
int MergeAndFind(vector<int>& nums , int left , int mid , int right)
{
int ans = 0;
int windowr = mid + 1;
for (int i = left ; i <= mid ; i++)
{
while(windowr <= right && (long long)nums[i] >((long long)nums[windowr] * 2))
{
windowr++;
}
ans += windowr - mid - 1;ii
}
vector<int> help(right - left + 1 , 0);
int i = left;
int j = mid + 1;
int k = 0;
while(i <= mid && j <= right)
{
if (nums[i] <= nums[j])
{
help[k] = nums[i];
i++;
}
else
{
help[k] = nums[j];
j++;
}
k++;
}
while(i <= mid)
{
help[k++] = nums[i++];
}
while (j <= right)
{
help[k++] = nums[j++];
}
for (i = left ; i <= right ; i++)
{
nums[i] = help[i - left];
}
return ans;
}
int _reversPairs(vector<int>& nums , int left , int right)
{
if (left >= right)
{
return 0;
}
int mid = left + (right - left) / 2;
return
_reversPairs(nums , left , mid)
+
_reversPairs(nums , mid + 1 , right)
+
MergeAndFind(nums , left , mid , right);
}
int reversePairs(vector<int>& nums)
{
return _reversPairs(nums , 0 , nums.size() -1);
}
};
这道题目注意的有两点
- 我们乘2必须要使用 “ * ” 运算符 不能使用位运算 否则负数就有可能出问题
- 在进行乘法的时候要进行类型转换 不然可能会有数据溢出的问题
以上就是归并排序的写法以及归并排序思想可以解决的一些面试题