目录
什么是图
抽象数据类型定义
常见术语
无向图
有向图
网络
邻接点
度(出度、入度)
稀疏图
稠密图、完全图
边密度
邻接矩阵表示法
用二维数组存储
用一维数组存储
邻接矩阵的好处
邻接矩阵的坏处
邻接表表示法
指针数组-链表存储
邻接表的特点
什么是图
表示“多对多”的关系
包含
抽象数据类型定义
类型名称:图(Graph)
数据对象集:G(V,E)由一个非空的有限顶点集合V和一个有限边集合E组成。
操作集:对于任意图G属于Graph,以及v属于V,e属于E
- Graph Create();建立并返回空图
- Graph InsertVertex(Graph G,Vertex v);将v插入G
- Graph InsertEdge(Graph G,Edge e);将e插入G
- void DFS(Graph G,Vertex v);从顶点v出发深度优先遍历图G
- void BFS(Graph G,Vertex v);从顶点v出发宽度优先遍历图G
- void ShortestPath(Graph G,Vertex v,int Dist[]);计算图G中顶点v到任意其他顶点的最短距离;
- void MST(Graph G);计算图G的最小生成树
- ......
常见术语
无向图
无向图是由一组节点和连接这些节点的边组成的图形结构,其中边没有方向。
有向图
有向图是由节点和有方向的边组成的图形结构。每条边都有一个指定的方向,从一个节点指向另一个节点。这意味着在有向图中,边表示了节点之间的单向关系。
网络
网络是由节点和边组成的图形结构,其中边具有权值或称为权重。
这些权值可以表示节点之间的距离、成本、容量或其他度量。
邻接点
在图中,邻接点是指与给定节点直接相连的节点。对于无向图,如果两个节点之间有一条边,则它们互为邻接点。对于有向图,只有当一条边从节点 A 指向节点 B 时,节点 B 才是节点 A 的邻接点。
度(出度、入度)
在有向图中,度是指一个节点的边的数量。
而出度是从节点出发的边的数量,表示离开该节点的连接数;
入度是指指向节点的边的数量,表示指向该节点的连接数。
稀疏图
稀疏图是指边相对较少的图。
或者说,稀疏图中节点之间的连接较少或边的数量相对较小。
稀疏图通常具有较低的边密度,节点之间的连接相对稀疏。
稠密图、完全图
稠密图是指边相对较多的图。
稠密图中节点之间的连接较多或边的数量相对较大。
稠密图具有较高的边密度,几乎每个节点都与其他节点相连。完全图是一种特殊的稠密图,其中每两个节点之间都存在一条边,也就是说,每个节点都与图中的其他节点直接相连。
边密度
对于无向图,可能的边数是 n(n-1)/2;
对于有向图,可能的边数是 n(n-1),其中 n 是节点数。
我们可以使用以下公式计算图的边密度:
d = m / (n(n-1)/2)
其中 m 是图中的边数,n 是节点数。
如果边密度接近 0,则该图被认为是稀疏图;如果边密度接近 1,则该图被认为是稠密图。
邻接矩阵表示法
用二维数组存储
邻接矩阵G[N] [N]——N个顶点从0到N-1编号

现在试着把下面这个图用邻接矩阵表示法表示出来
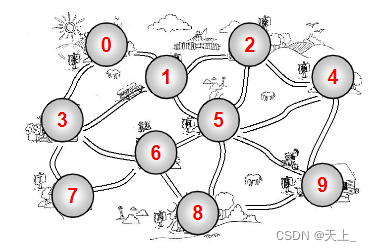
得到:
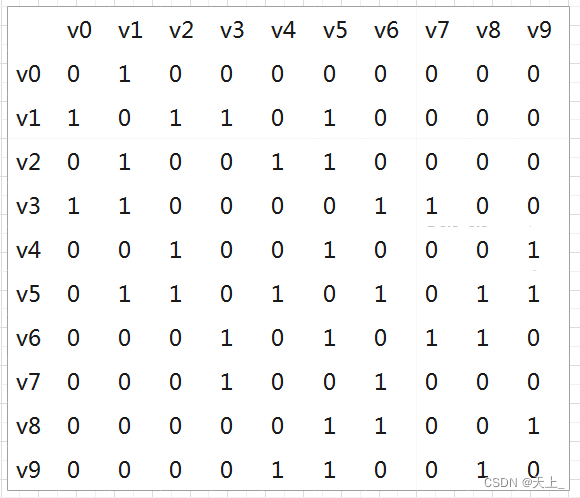
邻接矩阵的表达方式是比较简洁的,很直观地展示了节点之间的关系;
而且对于无向图来说,邻接矩阵是对称的。
用一维数组存储
对于无向图的存储,怎样可以省一半的空间?
我们利用它的对称性,就可以用一个长度为N(N+1)/2的一维数组A存储。
举个例子,假设有一个无向图,有四个节点 A、B、C、D,邻接矩阵如下:
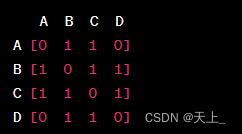
如果我们只存储对角线以上的元素,那么邻接矩阵可以表示为:

数组A为:


邻接矩阵的好处
- 直观、简单、好理解
- 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
- 方便计算任一顶点的“度”

邻接矩阵的坏处
- 浪费空间——存稀疏图有大量无效元素
对稠密图(特别是完全图)还是十分合算的
- 浪费时间——统计稀疏图中一共有多少条边
对于稀疏图而言,边的数量相对较少,很多节点之间并没有直接的连接。
因此,遍历整个邻接矩阵或邻接列表来计算边的数量将涉及大量的无效操作,导致时间和计算资源的浪费。
邻接表表示法
指针数组-链表存储
邻接表:G[N]为之指针数组,对应矩阵每行一个链表,只存非0元素
用邻接表表示法表示之前一样的图

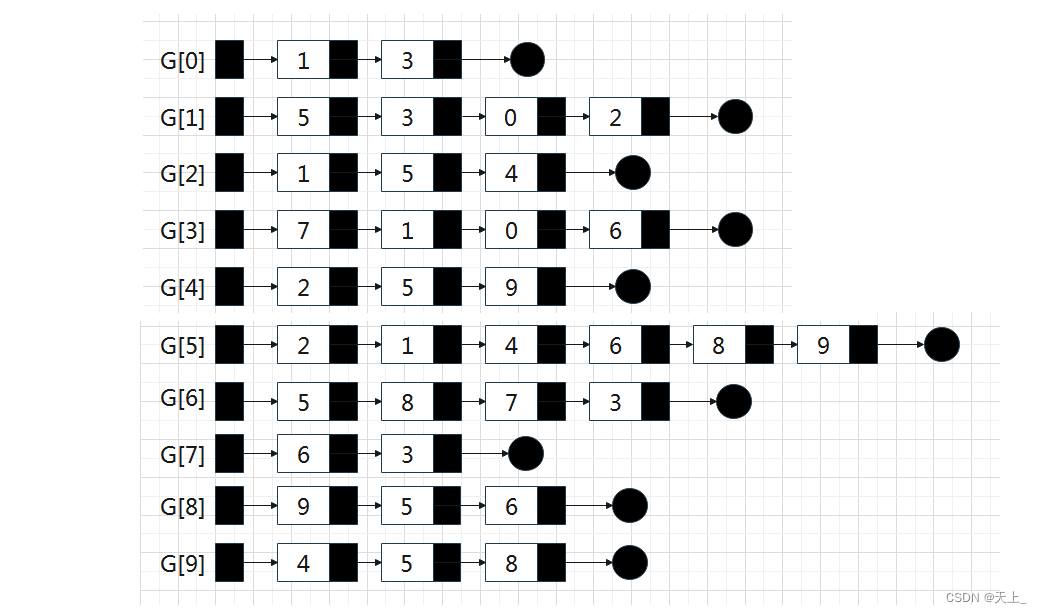
对于网络,结构中要增加权重的域。
邻接表的特点
- 方便找任一顶点的所有“邻接点”
- 节约稀疏图的空间
需要N个头指针+2E个结点(每个结点至少2个域)
- 对于无向图来说,方便计算任一顶点的“度”
而对于有向图,只能计算“出度”;需要构造“逆邻接表”(存指向自己的边)来方便计算“入度”
- 不方便检查任意一对顶点间是否存在边
end
学习自:MOOC数据结构——陈越、何钦铭