一、前言

如果机器人工程师缺乏机器人学理论的支撑和足够的认识，那么随着机器人项目的深入推进，可能会越走越艰难，所谓万丈高楼平地起，必须得打好比万丈高楼还要夯实得地基，大厦才能牢固。本篇对六轴机械臂的基础建模知识进行了较为彻底的梳理，参考了较多的网上资料，发现，很多文章或者教程并没有把DH建模这个事说得特别清楚，这里对一些注意点或者所谓的坑做了一些着重说明，仅供参考。本篇花了笔者1周的时间整理和思考，全篇的思路如下：

二、三维空间的坐标系变换

我们知道，一个直角坐标系遵照右手定则，沿着某个轴逆时针旋转θi角度的旋转矩阵为：

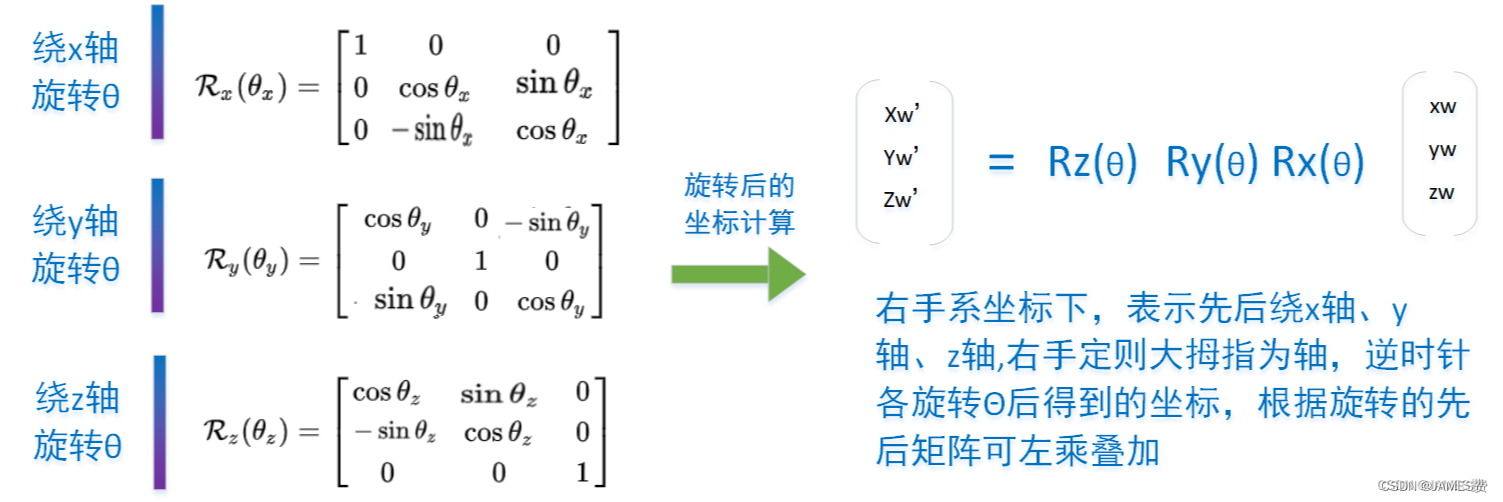
我们知道，任何一个坐标系f0，可以通过三个以上基础旋转，唯一变换到另一个同原点的坐标系fn，两个关系可以用按照变换的先后顺序左乘表示，如上图右侧。
我们知道，三维空间里，如果有两个坐标系F0，F6，如果想知道P在F6系中的向量（或者点坐标）在F0系中是多少，可以通过如下的两种形式表示：

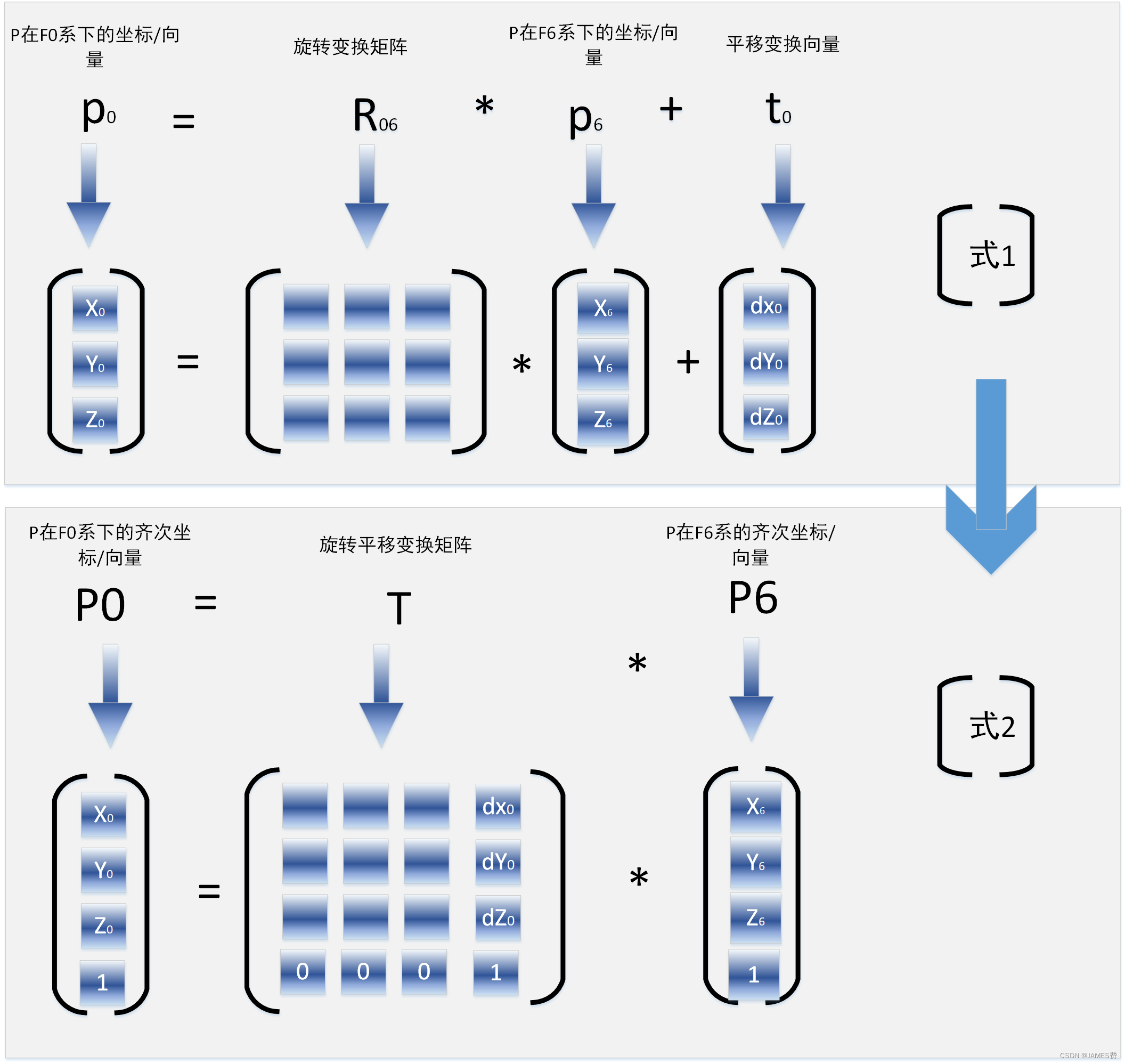
如上式2所示，旋转和平移可以组成一个齐次变换矩阵T，用在机械臂上面，可以表示一个机械臂的末端位姿：

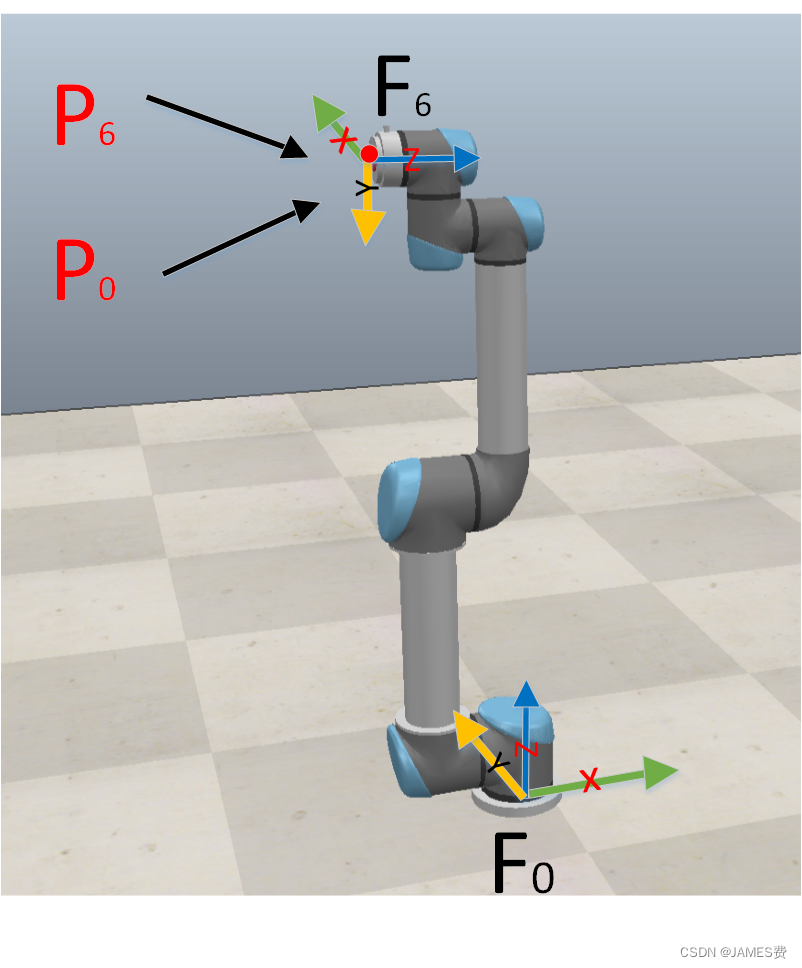
如上图，机械臂的末端位姿有两部分组成：

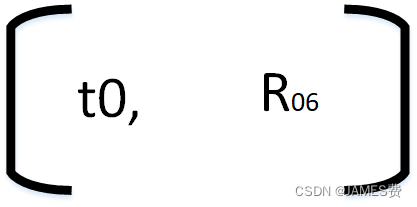
可以理解为一个是末端原点的坐标t0，一个是旋转量R06（或者可以用欧拉角序列、翻滚⾓-俯仰⾓-偏航⾓序列等表示），在图中对应的红点就是机械臂的末端的原点，其坐标其实就是t0，也就是式2中的T中的最后一列前三个（dx0，dy0，dz0）。末端的姿态还涉及到旋转，这个信息是含在了旋转矩阵R06（见式1）中。
在机械臂中，可以控制的只有各个关键的电机角度，六轴就是六个电机的角度[q1,q2,q3,q4,q5,q6]，通过设定六个电机角度，可以把机械臂的末端送到目标的位置。这个过程，数学上相当于机械臂基座的坐标系，通过一些列的旋转平移变换到了末端，由如下的这种机制：

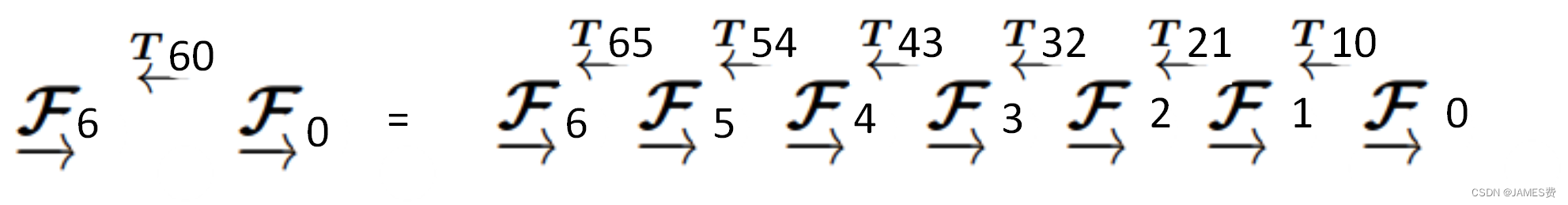
变换的矩阵T可以分解连乘得到：

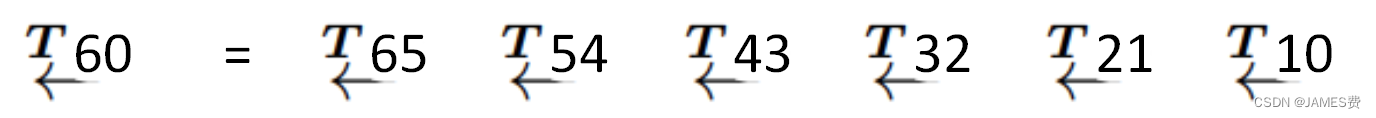
T60表示的是末端F0到F6的运动，注意到，由于变换的顺序是左乘原则，就是越左边的运动越晚，这与我们直观的感觉想违背，我们直观理解是从左往右依次进行（右乘原则），这个可以根据变换矩阵的性质，给转变过来：

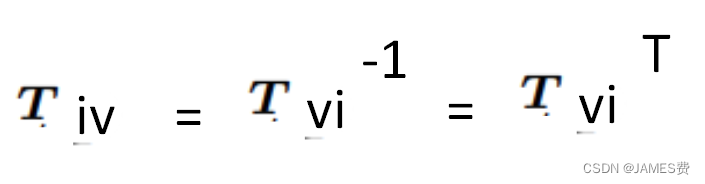
根据以上性质，可以得到右乘形式：

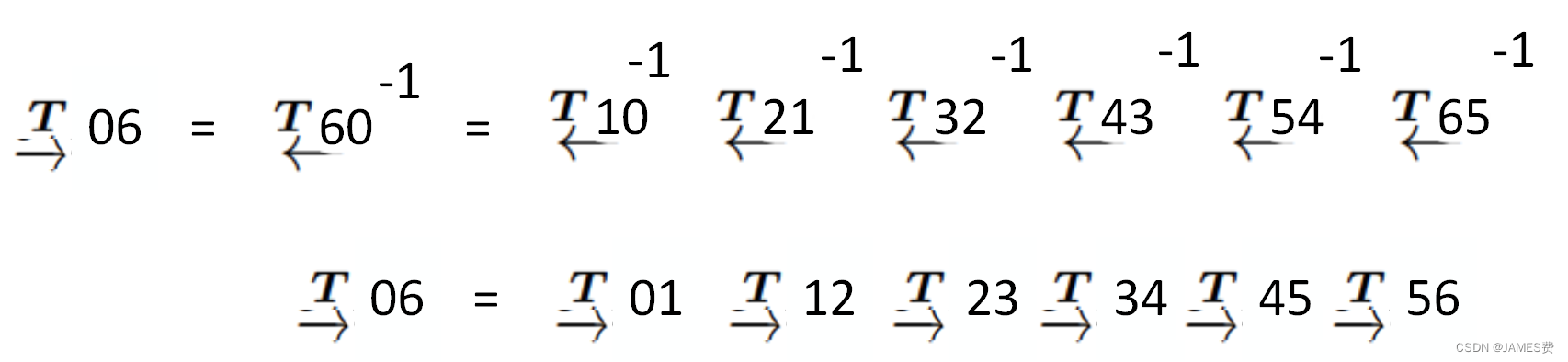
机械臂的建模就是基于类似这样的机制，有学者经过研究简化后，提出了机器人的DH建模理论。
于是，DH建模所用到的基础旋转矩阵就变为：

三、MDH建模要点

DH建模有两种，一种是标准DH建模，SDH，一种是改进DH，MDH。为了后续建模方便，建议使用MDH规则建模。其主要的原理是这样的：
（1）先确定z轴（各关节的电机转轴）：

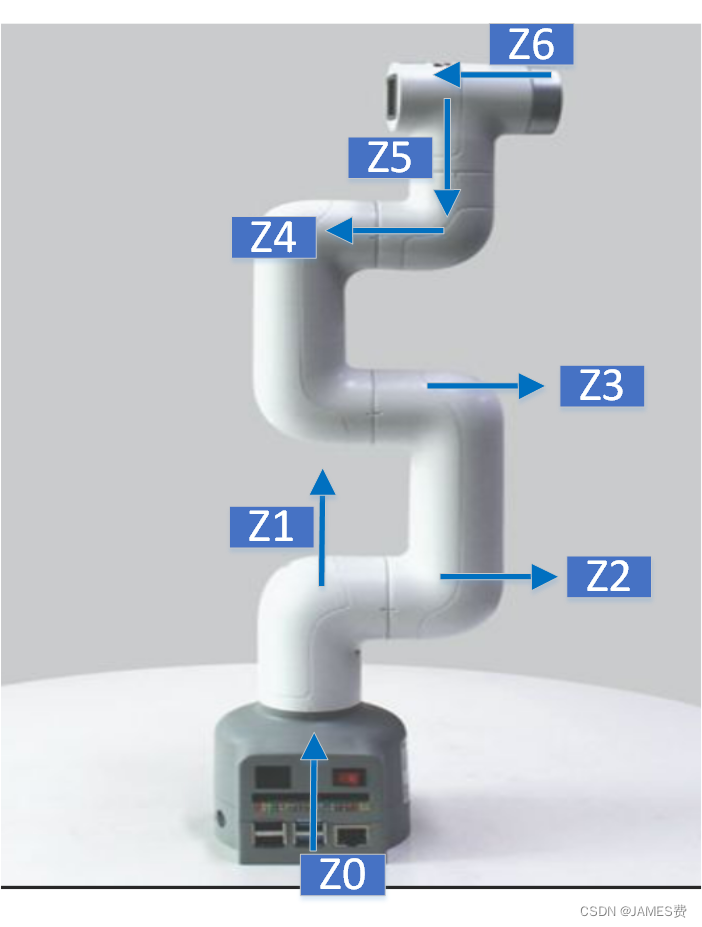
（2）逐步从固定支座base坐标系F0，确定x轴的方向，原则是x轴的要是本坐标系z轴和下一个坐标系z轴的公垂线。如上图，X0轴应该垂直于Z0，和Z1，那么可以这么定：

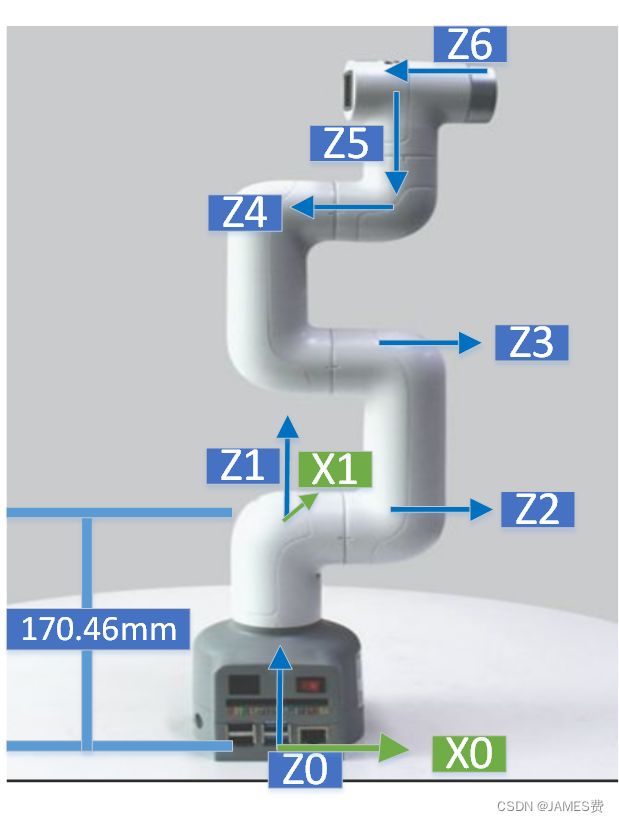
如上图，X0垂直于轴Z0和Z1，X1轴垂直于Z1和Z2，X2应该垂直于Z2和Z3…
（3）根据右乘原理，MDH中规定当前关节i的参数先后的顺序是：

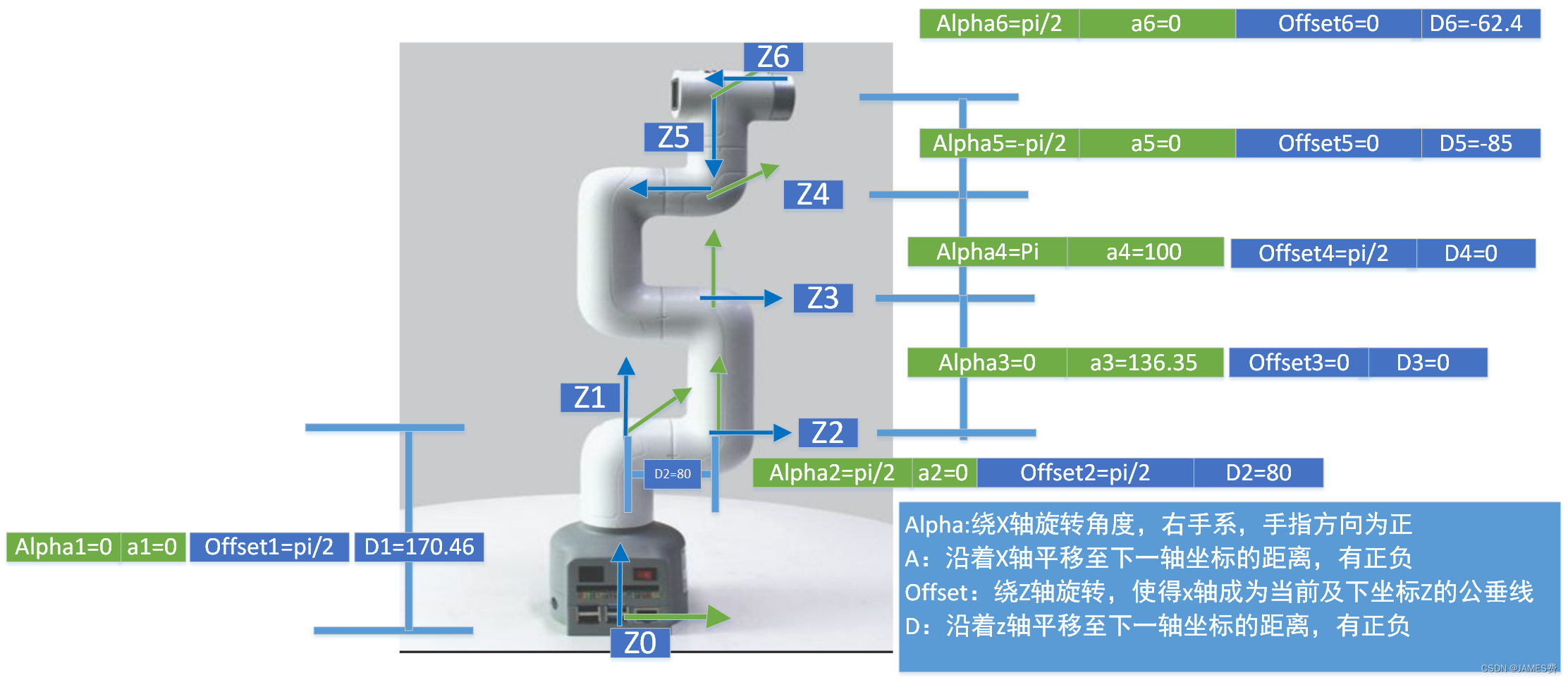
以上面的坐标系F1为例，四个参数代表是坐标F0系，先以X0轴旋转Alpha，再沿着x0轴方向移动a（负方向移动为负数），再以Z0为轴旋转Offset，最后沿着Z0方向移动d（负方向移动为负数），最后得到F1坐标系。此处，alpha1=0，X0不需要旋转，a=0，沿着X0没有平移，offset=pi/2，沿着Z0逆时针旋转90度，X0轴转到了X1轴的位置，然后d=170.56，沿着Z0正方向移动了170.56，这样经过连续的旋转+平移后，就完成了关键1的参数建模。以此类推，逐步确定其余5组参数。
所有的参数确定，如下图示例所示：

四、MDH的变换矩阵推导

根据以上的分析，MDH模型中，从一个坐标系Fi-1到Fi的变换矩阵其实可以这些推导：用python表示：

import sympy as sy

#MDH
alpha=[0,np.pi/2,0,np.pi,-np.pi/2,np.pi/2]
a=[0,0,136.35,100,0,0]
offset=[np.pi/2,np.pi/2,0,np.pi/2,0,0]
d=[170.46,80,0,0,-85,-62.4]


"""推导转换矩阵"""
#z轴旋转角度
theta1=sy.Symbol("theta1")
#z轴平移
d1=sy.Symbol("d1")

#x轴旋转角度
al1=sy.Symbol("al1")
#x轴平移

a1=sy.Symbol("a1")

def MTi(alpha,a,d,theta,DHtype="MDH"):

    #x轴旋转变化阵，右手系，逆时针为正
    Rx=sy.Matrix([
       [1, 0,        0,        0],
       [0, sy.cos(alpha), -sy.sin(alpha), 0],
       [0, sy.sin(alpha), sy.cos(alpha),  0],
       [0, 0,        0,         1]
        ])
    #沿着x轴平移，有方向
    Tx=sy.Matrix([
       [1, 0, 0,  a],
       [0, 1, 0,  0],
       [0, 0,1,   0],
       [0, 0,0,   1]
        ])
    #z轴旋转阵，右手系，逆时针为正
    Rz=sy.Matrix([
       [sy.cos(theta),  -sy.sin(theta),   0,  0],
       [sy.sin(theta), sy.cos(theta),   0,  0],
       [0,             0,            1,  0],
       [0,             0,            0,  1]
        ])
    #沿着z轴平移，有方向
    Tz=sy.Matrix([
       [1, 0, 0,  0],
       [0, 1, 0,  0],
       [0, 0,1,   d],
       [0, 0,0,   1]
        ])

    print("MDH——TR",Rx@Tx@Rz@Tz)
    #右乘原则，先旋转X轴alpha，再沿X轴平移a，再旋转Z轴theta（这里为offset值），最后沿着Z轴平移D
    return Rx@Tx@Rz@Tz
#MDH的转换矩阵如下：
MTi(al1,a1,d1,theta1)

可得到MDH的基本变换矩阵为：

简写如下：

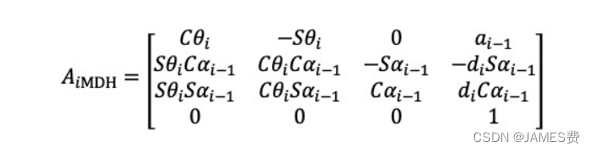
五、机械臂MDH的python模型

根据右乘原则，整个机械臂的变换矩阵，可以由6个基本变换矩阵右先后右乘获得：
A06=A1A2A2A4A5*A6
用python推导计算如下：

#MDH方法
import sympy as sy
import numpy as np
import math
from math import atan2

#MDH参数
alpha=[0,np.pi/2,0,np.pi,-np.pi/2,np.pi/2]
a=[0,0,136.35,100,0,0]
offset=[np.pi/2,np.pi/2,0,np.pi/2,0,0]
d=[170.46,80,0,0,-85,-62.4]

def MTi(alpha,a,d,theta,DHtype="MDH"):

    #x轴变化阵，右手系，顺针旋负方向
    Rx=sy.Matrix([
       [1, 0,        0,        0],
       [0, sy.cos(alpha), -sy.sin(alpha), 0],
       [0, sy.sin(alpha), sy.cos(alpha),  0],
       [0, 0,        0,         1]
        ])
    #沿着x轴平移，有方向
    Tx=sy.Matrix([
       [1, 0, 0,  a],
       [0, 1, 0,  0],
       [0, 0,1,   0],
       [0, 0,0,   1]
        ])
    #z轴旋转阵，右手系，顺针旋负方向
    Rz=sy.Matrix([
       [sy.cos(theta),  -sy.sin(theta),   0,  0],
       [sy.sin(theta), sy.cos(theta),   0,  0],
       [0,             0,            1,  0],
       [0,             0,            0,  1]
        ])
    #沿着z轴平移，有方向
    Tz=sy.Matrix([
       [1, 0, 0,  0],
       [0, 1, 0,  0],
       [0, 0,1,   d],
       [0, 0,0,   1]
        ])

    print("MDH——TR",Rx@Tx@Rz@Tz)
    return Rx@Tx@Rz@Tz

def Aiv(alpha,a,d,offset,theta=[0,0,0,0,0,0],Tnum=6):
    """
    依次右乘，推导出机械臂位姿矩阵
    """
    for i in range(Tnum):
        Ti=MTi(alpha[i],a[i],d[i],offset[i])
        if i==0:
            Ai=Ti
        else:
            Ai=Ai@Ti
    return Ai
#机械臂位姿矩阵如下
A06= Aiv(alpha,a,d,offset)  
print("位姿矩阵：",A06)

可以计算得到机械臂的位姿矩阵：

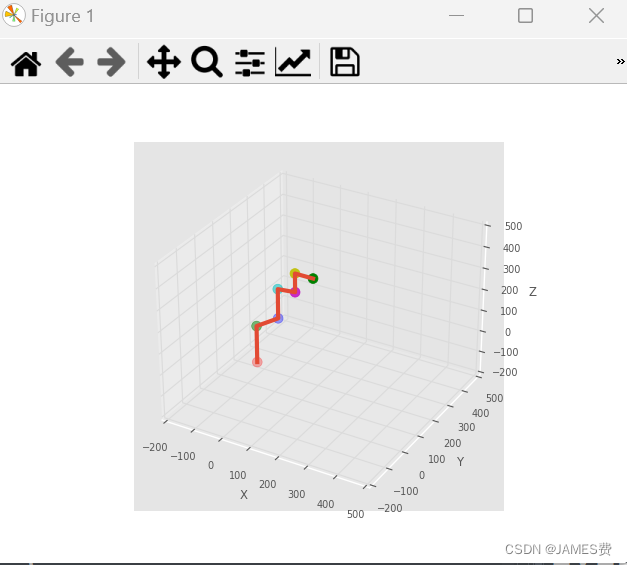
至此根据建立的MDH参数，就可以计算出末端的位姿矩阵了，为了画出机械臂的样子，我们可以通过连续变换矩阵，分别计算出各轴的位姿，并用matplot画出来：

六、python源码

可复制直接运行。
python源码资源地址