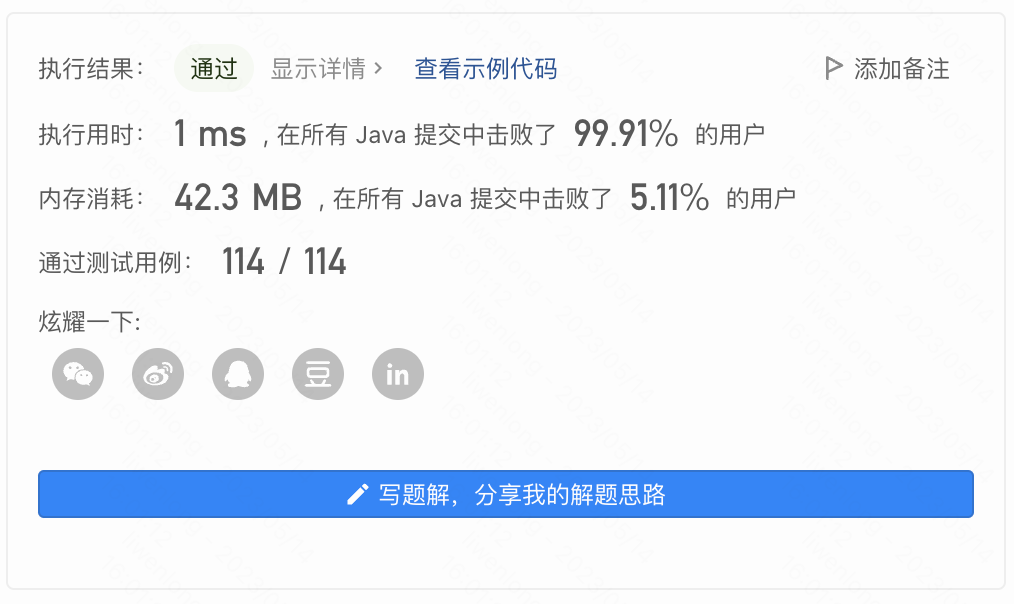
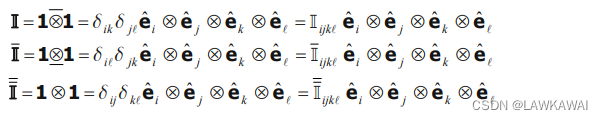题目描述

给你一棵二叉树的根节点 root ，返回树的最大宽度。

树的最大宽度是所有层中最大的宽度。

每一层的宽度被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位带符号整数范围内。

示例 1：

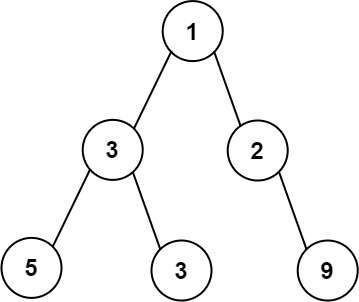
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

解题思路

第一次看到这道题的时候，求树的最大宽度，想着直接对二叉树进行层序遍历不就好了，每一层遍历开始时更新一下这一层的节点数量，这样层序遍历结束，这棵树的最大宽度也就知道了。

但是，这道题中已经说明了如果子节点为null也要计入长度，那么就需要为每个节点进行编号。其中root节点的编号为1，我们假设一个节点的编号为n，那么它的左子节点的编号一定为2*n，右子节点的编号一定为2*n+1。然后，我们根据这个规则对整个二叉树进行重新编号。

对于示例1中的二叉树，我们对其进行编号后如下图所示，每层的宽度可以使用最左侧的节点编号减去最右侧的节点编号加1，我们可以计算出每一层的宽度，最大的宽度就是4。

对于示例2中的二叉树，我们对其进行编号后如下图所示，每层的宽度可以也是使用最左侧的节点编号减去最右侧的节点编号加1，我们可以计算出每一层的宽度，最大的宽度就是7。

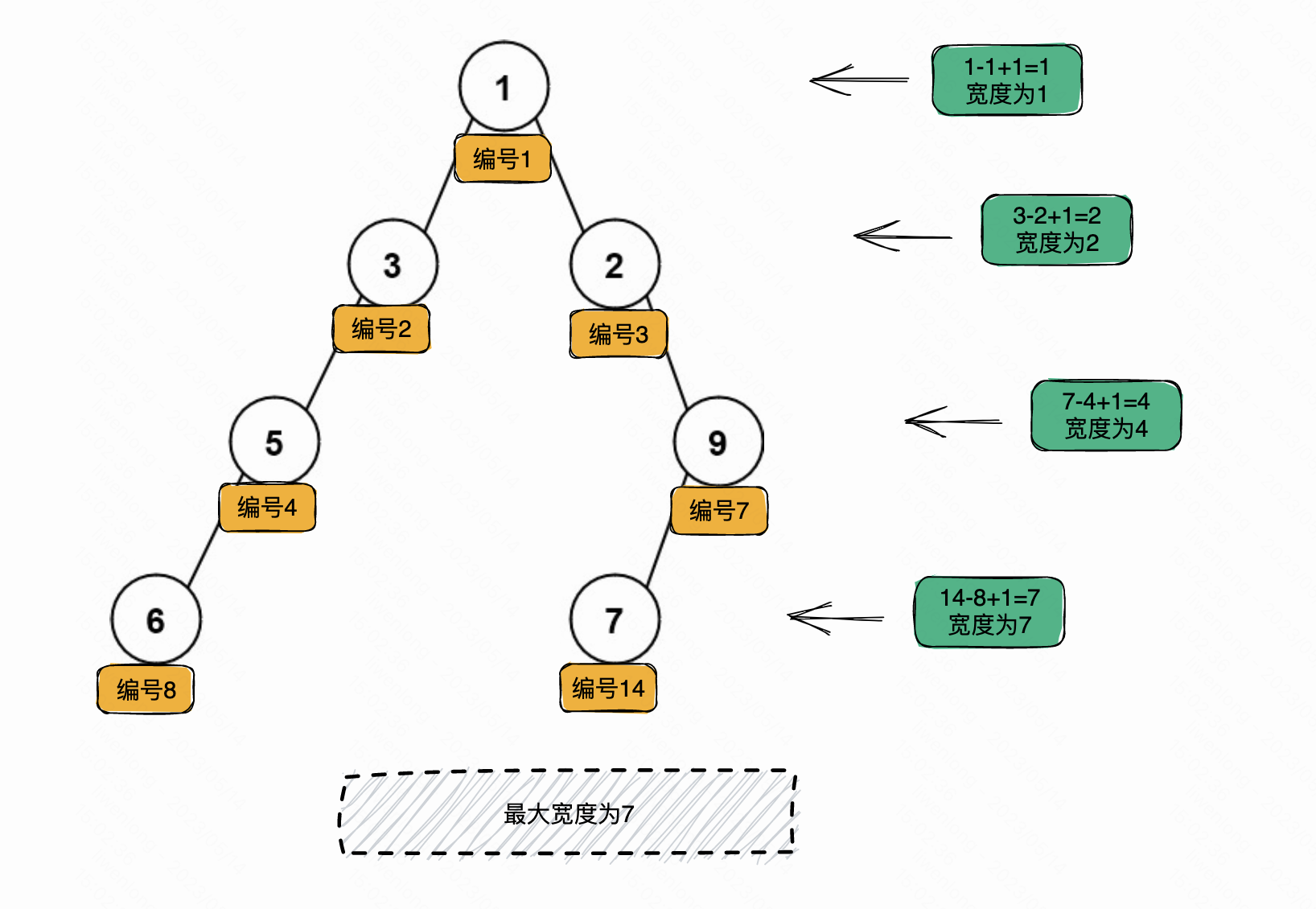接下来我们可以使用广度优先遍历和深度优先遍历两种不同的方法来求解。

解法一：广度优先遍历

我们直接套用二叉树层序遍历的思路，在遍历的过程中给每个二叉树节点进行编号，每一层遍历结束后，使用这一层最右侧节点编号减去最左侧节点编号再加1作为这一层的宽度。

lass Solution {
    public int widthOfBinaryTree(TreeNode root) {
        int res = 1;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        root.val = 1;
        while(!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            for(int i = 0; i < size; i++) {
                TreeNode curNode = queue.poll();
                list.add(curNode.val);
                if (curNode.left != null) {
                    queue.offer(curNode.left);
                    curNode.left.val = curNode.val * 2;
                }
                if (curNode.right != null) {
                    queue.offer(curNode.right);
                    curNode.right.val = curNode.val * 2 + 1;
                }
            }
            res = Math.max(res, list.get(list.size() - 1) - list.get(0) + 1);
        }
        return res;
    }
}

解法二：深度优先遍历

class Solution {
    // 存储结果
    int result = 0;
    // 存储每一层最左侧的节点编号
    Map<Integer, Integer> minValue = new HashMap();
    public int widthOfBinaryTree(TreeNode root) {
        dfs(root, 1, 0);
        return result;
    }

    /**
     * node:当前遍历到的节点
     * nodeIndex:当前节点的编号
     * level:当前节点的层数
     */
    public void dfs(TreeNode node , int nodeIndex, int level) {
        // 结束条件
        if (node == null) return;
        // 存这一层最左侧的节点编号
        minValue.putIfAbsent(level, nodeIndex);
        result = Math.max(result, nodeIndex - minValue.get(level) + 1);
        // 递归
        dfs(node.left, 2 * nodeIndex, level + 1);
        dfs(node.right, 2 * nodeIndex + 1, level + 1);
    }
}