张量的代数操作
并矢 Dyadic
两个向量的张量积是一个并矢,得到一个二阶张量
u
⃗
v
⃗
=
u
⃗
⨂
v
⃗
=
A
\vec u \vec v = \vec u \bigotimes \vec v = A
uv=u⨂v=A
其中, ⨂ \bigotimes ⨂是张量乘积,任意张量可以表示成并矢的线性组合
- ( u ⃗ ⨂ v ⃗ ) ⋅ x ⃗ = u ⃗ ( v ⃗ ⋅ x ⃗ ) ≡ u ⃗ ⨂ ( v ⃗ ⋅ x ⃗ ) ( \vec u \bigotimes \vec v ) \cdot \vec x = \vec u(\vec v \cdot \vec x) \equiv \vec u \bigotimes (\vec v \cdot \vec x) (u⨂v)⋅x=u(v⋅x)≡u⨂(v⋅x)
- u ⃗ ⨂ ( α v ⃗ + β w ⃗ ) = α u ⃗ ⨂ v ⃗ + β u ⃗ ⨂ w ⃗ \vec u \bigotimes (\alpha \vec v + \beta \vec w) = \alpha \vec u \bigotimes \vec v + \beta \vec u \bigotimes \vec w u⨂(αv+βw)=αu⨂v+βu⨂w
- ( α v ⃗ ⨂ u ⃗ + β w ⃗ ⨂ r ⃗ ) ⋅ x = α ( v ⃗ ⨂ u ⃗ ) ⋅ x + β ( w ⃗ ⨂ r ⃗ ) ⋅ x = α [ v ⃗ ⨂ ( u ⃗ ⋅ x ) ] + β [ w ⃗ ⨂ ( r ⃗ ⋅ x ⃗ ) ] (\alpha \vec v \bigotimes \vec u + \beta \vec w \bigotimes \vec r) \cdot x =\alpha(\vec v \bigotimes \vec u)\cdot x + \beta (\vec w \bigotimes \vec r) \cdot x \\ =\alpha[\vec v \bigotimes( \vec u\cdot x )]+ \beta [\vec w \bigotimes (\vec r \cdot \vec x)] (αv⨂u+βw⨂r)⋅x=α(v⨂u)⋅x+β(w⨂r)⋅x=α[v⨂(u⋅x)]+β[w⨂(r⋅x)]
并矢不满足交换律:
u
⃗
⨂
v
⃗
≠
v
⃗
⨂
u
⃗
\vec u \bigotimes \vec v \neq \vec v \bigotimes \vec u
u⨂v=v⨂u
笛卡尔坐标系表示:
A
=
u
⃗
⨂
v
⃗
=
(
u
i
e
^
i
)
⨂
(
v
j
e
^
j
)
=
u
i
v
j
(
e
^
i
⨂
e
^
j
)
=
A
i
j
e
^
i
⨂
e
^
j
A = \vec u \bigotimes \vec v = (u_i \hat e_i) \bigotimes (v_j \hat e_j)=u_i v_j (\hat e_i \bigotimes \hat e_j) = A_{ij} \hat e_i \bigotimes \hat e_j
A=u⨂v=(uie^i)⨂(vje^j)=uivj(e^i⨂e^j)=Aije^i⨂e^j
并矢的笛卡尔坐标表示:
A
=
A
i
j
e
^
i
⨂
e
^
j
\boxed{A = A_{ij}\hat e_i \bigotimes \hat e_j}
A=Aije^i⨂e^j
二阶张量的元素:
A i j = u i v j A_{ij} = u_iv_j Aij=uivj
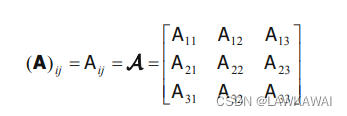
可以方便地通过张量元素的自由指标的个数来判断张量的阶数:
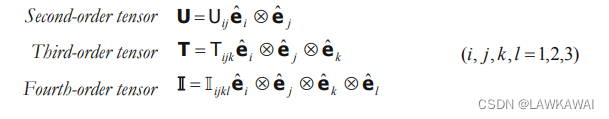
- 张量的阶数由元素的自由指标决定
- 张量的元素个数由 a n a^n an来决定,其中a是下标范围的最大值,n是自由指标的个数
问题1.12 给出张量的阶数: v i , Φ i j k , F i j k , ϵ i j , C i j k l , σ i j v_i, \Phi_{ijk}, F_{ijk}, \epsilon_{ij}, C_{ijkl}, \sigma_{ij} vi,Φijk,Fijk,ϵij,Cijkl,σij,并且给出张量 C C C的元素个数

A
,
B
A, B
A,B为二阶张量,代数操作:
-
加法: C = A + B = B + A → C i j = A i j + B i j C = A + B = B + A \rightarrow C_{ij} = A_{ij} + B_{ij} C=A+B=B+A→Cij=Aij+Bij
-
标量乘法: D = λ A → D i j = λ A i j D = \lambda A \rightarrow D_{ij} = \lambda A_{ij} D=λA→Dij=λAij
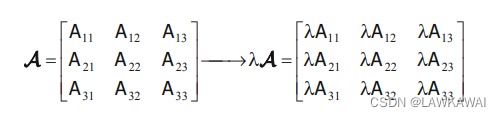
( λ A ) ⋅ v ⃗ = λ ( A ⋅ v ⃗ ) (\lambda A) \cdot \vec v = \lambda (A \cdot \vec v) (λA)⋅v=λ(A⋅v) -
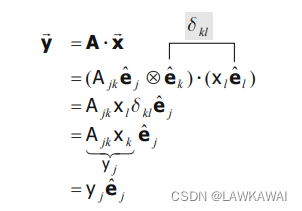
点积:
二阶张量和向量的点积得到一个一阶张量: y ⃗ = A ⋅ x ⃗ \vec y = A \cdot \vec x y=A⋅x
两个二阶张量的点积得到一个二阶张量, 但是 A ⋅ B ≠ B ⋅ A A \cdot B \neq B \cdot A A⋅B=B⋅A
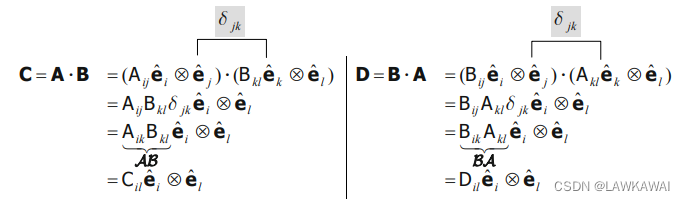
同样满足以下:
A ⋅ ( B + C ) = A ⋅ B + A ⋅ C A \cdot (B + C) = A \cdot B + A \cdot C A⋅(B+C)=A⋅B+A⋅C
A ⋅ ( B ⋅ C ) = ( A ⋅ B ) ⋅ C A \cdot (B \cdot C) = (A \cdot B) \cdot C A⋅(B⋅C)=(A⋅B)⋅C -
二阶张量的指数:
A 0 = 1 ; A 1 = A ; A 2 = A ⋅ A ; A 3 = A ⋅ A ⋅ A A^0 = 1; \quad A^1 = A; \quad A^2 = A \cdot A; \quad A^3 = A \cdot A \cdot A A0=1;A1=A;A2=A⋅A;A3=A⋅A⋅A
1是二阶单位向量
- 双标量乘积(双收缩) Double Scalar Product (Double Contraction)
考虑两个并矢: A = c ⃗ ⨂ d ⃗ , B = u ⃗ ⨂ v ⃗ A = \vec c \bigotimes \vec d, \quad B = \vec u \bigotimes \vec v A=c⨂d,B=u⨂v
双收缩(
⋅
⋅
\cdot \cdot
⋅⋅):
(
c
⃗
⨂
d
⃗
)
⋅
⋅
(
u
⃗
⨂
v
⃗
)
=
(
c
⃗
⋅
v
⃗
)
(
d
⃗
⋅
u
⃗
)
( \vec c \bigotimes \vec d) \cdot \cdot ( \vec u \bigotimes \vec v) = (\vec c \cdot \vec v)(\vec d \cdot \vec u)
(c⨂d)⋅⋅(u⨂v)=(c⋅v)(d⋅u)
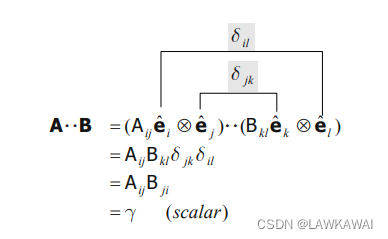
双收缩(
⋅
⋅
\cdot \cdot
⋅⋅)是可交换的:
A
⋅
⋅
B
=
B
⋅
⋅
A
A \cdot \cdot B = B \cdot \cdot A
A⋅⋅B=B⋅⋅A
双收缩( : ):
(
c
⃗
⨂
d
⃗
)
:
(
u
⃗
⨂
v
⃗
)
=
(
c
⃗
⋅
u
⃗
)
(
d
⃗
⋅
v
⃗
)
( \vec c \bigotimes \vec d) : ( \vec u \bigotimes \vec v) = (\vec c \cdot \vec u)(\vec d \cdot \vec v)
(c⨂d):(u⨂v)=(c⋅u)(d⋅v)
同样,双收缩(:)是可交换的:
B
:
A
=
(
u
⃗
⨂
v
⃗
)
:
(
c
⃗
⨂
d
⃗
)
=
(
u
⃗
⋅
c
⃗
)
(
v
⃗
⋅
d
⃗
)
=
(
c
⃗
⋅
u
⃗
)
(
d
⃗
⋅
v
⃗
)
=
A
:
B
B:A = ( \vec u \bigotimes \vec v) : ( \vec c \bigotimes \vec d) = (\vec u \cdot \vec c)(\vec v \cdot \vec d) = (\vec c \cdot \vec u)(\vec d \cdot \vec v) = A:B
B:A=(u⨂v):(c⨂d)=(u⋅c)(v⋅d)=(c⋅u)(d⋅v)=A:B
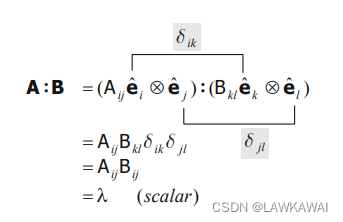
一般情况下,
A
:
B
≠
A
⋅
⋅
B
A:B \neq A \cdot \cdot B
A:B=A⋅⋅B, 但是,如果两个张量中至少有一个是对称的话,则相等:
A
s
y
m
:
B
=
A
s
y
m
⋅
⋅
B
;
A
:
B
s
y
m
=
A
⋅
⋅
B
s
y
m
;
A
s
y
m
:
B
s
y
m
=
A
s
y
m
⋅
⋅
B
s
y
m
A^{sym}:B = A^{sym}\cdot \cdot B; \quad A:B^{sym} = A\cdot \cdot B^{sym}; \\ A^{sym}: B^{sym} = A^{sym} \cdot \cdot B^{sym}
Asym:B=Asym⋅⋅B;A:Bsym=A⋅⋅Bsym;Asym:Bsym=Asym⋅⋅Bsym
三阶张量S和二阶张量B的双收缩:
结果是一个向量
S
:
B
=
(
c
⃗
⨂
d
⃗
⨂
a
)
:
(
u
⃗
⨂
v
⃗
)
=
(
a
⃗
⋅
v
⃗
)
(
d
⃗
⋅
u
⃗
)
c
⃗
B
:
S
=
(
u
⃗
⨂
v
⃗
)
:
(
c
⃗
⨂
d
⃗
⨂
a
)
=
(
u
⃗
⋅
c
⃗
)
(
v
⃗
⋅
d
⃗
)
a
⃗
S:B = ( \vec c \bigotimes \vec d \bigotimes a): ( \vec u \bigotimes \vec v)= (\vec a \cdot \vec v)(\vec d \cdot \vec u)\vec c \\ B:S = ( \vec u \bigotimes \vec v):( \vec c \bigotimes \vec d \bigotimes a)= (\vec u \cdot \vec c)(\vec v \cdot \vec d)\vec a
S:B=(c⨂d⨂a):(u⨂v)=(a⋅v)(d⋅u)cB:S=(u⨂v):(c⨂d⨂a)=(u⋅c)(v⋅d)a
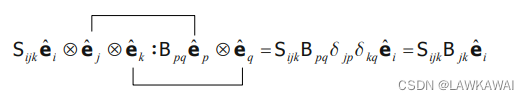
四阶张量C和二阶张量
ϵ
\epsilon
ϵ的双收缩:
应力张量和应变张量的关系:
σ
=
C
:
ϵ
\sigma = C : \epsilon
σ=C:ϵ
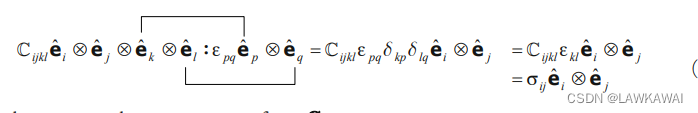
双收缩(:)的一些性质:
- A : B = B : A A:B = B:A A:B=B:A
- A : ( B + C ) = A : B + A : C A:(B+C) = A:B + A:C A:(B+C)=A:B+A:C
- λ ( A : B ) = ( λ A ) : B = A : ( λ B ) \lambda (A:B) = (\lambda A):B = A:(\lambda B) λ(A:B)=(λA):B=A:(λB)
二阶张量在笛卡尔坐标系的元素:
(
A
)
i
j
=
(
A
k
l
e
^
k
⨂
e
^
l
)
:
(
e
^
i
⨂
e
^
j
)
=
(
A
k
l
e
^
k
⋅
e
^
i
)
⨂
(
e
^
l
⋅
e
^
j
)
=
A
k
l
δ
k
i
δ
i
j
=
A
i
j
(A)_{ij} = (A_{kl} \hat e_k \bigotimes \hat e_l) : (\hat e_i \bigotimes \hat e_j) =(A_{kl} \hat e_k \cdot \hat e_i) \bigotimes (\hat e_l \cdot \hat e_j) \\ =A_{kl} \delta_{ki}\delta_{ij} = A_{ij}
(A)ij=(Akle^k⨂e^l):(e^i⨂e^j)=(Akle^k⋅e^i)⨂(e^l⋅e^j)=Aklδkiδij=Aij
可以证明:
a
⃗
⋅
A
⋅
b
⃗
=
a
p
e
^
p
⋅
A
i
j
e
^
i
⨂
e
^
j
⋅
b
r
e
^
r
=
a
p
A
i
j
b
r
δ
p
i
δ
j
r
=
a
i
A
i
j
b
j
=
A
i
j
(
a
i
b
j
)
=
A
:
(
a
⃗
⨂
b
⃗
)
\vec a \cdot A \cdot \vec b = a_p \hat e_p \cdot A_{ij} \hat e_i \bigotimes \hat e_j \cdot b_r \hat e_r =a_pA_{ij}b_r \delta_{pi} \delta_{jr} =a_i A_{ij}b_j = A_{ij}(a_ib_j)\\ = A:(\vec a \bigotimes \vec b)
a⋅A⋅b=ape^p⋅Aije^i⨂e^j⋅bre^r=apAijbrδpiδjr=aiAijbj=Aij(aibj)=A:(a⨂b)
- 向量乘积:
二阶张量和向量的乘积,利用向量的叉积: e ^ j ∧ e ^ k = ϵ i j k e ^ i \hat e_j \wedge \hat e_k = \epsilon_{ijk} \hat e_i e^j∧e^k=ϵijke^i, 有:
A ∧ x ⃗ = ( A i j e ^ i ⨂ e ^ j ) ∧ ( x k e ^ k ) = A i j x k e ^ i ⨂ ϵ l j k e ^ l = ϵ l j k A i j x k e ^ i ⨂ e ^ l A \wedge \vec x = (A_{ij} \hat e_i \bigotimes \hat e_j) \wedge (x_k \hat e_k) =A_{ij}x_k \hat e_i \bigotimes \epsilon_{ljk} \hat e_l \\ =\epsilon_{ljk}A_{ij}x_k \hat e_i \bigotimes \hat e_l A∧x=(Aije^i⨂e^j)∧(xke^k)=Aijxke^i⨂ϵljke^l=ϵljkAijxke^i⨂e^l
a
⃗
∧
(
b
⃗
∧
c
⃗
)
=
(
a
⃗
⋅
c
⃗
)
b
⃗
−
(
a
⃗
⋅
b
⃗
)
c
⃗
\vec a \wedge (\vec b \wedge \vec c) = (\vec a \cdot \vec c) \vec b - (\vec a \cdot \vec b) \vec c
a∧(b∧c)=(a⋅c)b−(a⋅b)c 的并矢表示:
[
a
⃗
∧
(
b
⃗
∧
c
⃗
)
]
j
=
(
a
k
c
k
)
b
j
−
(
a
k
b
k
)
c
j
=
(
b
j
c
k
−
b
k
c
j
)
a
k
=
[
(
b
⃗
⨂
c
⃗
−
c
⃗
⨂
b
⃗
)
⋅
a
⃗
]
j
[\vec a \wedge (\vec b \wedge \vec c) ]_j = (a_kc_k)b_j - (a_kb_k)c_j = (b_jc_k - b_kc_j)a_k =[(\vec b \bigotimes \vec c - \vec c \bigotimes \vec b) \cdot \vec a]_j
[a∧(b∧c)]j=(akck)bj−(akbk)cj=(bjck−bkcj)ak=[(b⨂c−c⨂b)⋅a]j
若
c
⃗
=
a
⃗
\vec c = \vec a
c=a,有:
[
a
⃗
∧
(
b
⃗
∧
a
⃗
)
]
j
=
(
a
k
a
k
)
b
j
−
(
a
k
b
k
)
a
j
=
(
a
k
a
k
)
b
p
δ
j
p
−
(
a
k
b
p
δ
k
p
)
a
j
=
[
(
a
k
a
k
)
δ
j
p
−
(
a
k
δ
k
p
)
a
j
]
b
p
=
[
(
a
k
a
k
)
δ
j
p
−
a
p
a
j
]
b
p
=
[
(
a
⃗
⋅
a
⃗
)
1
−
a
⃗
⨂
a
⃗
]
⋅
b
⃗
j
[\vec a \wedge (\vec b \wedge \vec a) ]_j=(a_ka_k)b_j - (a_kb_k)a_j = (a_ka_k)b_p\delta_{jp}- (a_kb_p\delta_{kp})a_j \\ =[(a_ka_k)\delta_{jp}- (a_k\delta_{kp})a_j ]b_p=[(a_ka_k)\delta_{jp}- a_pa_j ]b_p \\ = {[(\vec a \cdot \vec a)1 - \vec a \bigotimes \vec a] \cdot \vec b}_j
[a∧(b∧a)]j=(akak)bj−(akbk)aj=(akak)bpδjp−(akbpδkp)aj=[(akak)δjp−(akδkp)aj]bp=[(akak)δjp−apaj]bp=[(a⋅a)1−a⨂a]⋅bj
所以:
a
⃗
∧
(
b
⃗
∧
c
⃗
)
=
(
a
⃗
⋅
c
⃗
)
b
⃗
−
(
a
⃗
⋅
b
⃗
)
c
⃗
=
(
b
⃗
⨂
c
⃗
−
c
⃗
⨂
b
⃗
)
⋅
a
⃗
a
⃗
∧
(
b
⃗
∧
a
⃗
)
=
[
(
a
⃗
⋅
a
⃗
)
1
−
a
⃗
⨂
a
⃗
]
⋅
b
⃗
\boxed{\vec a \wedge (\vec b \wedge \vec c) = (\vec a \cdot \vec c) \vec b - (\vec a \cdot \vec b) \vec c = (\vec b \bigotimes \vec c - \vec c \bigotimes \vec b) \cdot \vec a }\\ \boxed{\vec a \wedge (\vec b \wedge \vec a) = [(\vec a \cdot \vec a)1 - \vec a \bigotimes \vec a] \cdot \vec b}
a∧(b∧c)=(a⋅c)b−(a⋅b)c=(b⨂c−c⨂b)⋅aa∧(b∧a)=[(a⋅a)1−a⨂a]⋅b
在笛卡尔坐标基中二阶张量的分量表示
一阶张量有3个分量
二阶张量有9个分量
二阶张量T在笛卡尔坐标基中的表示:
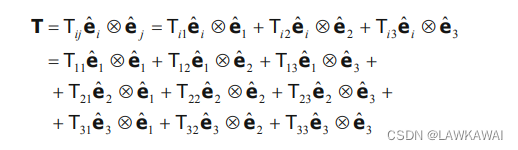
T
T
T 在
e
^
k
\hat e_k
e^k 的投影:
T
⋅
e
^
k
=
T
i
j
e
^
i
⨂
e
^
j
⋅
e
^
k
=
T
i
j
e
^
i
δ
j
k
=
T
i
k
e
^
i
=
T
1
k
e
^
1
+
T
2
k
e
^
2
+
T
3
k
e
^
3
T \cdot \hat e_k = T_{ij} \hat e_i \bigotimes \hat e_j \cdot \hat e_k =T_{ij} \hat e_i \delta_{jk} = T_{ik}\hat e_i = T_{1k}\hat e_1 +T_{2k}\hat e_2 + T_{3k}\hat e_3
T⋅e^k=Tije^i⨂e^j⋅e^k=Tije^iδjk=Tike^i=T1ke^1+T2ke^2+T3ke^3
所以,
T
T
T 在三个基的投影:
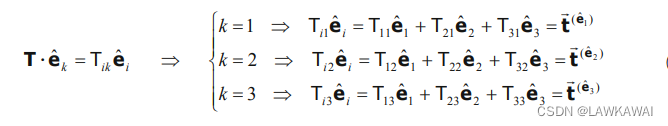
t
⃗
e
^
1
\vec t^{\hat e_1}
te^1 是
T
T
T 在
e
^
1
\hat e_1
e^1 的投影,
n
^
i
(
1
)
=
[
1
,
0
,
0
]
\hat n_i^{(1)} =[1, 0, 0]
n^i(1)=[1,0,0], 可以发现,二阶张量在一阶张量的投影得到一个一阶张量,这个一阶张量表示
T
T
T 在
e
^
i
\hat e_i
e^i 的元素分量集成
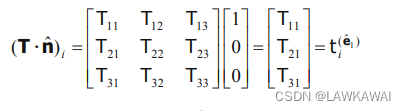
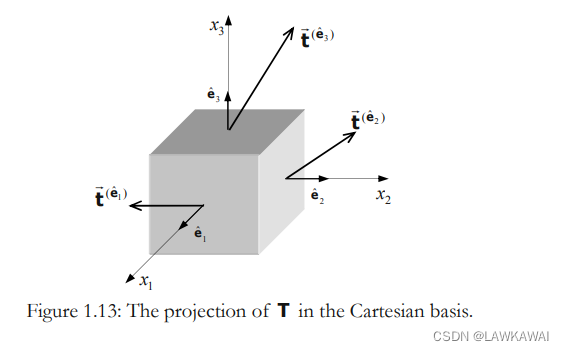
同样的,也可以写成:
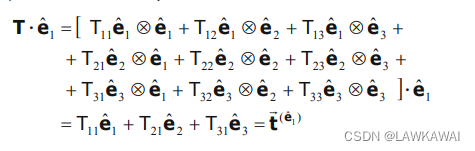
图像表示:
T
T
T 的对角线元素
(
T
11
,
T
22
,
T
33
)
(T_{11}, T_{22}, T_{33})
(T11,T22,T33) 是法向元素
T
T
T 的非对角元素
T
i
j
T_{ij}
Tij 是切向元素


张量的性质
张量的转置
A T = A j i ( e ^ i ⨂ e ^ j ) = A i j ( e ^ j ⨂ e ^ i ) A^T = A_{ji} (\hat e_i \bigotimes \hat e_j) = A_{ij} (\hat e_j \bigotimes \hat e_i) AT=Aji(e^i⨂e^j)=Aij(e^j⨂e^i)
( A T ) i j = A j i (A^T)_{ij} = A_{ji} (AT)ij=Aji
如果
A
=
u
⃗
⨂
v
⃗
A = \vec u \bigotimes \vec v
A=u⨂v, 则
A
T
=
v
⃗
⨂
u
⃗
A^T = \vec v \bigotimes \vec u
AT=v⨂u
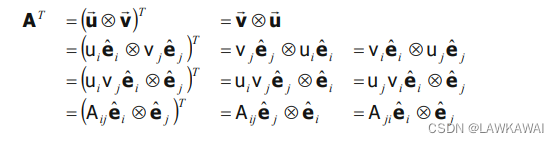
以下等式成立:
(
A
T
)
T
=
A
(A^T)^T = A
(AT)T=A
(
α
B
+
β
A
)
T
=
α
B
T
+
β
A
T
(\alpha B + \beta A)^T = \alpha B^T + \beta A^T
(αB+βA)T=αBT+βAT
(
B
⋅
A
)
T
=
A
T
⋅
B
T
(B \cdot A)^T = A^T \cdot B^T
(B⋅A)T=AT⋅BT
A
:
B
T
=
(
A
i
j
e
^
i
⨂
e
^
j
)
:
(
B
k
l
e
^
l
⨂
e
^
k
)
=
A
i
j
B
k
l
δ
i
l
δ
j
k
=
A
i
j
B
j
i
=
A
⋅
⋅
B
A:B^T = (A_{ij}\hat e_i \bigotimes \hat e_j):(B_{kl} \hat e_l \bigotimes \hat e_k) =A_{ij}B_{kl}\delta_{il}\delta_{jk} =A_{ij}B_{ji} = A \cdot \cdot B
A:BT=(Aije^i⨂e^j):(Bkle^l⨂e^k)=AijBklδilδjk=AijBji=A⋅⋅B
A
T
:
B
=
(
A
i
j
e
^
j
⨂
e
^
i
)
:
(
B
k
l
e
^
k
⨂
e
^
l
)
=
A
i
j
B
k
l
δ
j
k
δ
i
l
=
A
i
j
B
j
i
=
A
⋅
⋅
B
A^T:B = (A_{ij}\hat e_j \bigotimes \hat e_i):(B_{kl} \hat e_k\bigotimes \hat e_l) =A_{ij}B_{kl}\delta_{jk}\delta_{il} =A_{ij}B_{ji} = A \cdot \cdot B
AT:B=(Aije^j⨂e^i):(Bkle^k⨂e^l)=AijBklδjkδil=AijBji=A⋅⋅B
矩阵形式:
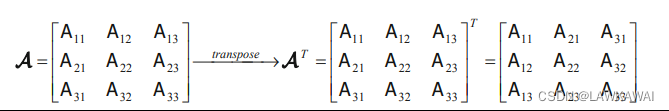
问题1.13 令A, B, C是任意张量,证明: A : ( B ⋅ C ) = ( B T ⋅ A ) : C = ( A ⋅ C T ) : B A:(B\cdot C) = (B^T \cdot A):C = (A \cdot C^T):B A:(B⋅C)=(BT⋅A):C=(A⋅CT):B

问题1.14 向量 u ⃗ , v ⃗ \vec u, \vec v u,v和二阶张量A,证明: u ⃗ ⋅ A T ⋅ v ⃗ = v ⃗ ⋅ A ⋅ u ⃗ \vec u \cdot A^T \cdot \vec v = \vec v \cdot A \cdot \vec u u⋅AT⋅v=v⋅A⋅u

对称和反对称
对称张量:
如果 A = A T A = A^T A=AT, 则 A i j = A j i A_{ij} = A_{ji} Aij=Aji, A是对称的, 记为 A ≡ A s y m A \equiv A^{sym} A≡Asym
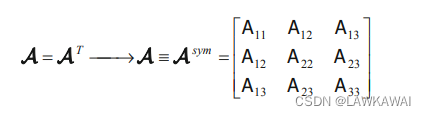
对称二阶张量只有6个独立的分量:
A
11
,
A
22
,
A
33
,
A
12
,
A
23
,
A
31
A_{11}, A_{22}, A_{33}, A_{12}, A_{23}, A_{31 }
A11,A22,A33,A12,A23,A31
根据定义,可以将对称二阶张量表示成:
A
i
j
=
A
j
i
A
i
j
+
A
i
j
=
A
j
i
+
A
i
j
2
A
i
j
=
A
j
i
+
A
i
j
A
i
j
=
1
2
(
A
j
i
+
A
i
j
)
A_{ij} = A_{ji} \\ A_{ij} + A_{ij} = A_{ji} + A_{ij} \\ 2A_{ij} = A_{ji} + A_{ij} \\ A_{ij} = \frac{1}{2}(A_{ji} + A_{ij})
Aij=AjiAij+Aij=Aji+Aij2Aij=Aji+AijAij=21(Aji+Aij)
所以, A = 1 2 ( A + A T ) A = \frac{1}{2} (A + A^T) A=21(A+AT)
对于四阶张量C,有两种对称:
Minor Symmetry:
C
i
j
k
l
=
C
j
i
k
l
=
C
i
j
l
k
=
C
j
i
l
k
C_{ijkl} = C_{jikl} = C_{ijlk} = C_{jilk}
Cijkl=Cjikl=Cijlk=Cjilk
Major Symmetry:
C
i
j
k
l
=
C
k
l
i
j
C_{ijkl} = C_{klij}
Cijkl=Cklij
没有任何对称的四阶张量有
3
4
=
81
3^4 = 81
34=81个独立的元素
对于Minor Symmetry: ij = ji,有6个独立元素;kl = lk,有6个独立元素,总共6*6 = 36个独立的元素
对于Major Symmetry: 有21个独立的元素
反对称张量:
如果
A
=
−
A
T
A = -A^T
A=−AT, 则
A
i
j
=
−
A
j
i
A_{ij} = -A_{ji}
Aij=−Aji, A是反对称的, 记为
A
≡
=
A
s
k
e
w
A \equiv = A^{skew}
A≡=Askew
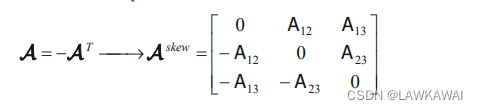
反对称张量只有3个独立分量:
A
12
,
A
23
,
A
13
A_{12}, A_{23}, A_{13}
A12,A23,A13
可以将反对称张量表示成:
A
i
j
=
−
A
j
i
A
i
j
+
A
i
j
=
−
A
j
i
+
A
i
j
2
A
i
j
=
−
A
j
i
+
A
i
j
A
i
j
=
1
2
(
−
A
j
i
+
A
i
j
)
A_{ij} = -A_{ji} \\ A_{ij} + A_{ij} = -A_{ji} + A_{ij} \\ 2A_{ij} = -A_{ji} + A_{ij} \\ A_{ij} = \frac{1}{2}(-A_{ji} + A_{ij})
Aij=−AjiAij+Aij=−Aji+Aij2Aij=−Aji+AijAij=21(−Aji+Aij)
所以, A = 1 2 ( A − A T ) A = \frac{1}{2} (A - A^T) A=21(A−AT)
考虑一个二阶反对称张量W
W
i
j
=
1
2
(
W
i
j
−
W
j
i
)
=
1
2
(
W
k
l
δ
i
k
δ
j
l
−
W
k
l
δ
j
k
δ
i
l
)
=
1
2
W
k
l
(
δ
i
k
δ
j
l
−
δ
j
k
δ
i
l
)
W_{ij} = \frac{1}{2}( W_{ij}-W_{ji}) = \frac{1}{2}( W_{kl}\delta_{ik}\delta_{jl}-W_{kl}\delta_{jk}\delta_{il}) = \frac{1}{2} W_{kl}(\delta_{ik}\delta_{jl}-\delta_{jk}\delta_{il})
Wij=21(Wij−Wji)=21(Wklδikδjl−Wklδjkδil)=21Wkl(δikδjl−δjkδil)
由于: δ i k δ j l − δ j k δ i l = δ i k δ j l − δ i l δ j k = ϵ i j r ϵ k l r \delta_{ik}\delta_{jl}-\delta_{jk}\delta_{il} =\delta_{ik}\delta_{jl}-\delta_{il}\delta_{jk}=\epsilon_{ijr}\epsilon_{klr} δikδjl−δjkδil=δikδjl−δilδjk=ϵijrϵklr
所以, W i j = 1 2 W k l ϵ i j r ϵ k l r = − 1 2 W k l ϵ i j r ϵ l k r W_{ij} = \frac{1}{2} W_{kl}\epsilon_{ijr}\epsilon_{klr} = -\frac{1}{2} W_{kl}\epsilon_{ijr}\epsilon_{lkr} Wij=21Wklϵijrϵklr=−21Wklϵijrϵlkr
其中,
W
k
l
ϵ
l
k
r
=
W
12
ϵ
21
r
+
W
13
ϵ
31
r
+
W
21
ϵ
12
r
+
W
23
ϵ
32
r
+
W
31
ϵ
13
r
+
W
32
ϵ
23
r
W_{kl}\epsilon_{lkr} = W_{12}\epsilon_{21r} + W_{13}\epsilon_{31r}+W_{21}\epsilon_{12r} + W_{23}\epsilon_{32r} + W_{31}\epsilon_{13r} + W_{32}\epsilon_{23r}
Wklϵlkr=W12ϵ21r+W13ϵ31r+W21ϵ12r+W23ϵ32r+W31ϵ13r+W32ϵ23r
假设:
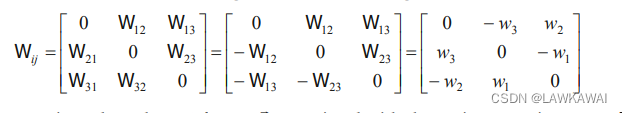
其中有,二阶反对称张量
W
W
W 的轴向量
w
⃗
\vec w
w
w
1
=
−
W
23
,
w
2
=
W
13
,
w
3
=
−
W
12
w_1 = -W_{23}, w_2 = W_{13}, w_3 = -W_{12}
w1=−W23,w2=W13,w3=−W12
w
⃗
=
w
1
e
^
1
+
w
2
e
^
2
+
w
3
e
^
3
\vec w = w_1 \hat e_1 + w_2 \hat e_2 + w_3 \hat e_3
w=w1e^1+w2e^2+w3e^3
轴向量的大小:
w
2
=
∣
∣
w
⃗
∣
∣
2
=
w
⃗
⋅
w
⃗
=
w
1
2
+
w
2
2
+
w
3
2
=
W
23
2
+
W
13
2
+
W
12
2
w^2 = ||\vec w||^2= \vec w \cdot \vec w = w_1^2 + w_2^2 +w_3^2 = W_{23}^2 + W_{13}^2+W_{12}^2
w2=∣∣w∣∣2=w⋅w=w12+w22+w32=W232+W132+W122
因此
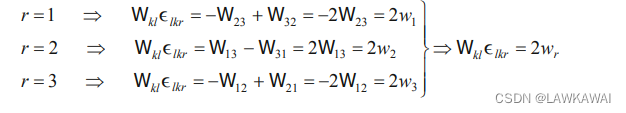
W
i
j
=
−
1
2
W
k
l
ϵ
l
k
r
ϵ
i
j
r
=
−
w
r
ϵ
r
i
j
\boxed{W_{ij} = -\frac{1}{2} W_{kl}\epsilon_{lkr}\epsilon_{ijr} =- w_r \epsilon_{rij}}
Wij=−21Wklϵlkrϵijr=−wrϵrij
乘上一个
ϵ
k
i
j
\epsilon_{kij}
ϵkij,得到:
ϵ
k
i
j
W
i
j
=
−
w
r
ϵ
r
i
j
ϵ
k
i
j
=
−
2
w
r
δ
r
k
=
−
2
w
k
\epsilon_{kij}W_{ij} =- w_r \epsilon_{rij}\epsilon_{kij} = -2w_r \delta_{rk} = -2w_k
ϵkijWij=−wrϵrijϵkij=−2wrδrk=−2wk
其中,利用了问题1.7的
ϵ
r
i
j
ϵ
k
i
j
=
2
δ
r
k
\epsilon_{rij}\epsilon_{kij} = 2\delta_{rk}
ϵrijϵkij=2δrk
所以, w k = − 1 2 ϵ k i j W i j \boxed{w_k =- \frac{1}{2}\epsilon_{kij}W_{ij}} wk=−21ϵkijWij
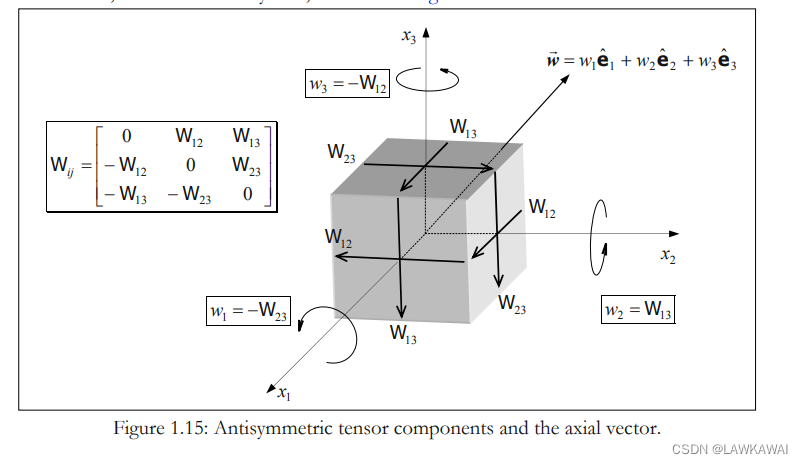
反对称张量和其对应的轴向量的图像表示:
b
⃗
⋅
W
⋅
a
⃗
=
a
⃗
⋅
W
T
⋅
b
⃗
=
−
a
⃗
⋅
W
⋅
b
⃗
\vec b \cdot W \cdot \vec a = \vec a \cdot W^T \cdot \vec b = -\vec a \cdot W \cdot \vec b
b⋅W⋅a=a⋅WT⋅b=−a⋅W⋅b
如果
a
⃗
=
b
⃗
\vec a = \vec b
a=b
a
⃗
⋅
W
⋅
a
⃗
=
W
:
(
a
⃗
⨂
a
⃗
)
=
0
\vec a \cdot W \cdot \vec a = W:(\vec a \bigotimes \vec a) = 0
a⋅W⋅a=W:(a⨂a)=0
这里的
a
⃗
⨂
a
⃗
\vec a \bigotimes \vec a
a⨂a是一个对称张量,而对称张量和反对称张量的双收缩等于0
反对称张量和向量的点积:
W
⋅
a
⃗
W\cdot \vec a
W⋅a
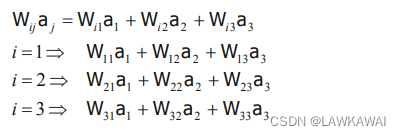
由于反对称张量的对角元素为0:
W
11
=
W
22
=
W
33
=
0
W_{11} = W_{22} =W_{33}= 0
W11=W22=W33=0,所以
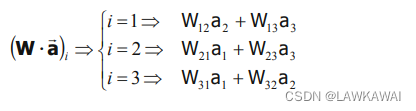
而以上结果,与
w
⃗
∧
a
⃗
\vec w \wedge \vec a
w∧a 的结果是一样的:

因此,可以将反对称张量
W
W
W 和其对应的轴向量
w
⃗
\vec w
w 联系起来:
W
⋅
a
⃗
=
w
⃗
∧
a
⃗
\boxed{W \cdot \vec a = \vec w \wedge \vec a}
W⋅a=w∧a
一个反对称张量投影到任意一个向量的结果等同于该反对称张量的轴向量与该任意向量的叉积
也可以由 W i j = − w r ϵ r i j W_{ij} =- w_r \epsilon_{rij} Wij=−wrϵrij得到
W ⋅ a ⃗ = W i k a k = − w j ϵ j i k a k = ϵ i j k w j a k = w ⃗ ∧ a ⃗ W \cdot \vec a = W_{ik}a_k = -w_j \epsilon_{jik} a_k = \epsilon_{ijk}w_ja_k=\vec w \wedge \vec a W⋅a=Wikak=−wjϵjikak=ϵijkwjak=w∧a
w ⃗ \vec w w 可以由其大小 ∣ ∣ w ⃗ ∣ ∣ = w ||\vec w|| = w ∣∣w∣∣=w 和其单位向量 e ^ i ∗ \hat e_i^* e^i∗, 有: w ⃗ = w e ^ i ∗ \vec w = w \hat e_i^* w=we^i∗
所以, W ⋅ a ⃗ = w ⃗ ∧ a ⃗ = w e ^ i ∗ ∧ a ⃗ W \cdot \vec a = \vec w \wedge \vec a = w \hat e_i^*\wedge \vec a W⋅a=w∧a=we^i∗∧a
由轴向量定义的正交基:
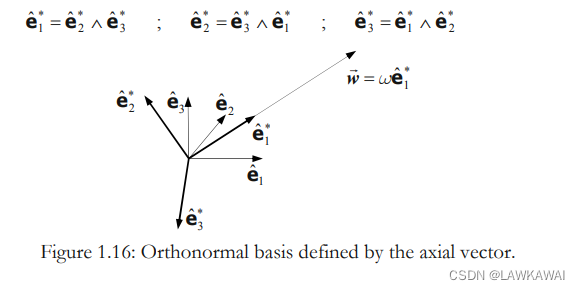
将
a
⃗
\vec a
a 表示成这个新的正交基,
a
⃗
=
a
1
e
^
1
∗
+
a
2
e
^
2
∗
+
a
3
e
^
3
∗
\vec a = a_1 \hat e_1^* + a_2 \hat e_2^* + a_3 \hat e_3^*
a=a1e^1∗+a2e^2∗+a3e^3∗, 所以
W
⋅
a
⃗
W \cdot \vec a
W⋅a
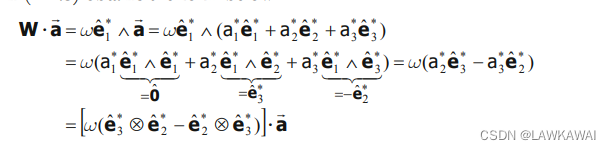
所以, 反对称张量可以表示在其轴向量构成的空间:
W
=
w
(
e
^
3
∗
⨂
e
^
2
∗
−
e
^
2
∗
⨂
e
^
3
∗
)
W = w(\hat e_3^* \bigotimes \hat e_2^* - \hat e_2^* \bigotimes \hat e_3^*)
W=w(e^3∗⨂e^2∗−e^2∗⨂e^3∗)
反对称张量在
e
^
1
∗
,
e
^
2
∗
,
e
^
3
∗
\hat e_1^*, \hat e_2^*, \hat e_3^*
e^1∗,e^2∗,e^3∗的投影:
W
⋅
e
^
1
∗
=
w
(
e
^
3
∗
⨂
e
^
2
∗
−
e
^
2
∗
⨂
e
^
3
∗
)
⋅
e
^
1
∗
=
0
⃗
W \cdot \hat e_1^* = w(\hat e_3^* \bigotimes \hat e_2^* - \hat e_2^* \bigotimes \hat e_3^*) \cdot \hat e_1^*=\vec 0
W⋅e^1∗=w(e^3∗⨂e^2∗−e^2∗⨂e^3∗)⋅e^1∗=0
W
⋅
e
^
2
∗
=
w
(
e
^
3
∗
⨂
e
^
2
∗
−
e
^
2
∗
⨂
e
^
3
∗
)
⋅
e
^
2
∗
=
w
e
^
3
∗
W \cdot \hat e_2^* = w(\hat e_3^* \bigotimes \hat e_2^* - \hat e_2^* \bigotimes \hat e_3^*) \cdot \hat e_2^*=w \hat e_3^*
W⋅e^2∗=w(e^3∗⨂e^2∗−e^2∗⨂e^3∗)⋅e^2∗=we^3∗
W
⋅
e
^
3
∗
=
w
(
e
^
3
∗
⨂
e
^
2
∗
−
e
^
2
∗
⨂
e
^
3
∗
)
⋅
e
^
3
∗
=
−
w
e
^
2
∗
W \cdot \hat e_3^* = w(\hat e_3^* \bigotimes \hat e_2^* - \hat e_2^* \bigotimes \hat e_3^*) \cdot \hat e_3^*=-w \hat e_2^*
W⋅e^3∗=w(e^3∗⨂e^2∗−e^2∗⨂e^3∗)⋅e^3∗=−we^2∗
并且,可以验证:
e
^
3
∗
⋅
W
⋅
e
^
2
∗
=
e
^
3
∗
⋅
w
⋅
e
^
3
∗
=
w
\hat e_3^* \cdot W \cdot \hat e_2^* = \hat e_3^* \cdot w \cdot \hat e_3^* = w
e^3∗⋅W⋅e^2∗=e^3∗⋅w⋅e^3∗=w
e
^
2
∗
⋅
W
⋅
e
^
3
∗
=
−
e
^
2
∗
⋅
w
⋅
e
^
2
∗
=
−
w
\hat e_2^* \cdot W \cdot \hat e_3^* =- \hat e_2^* \cdot w \cdot \hat e_2^* = -w
e^2∗⋅W⋅e^3∗=−e^2∗⋅w⋅e^2∗=−w
又因为:
e
^
k
∗
⋅
W
⋅
e
^
l
∗
=
e
^
k
∗
⋅
W
i
j
e
^
i
∗
⨂
e
^
j
∗
⋅
e
^
l
∗
=
W
i
j
δ
k
i
δ
j
l
=
W
k
l
\hat e_k^* \cdot W \cdot \hat e_l^* =\hat e_k^* \cdot W_{ij} \hat e_i^* \bigotimes \hat e_j^* \cdot \hat e_l^* =W_{ij}\delta_{ki}\delta_{jl} = W_{kl}
e^k∗⋅W⋅e^l∗=e^k∗⋅Wije^i∗⨂e^j∗⋅e^l∗=Wijδkiδjl=Wkl
所以
e
^
k
∗
⋅
W
⋅
e
^
l
∗
\hat e_k^* \cdot W \cdot \hat e_l^*
e^k∗⋅W⋅e^l∗ 表示取二阶张量W的kl元素, 所以,反对称二阶张量在其轴向量
w
⃗
\vec w
w 构成的正交基
e
1
∗
,
e
2
∗
,
e
3
∗
e_1^*, e_2^*, e_3^*
e1∗,e2∗,e3∗ 的元素下标只要有1,就全部为0,矩阵表示如下:
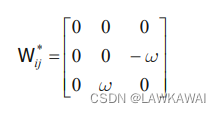
W
23
=
−
w
,
W
32
=
w
W_{23} = -w, \quad W_{32} = w
W23=−w,W32=w, 说明在新的坐标系下,反对称张量W的分量分布如下:

反对称张量W在其轴向量构成的坐标系下的分量绕着轴向量
w
⃗
\vec w
w 的方向
e
^
1
∗
\hat e_1^*
e^1∗
W
23
W_{23}
W23表示在以
e
^
3
∗
\hat e_3^*
e^3∗ 为法向的平面, 张量在
e
^
2
∗
\hat e_2^*
e^2∗ 的分量, 其值为-w,说明是跟
e
^
2
∗
\hat e_2^*
e^2∗ 方向相反;
W
32
W_{32}
W32表示在以
e
^
2
∗
\hat e_2^*
e^2∗ 为法向的平面, 张量在
e
^
3
∗
\hat e_3^*
e^3∗ 的分量, 其值为w,跟
e
^
3
∗
\hat e_3^*
e^3∗ 方向一致;
和分解:对称和反对称部分 Additive Decomposition:
将二阶张量分解成对称张量和反对称张量
A
=
1
2
(
A
+
A
T
)
+
1
2
(
A
−
A
T
)
=
A
s
y
m
+
A
s
k
e
w
A = \frac{1}{2}(A + A^T) +\frac{1}{2}(A - A^T) =A^{sym} + A^{skew}
A=21(A+AT)+21(A−AT)=Asym+Askew
对于任意的两个二阶张量:
(
A
T
⋅
B
⋅
A
)
s
y
m
=
1
2
[
(
A
T
⋅
B
⋅
A
)
+
(
A
T
⋅
B
⋅
A
)
T
]
=
1
2
[
(
A
T
⋅
B
⋅
A
)
+
(
A
T
⋅
B
T
⋅
A
)
]
=
A
T
⋅
1
2
[
B
+
B
T
]
⋅
A
=
=
A
T
⋅
B
s
y
m
⋅
A
(A^T \cdot B \cdot A)^{sym}=\frac{1}{2}[(A^T \cdot B \cdot A) + (A^T \cdot B \cdot A)^T]\\=\frac{1}{2}[(A^T \cdot B \cdot A) + (A^T \cdot B^T \cdot A)] \\ =A^T \cdot \frac{1}{2}[B + B^T ]\cdot A \\==A^T \cdot B^{sym}\cdot A
(AT⋅B⋅A)sym=21[(AT⋅B⋅A)+(AT⋅B⋅A)T]=21[(AT⋅B⋅A)+(AT⋅BT⋅A)]=AT⋅21[B+BT]⋅A==AT⋅Bsym⋅A
问题1.15 证明当 σ \sigma σ 一个对称二阶张量以及 W W W 是反对称张量时, σ : W = 0 \sigma : W = 0 σ:W=0总是成立

问题1.16 证明:a) M ⃗ ⋅ Q ⋅ M ⃗ = M ⃗ ⋅ Q s y m ⋅ M ⃗ \vec M \cdot Q \cdot \vec M =\vec M \cdot Q^{sym} \cdot \vec M M⋅Q⋅M=M⋅Qsym⋅M; b) A : B = A s y m : B s y m + A s k e w : B s k e w A:B = A^{sym}:B^{sym} + A^{skew}:B^{skew} A:B=Asym:Bsym+Askew:Bskew

其中,
a)的证明用到反对称张量:
a
⃗
⋅
W
⋅
a
⃗
=
a
⃗
⋅
w
⃗
∧
a
⃗
=
0
\vec a \cdot W \cdot \vec a = \vec a \cdot \vec w \wedge \vec a = 0
a⋅W⋅a=a⋅w∧a=0
b)的证明用到:
A
s
y
m
:
B
s
k
e
w
=
(
A
i
j
e
^
j
⨂
e
^
i
)
:
(
−
B
k
l
)
e
^
l
⨂
e
^
k
=
−
A
i
j
B
k
l
δ
j
l
δ
i
k
=
−
A
i
j
B
i
j
=
0
A^{sym}:B^{skew} = (A_{ij} \hat e_j \bigotimes \hat e_i):(-B_{kl})\hat e_l\bigotimes \hat e_k =-A_{ij}B_{kl}\delta_{jl} \delta_{ik} = -A_{ij}B_{ij}=0
Asym:Bskew=(Aije^j⨂e^i):(−Bkl)e^l⨂e^k=−AijBklδjlδik=−AijBij=0
A
s
k
e
w
:
B
s
y
m
=
(
−
A
i
j
e
^
j
⨂
e
^
i
)
:
(
B
k
l
)
e
^
l
⨂
e
^
k
=
−
A
i
j
B
k
l
δ
j
l
δ
i
k
=
−
A
i
j
B
i
j
=
0
A^{skew}:B^{sym} = (-A_{ij} \hat e_j \bigotimes \hat e_i):(B_{kl})\hat e_l\bigotimes \hat e_k =-A_{ij}B_{kl}\delta_{jl} \delta_{ik} = -A_{ij}B_{ij}=0
Askew:Bsym=(−Aije^j⨂e^i):(Bkl)e^l⨂e^k=−AijBklδjlδik=−AijBij=0
问题1.17 T T T是二阶张量, n ⃗ \vec n n是向量,验证 T ⋅ n ⃗ = n ⃗ ⋅ T T \cdot \vec n = \vec n \cdot T T⋅n=n⋅T是否成立


问题1.18 计算反对称张量 ( x ⃗ ⨂ a ⃗ ) s k e w (\vec x \bigotimes \vec a)^{skew} (x⨂a)skew所关联的轴向量 w ⃗ \vec w w

利用了
a
⃗
∧
(
b
⃗
∧
c
⃗
)
=
(
a
⃗
⋅
c
⃗
)
b
⃗
−
(
a
⃗
⋅
b
⃗
)
c
⃗
=
(
b
⃗
⨂
c
⃗
−
c
⃗
⨂
b
⃗
)
⋅
a
⃗
\vec a \wedge (\vec b \wedge \vec c) = (\vec a \cdot \vec c) \vec b - (\vec a \cdot \vec b) \vec c = (\vec b \bigotimes \vec c - \vec c \bigotimes \vec b) \cdot \vec a
a∧(b∧c)=(a⋅c)b−(a⋅b)c=(b⨂c−c⨂b)⋅a, 有:
(
x
⃗
⨂
a
⃗
−
a
⃗
⨂
x
⃗
)
⋅
z
⃗
=
z
⃗
∧
(
x
⃗
∧
a
⃗
)
(\vec x \bigotimes \vec a - \vec a \bigotimes \vec x) \cdot \vec z = \vec z \wedge (\vec x \wedge \vec a)
(x⨂a−a⨂x)⋅z=z∧(x∧a)
Cofactor Tensor & Adjugate of a Tensor
一种特殊的张量
c
o
f
(
A
)
cof(A)
cof(A)
c
o
f
(
A
)
⋅
(
a
⃗
∧
b
⃗
)
=
(
A
⋅
a
⃗
)
∧
(
A
⋅
b
⃗
)
cof(A) \cdot (\vec a \wedge \vec b) = (A \cdot \vec a) \wedge(A\cdot \vec b)
cof(A)⋅(a∧b)=(A⋅a)∧(A⋅b)
定义 adjugate of A:
a
d
j
(
A
)
=
[
c
o
f
(
A
)
]
T
adj(A) = [cof(A)]^T
adj(A)=[cof(A)]T
满足以下条件:
[
a
d
j
(
A
)
]
T
=
a
d
j
(
A
T
)
[adj(A)]^T = adj(A^T)
[adj(A)]T=adj(AT)
由前面
c
o
f
(
A
)
cof(A)
cof(A)的定义,写出指标形式:
[
c
o
f
(
A
)
i
t
ϵ
t
p
r
a
p
b
r
]
=
ϵ
i
j
k
A
j
p
a
p
A
k
r
b
r
=
(
ϵ
i
j
k
A
j
p
A
k
r
)
a
p
b
r
[cof(A)_{it}\epsilon_{tpr}a_pb_r] = \epsilon_{ijk}A_{jp}a_pA_{kr}b_r=(\epsilon_{ijk}A_{jp}A_{kr})a_pb_r
[cof(A)itϵtprapbr]=ϵijkAjpapAkrbr=(ϵijkAjpAkr)apbr
所以,有:
[
c
o
f
(
A
)
i
t
ϵ
t
p
r
=
ϵ
i
j
k
A
j
p
A
k
r
[cof(A)_{it}\epsilon_{tpr} = \epsilon_{ijk}A_{jp}A_{kr}
[cof(A)itϵtpr=ϵijkAjpAkr
在两侧同乘以
ϵ
q
p
r
\epsilon_{qpr}
ϵqpr, 有:
[
c
o
f
(
A
)
i
t
ϵ
t
p
r
ϵ
q
p
r
=
ϵ
i
j
k
ϵ
q
p
r
A
j
p
A
k
r
[cof(A)_{it}\epsilon_{tpr}\epsilon_{qpr} = \epsilon_{ijk}\epsilon_{qpr} A_{jp}A_{kr}
[cof(A)itϵtprϵqpr=ϵijkϵqprAjpAkr
[
c
o
f
(
A
)
i
t
2
δ
t
q
=
ϵ
i
j
k
ϵ
q
p
r
A
j
p
A
k
r
[cof(A)_{it}2\delta_{tq} = \epsilon_{ijk}\epsilon_{qpr} A_{jp}A_{kr}
[cof(A)it2δtq=ϵijkϵqprAjpAkr
[
c
o
f
(
A
)
i
q
=
1
2
ϵ
i
j
k
ϵ
q
p
r
A
j
p
A
k
r
[cof(A)_{iq}=\frac{1}{2} \epsilon_{ijk}\epsilon_{qpr} A_{jp}A_{kr}
[cof(A)iq=21ϵijkϵqprAjpAkr








![[LeetCode周赛复盘] 第 104 场双周赛20230513](https://img-blog.csdnimg.cn/096f183d4da44bd693fdf7823c5c17ba.png)