本篇博客会讲解力扣“141. 环形链表”的解题思路，这是题目链接。

审题

先来审题：

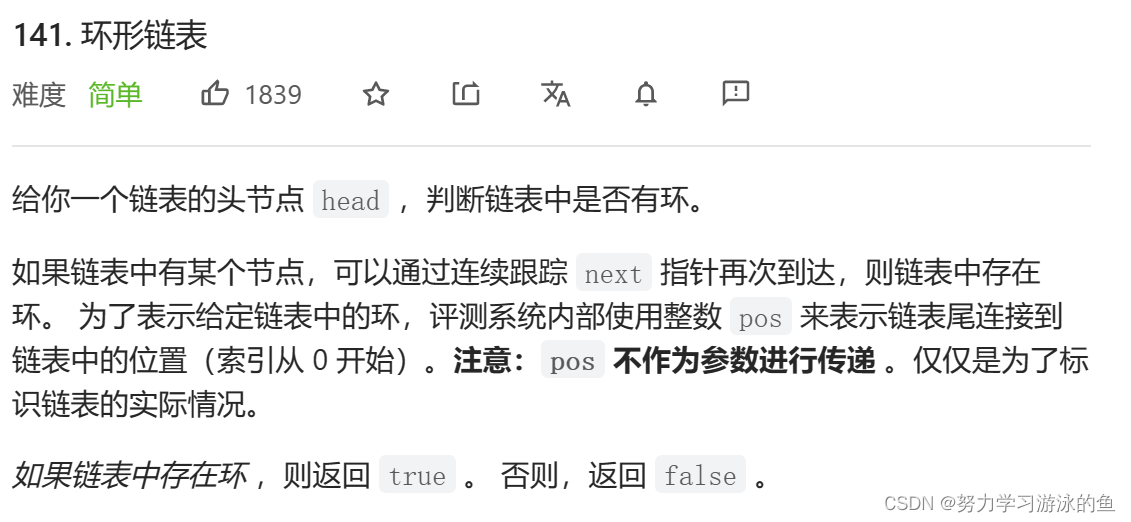
以下是输出示例：

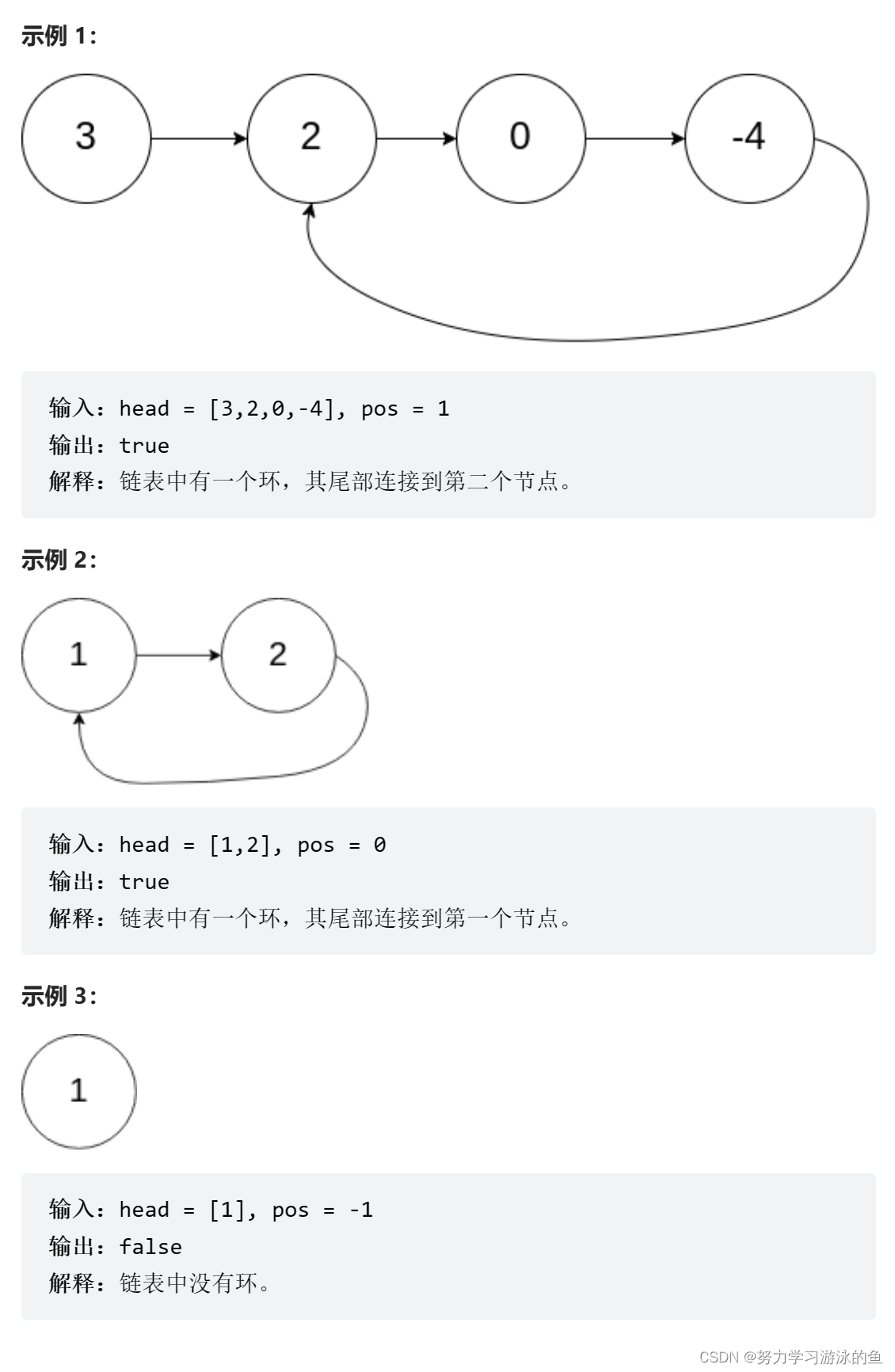
以下是提示：

以下是进阶：

思路

本题有一种非常巧妙的解法：快慢指针法，又称龟兔赛跑法。思路如下：

定义一个快指针，从头结点开始，每次走2步；定义一个慢指针，从头结点开始，每次走1步。接下来分2种情况：

1. 没有环：快指针会跑在前面，率先走到链表尾部。
2. 有环：快慢指针先后进环，在环里跑圈，快指针会追上慢指针。

代码

我先写代码，再来证明以上说法的合理性。

bool hasCycle(struct ListNode *head) {
    // 定义快慢指针
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    // 龟兔赛跑
    while (fast && fast->next)
    {
        // slow一次走1步
        slow = slow->next;
        // fast一次走2步
        fast = fast->next->next;
        // 若fast追上了slow，说明有环
        if (slow == fast)
            return true;
    }

    // fast走到了链表尾，说明没有环
    return false;
}

轻松通过。

证明

接下来有2个问题：

1. 当链表中存在环时，为什么快指针一次走2步，慢指针一次走1步，快指针一定会追上慢指针？
2. 如果快指针一次走3步，慢指针一次走1步，快指针是否一定能追上慢指针呢？

先来回答第一个问题。我们来模拟以下过程：假设链表中存在环，快指针会先进环，慢指针会后进环，接着快指针开始追击慢指针。

假设快指针和慢指针之间差了n个结点，由于每次追击，快指针都会比慢指针多走1步，每次距离会缩小1，它们之间的距离就会如下变化：

n
n-1
n-2
...
3
2
1
0

当距离减到0时，快指针就追上了慢指针。由于每次距离都会缩小1，2个指针不会错过，一定能追上。

接着回答第二个问题：还是假设链表有环，快指针先进环，慢指针后进环，开始追击。假设此时快慢指针的距离为n，每次追击，快指针会比慢指针多走2步，它们之间的距离变化就是：

n
n-2
n-4
...

此时就分为2种情况，n为偶数时：

n
n-2
n-4
...
4
2
0

2个指针的距离会缩小到0，能够追上。但是若n为奇数呢？

n
n-2
n-4
...
5
3
1
-1
...

这个-1代表了，快指针错过了慢指针，跑到慢指针前面了。假设环的长度是c，那么此时快慢指针的距离就是c-1。此时又分2种情况，若c-1为偶数，那么就能够追上；若c-1为奇数，又会错过，距离变成-1，看做c-1，而c-1还是奇数，周而复始，每次都会错过，就永远追不上了。

所以，若快指针一次走3步，慢指针一次走1步，若链表中存在环，当快慢指针都进环时的距离为n，环的周长为c时，分为3种情况：

1. n为偶数，能够追上。
2. n为奇数，但c-1为偶数，能够追上。
3. n为奇数，n-1也是奇数，永远追不上。

总结

1. 链表中是否带环的判断，可以使用快慢指针法，形象的说法是龟兔赛跑法。
2. 快指针一次走2步，慢指针一次走1步，若带环，一定能够追上。快指针一次走3步，慢指针一次走1步，若带环，不一定能追上。

感谢大家的阅读！