二分法例题
- 第一题:搜索插入位置
- 解法一(左闭右闭)
- 解法二(左闭右开)
- 解法三(暴力求解)
- 第二题:在排序数组中查找元素的第一个和最后一个位置
- 解法一(左闭右闭)
- 第三题:x 的平方根
- 解法一(左闭右闭)
- 第四题:有效的完全平方数
- 解法一(左闭右闭)
- 解法三(暴力求解)
如果没看过我的上一篇建议可以看看上一篇的板子,下面几个题将会全部按板子展现哦!
戳这里直达—>二分法基础篇
第一题:搜索插入位置
这个题和二分法唯一的不同就是当它找不到对应的目标值时,不是" return -1 "了,而是需要返回的是它该插入位置的下标
题目直达链接
解法一(左闭右闭)
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left=0;
int right=nums.size()-1;//注意!!
int mid=0;
while(left<=right)//注意!!
{
mid=(right-left)/2+left;
//mid=((right-left)>>1)+left;这个更快,之间右移一位二进制相当于➗2
if(nums[mid]>target)
{
right=mid-1;
}
else if(nums[mid]<target)
{
left=mid+1;
}
else
return mid;
}
if(target>nums[mid])
//为了好理解套板子,这里只要简单的判断一下target在mid左边还是右边就可以了
return mid+1;
else
return mid;
}
解法二(左闭右开)
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left =0;
int right=nums.size();//注意!!
int mid=0;
while(left<right)//注意!!
{
// mid =(right-left)/2+left;
mid =((right-left)>>1)+left;
if(nums[mid]<target)
left=mid+1;
else if(nums[mid]>target)
right=mid;//注意!!
else
return mid;
}
if(nums[mid]<target)
return mid+1;
else
return mid;
}
};
空间复杂度是很优秀的

解法三(暴力求解)
由于本题的数组长度很短,所以使用暴力未尝不是一个好办法
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int i=0;
int num=nums.size();
if(nums[num-1]<target)
return num;
if(nums[0]>target)
return 0;
for(i=0;i<num;i++)
{
if(nums[i]>=target)
return i;
}
return 0;
}
};
事实证明确实很棒哈哈哈哈,因题而异,倒数后两个就是异
第二题:在排序数组中查找元素的第一个和最后一个位置
这个就
本题直达链接
解法一(左闭右闭)
这个题!我真的一下都不想多看了!!!感觉自己脑子好笨啊啊啊啊
浅浅的解释一下做题想法:很巧妙我只能说
这个题第一个解法
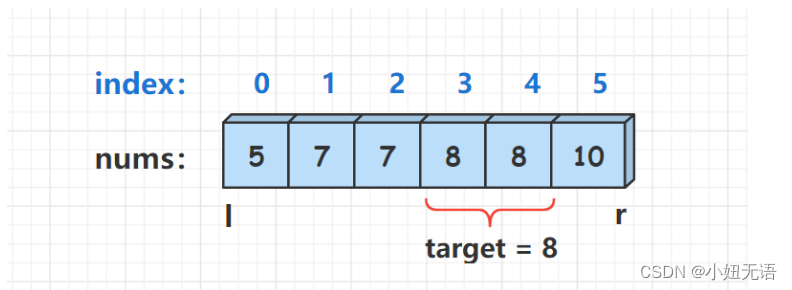
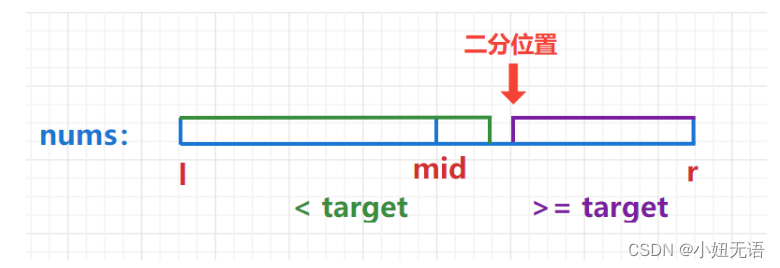
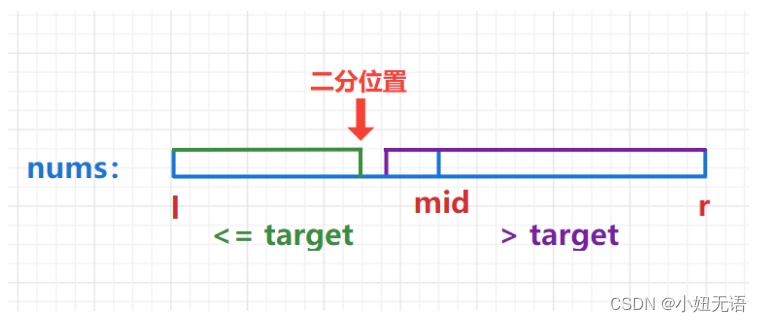
大家想想其实right其实就是相当于一个指针本来它是用来当作判定循环结束的条件,但是现在你想想如果right在 “ target == nums[mid] ”时,还让“ right=mid-1 ”,这时候如果左侧还有 “ target == nums[mid] ”, right继续左移,最后它就停在 “ target == nums[mid] ”元素的前一个,这就锁定了这个target的最前面(哎说不清了,如果还有伙计想不明白,私聊我,我亲自给观众老爷画图!)
sorry偷个图让大家看看
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int Getleft=rightGet(nums,target);
int Getright=leftGet(nums,target);
if(Getright-Getleft>=0)
return{Getleft,Getright};
else
return{-1,-1};
}
private:
int rightGet(vector<int>&nums,int target)
{
int left=0;
int right=nums.size()-1;//闭区间[left,right]
while(left<=right)
{
int mid=((right-left)>>1)+left;
if(nums[mid]<target)
left=mid+1;
else
right=mid-1;
}
return right+1;
}
int leftGet(vector<int>&nums,int target)
{
int left=0;
int right=nums.size()-1;//闭区间[left,right]
while(left<=right)
{
int mid=((right-left)>>1)+left;
if(nums[mid]<=target)
left=mid+1;
else
right=mid-1;
}
return left-1;
}
};
不怕大家笑话这个题我提交了14次,准确的是提交14次,改了n次,甚至因为这个题我还学了 “vector” (浅学),我发现这个是真的迷啊,是不是容器不能直接赋初值,必须要预分配(求教!)

剩下的几种做法的我后期补上,一定!
第三题:x 的平方根
可能大家第一次看见这个题会有点,为什么它可以用二分,问得好!
因为大家想想,“X"开平方一定 " <= X”,区间在 [0,X] ,这不就是二分了,有序数组,找目标值
题目直达链接
解法一(左闭右闭)
class Solution {
public:
int mySqrt(int x) {
int left=0;
int right=x;
long long mid=0;
while(left<=right)//只有在left>right时才会停止,这时x介于[right*right,left*left]之间,所以取整就取小喽,最后return right。
{
mid=((right-left)>>1)+left;
if(mid*mid>x)
right=mid-1;
else if(mid*mid<x)
left=mid+1;
else
return mid;
}
return right;
//有小伙伴可能卡这里了,想为啥return right
//咱一起设想一种情况当x=8,是mid是介于2与3之间,这时当mid=2时,mid*mid<x,left=2+1
//这时left=right,mid就自然等于right=3,但是此时mid*mid>8了,这时right进去进行减一,使得right=2
//其实大家想想,平方根无疑就两种情况一种就是可以直接开平方就return mid了,而另一种就是介于两个数之间,这时都需要进行上述的流程,一模一样的,所以现在只有right是满足条件的左区间,而left是右区间。
}
};
为啥这个题我只更了一个解法(第二种最近会更),暴力我觉得可能不太好题上说了 " 0 <= x <= 2^31 - 1 " ,看过我之前蓝桥杯的博客里面说过,2 ^31 - 1属于long long类型,这时间和空间可能浪费very much(上面可能有胡扯的成分在,所以我下个题写了暴力解法哈哈哈,两个题几乎一样)
第四题:有效的完全平方数
题目直达链接
这个题同上
解法一(左闭右闭)
class Solution {
public:
bool isPerfectSquare(int num) {
int left=0;
long long right=num;
long long mid=0;
while(left<=right)
{
mid=((right-left)>>1)+left;
if(mid*mid>num)
right=mid-1;
else if(mid*mid<num)
left=mid+1;
else
return true;//全是上个博客的板子
}
return false;
}
};
解法三(暴力求解)
class Solution {
public:
bool isPerfectSquare(int num) {
int ans=0;
for(int i=0;i<=num;i++){
if((long long)i*i<=num)
ans=i;
else
break;
}
if((long long)ans*ans==num)
return true;
else
return false;
}
};




![[附源码]计算机毕业设计springboot人事管理系统](https://img-blog.csdnimg.cn/20cef50c26be4e88b673a9b9602ac316.png)