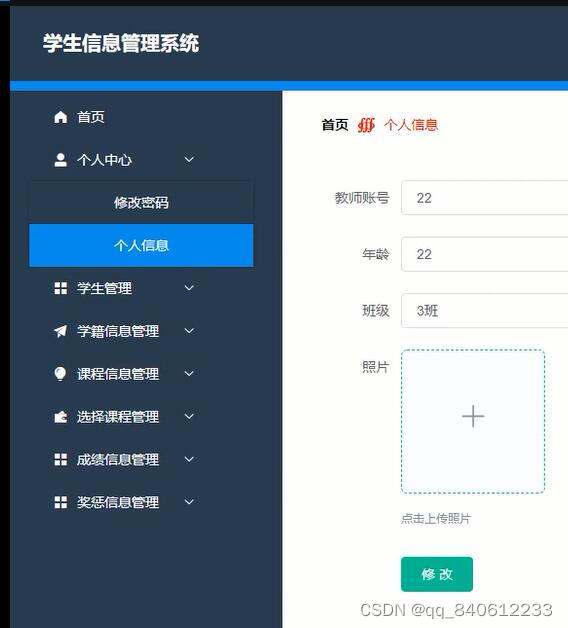
目录
- 知识框架
- No.0 引言
- No.1 数制与编码
- 一、进位计数制及其相互转换
- 二、BCD码
- 三、无符号的整数在计算机内部表示和运算
- 1、表示
- 2、加法、减法实现
- 四、带符号的整数在计算机内部表示和运算
- 1、表示
- 1.1、原码表示
- 1.2、原码形式实现加减法运算不行
- 1.3 补码表示
- 1.4 补码实现加法运算
- 1.5、补码实现减法运算
- 1.6、原码反码补码特性对比
- 1.7、移码表示
- 五、定点小数的表示和运算
- 5.1、原码中定点整数和定点小数
- 5.2、定点小数的反码补码表示
- 5.3、定点小数的加减运算
- No.2 奇偶校验码
- No.3 算术逻辑单元(ALU)
- 一、作用,大致原理
- 二、加法器的实现
- 1、一位全加器
- 2、串行加法器
- 3、并行加法器
知识框架
No.0 引言
探讨的两大主题:一步步递进
- 那么现在就需要探究 数据如何以2进制的形式在计算机中表示的呢??
- 那么还有就是计算机如何进行数据的算术和逻辑运算的??
No.1 数制与编码
一、进位计数制及其相互转换
我们平常使用的是10进制的数据,然而计算机能够识别的是2进制的01序列串。
主要是权重的不同。一方面符号表示权重,一方面符号的位置表示权重叫位权。比如975;
101001B、1652H、168D
- 其它进制数转换为十进制(不同的数码位在不同的位置有不一样的位权)
- 二进制<---->八进制、十六进制进行转换(三个二进制位进行组合、四个二进制位进行组合)
- 十进制转化为---->任意进制(整数和小数部分分别进行处理)。
- 真值和机器数;如果十进制数还带正负怎么办呢??如何在计算机中以2进制存储呢?
- 真值:符合人类习惯的数字
- 机器数:数字实际存到机器里的形式,正负号需要被“数字化”;0正1负。
二、BCD码
BCD码包括了三种即三种映射关系;那么引入BCD码是为了什么呢?
为什么说是二进制编码的十进制数?答:每四个比特的信息来对应上一个十进制位;
- 8421码:
- 余3码
- 2421码
三、无符号的整数在计算机内部表示和运算
无符号整数:即自然数=0+正整数:”0、1、2、3、4、、、、“
首先是没有符号,然后只是整数。
两个大问题:无符号整数,在计算机硬件中如何表示的呢?
:无符号整数,在计算机内部如何进行加法、减法运算怎么用硬件实现的呢?
1、表示
第一个大问题:无符号整数,在计算机硬件中如何表示的呢?
- 假设机器字长是8位的前提下;(当然现实是机器字长通常是64位or32位的)
- 也就是说机器字长是限制了每次多少位数字的运算’下面均以是8位的为举例子。
- ①:全部二进制位都是数值位,没有符号位,第i位的位权是2^i-1.
- ②:n bit无符号整数表示范围0~2^n-1,超出则溢出,意味着该计算机无法一次处理这么多
- ③:可以表示的最小的数全0,可以表示的最大的数全1.

2、加法、减法实现
第二个大问题:无符号整数,在计算机内部如何进行加法、减法运算怎么用硬件实现的呢?
- 计算机硬件如何做到无符号整数的加法呢?:从最低位开始,按位相加,并往更高位进位
- 在加法的时候也就是按照正常的二进制加法进行。而如果溢出的话也就会溢出截断了。

- 计算机硬件如何做到无符号整数的减法呢?:减法的话就不是平常那样了,要进行特殊处理
- ①”被减数” 不变 "减数”全部位按位取反、末位+1,减法变加法
- ②从最低位开始,按位相加,并往更高位进位(加法规则)
- ③最高位溢出丢弃,并不影响我们的结果。
- 那么为什么多此一举将减法变成加法呢???
- 因为:加法电路造价便宜,减法电路造价昂贵若可将减法转变为加法,所以将减法操作变成等价的加法操作,可以更省钱
- 那么为什么可以这样取反+1等就可以变化等价呢?这里是数论的知识了。

四、带符号的整数在计算机内部表示和运算
带符号整数:即整数:”-4、-3、-2、-1、0、1、2、3、4、、、、“
首先是有符号,然后只是整数。
两个大问题:带符号整数,在计算机硬件中如何表示的呢?
:带符号整数,在计算机内部如何进行加法、减法运算怎么用硬件实现的呢?
后面有个总结就是所有的带符号整数的运算都要先将原码转化为补码然后再进行运算。
1、表示
第一个大问题:带符号整数,在计算机硬件中如何表示的呢?
- 为什么带符号整数的表示有原码、反码、补码这些东西呢?
- 是因为在计算机内部我们表示一个带符号的数值的时候,同一个含义用不同的编码方式表示
- 当然不同的编码表示有各自的优点和缺点;
1.1、原码表示
首先带符号整数表示中现以 原码为例子:
- 假设机器字长是8位的前提下;(当然现实是机器字长通常是64位or32位的)
- 所以由于硬件的限制,那么带符号的整数表示的它的比特位位数是有上限的;
- 也就是说机器字长是限制了每次多少位数字的运算’下面均以是8位的为举例子。
- ①符号位“0/1”对应“正/负”,剩余的数值位表示真值的绝对值
- ②若机器字长n+1位,带符号整数的原码表示范围: 一(2^n-1) ≤x ≤ 2^n-1
- ③真值0有两种形式:+0和-0 ,[+0]:=0,0000000;[-0]原 =1, 0000000

1.2、原码形式实现加减法运算不行
基于原码表示的有符号整数,如何实现加减法呢?
- 如果我们按照无符号的整数进行 从最低位开始往上加,按位相加(❌)。
- 但是我们在无符号的整数表示的时候最高位是表示的数值信息,但在这里是符号的信息。所以不行。
- 原码的缺点:符号位不能参与运算,需要设计复杂的硬件电路才能处理,费钱!贵!(也可以但是贵)
- 所以 科学家发明了这样的方法:用补码表示真值–符号位可以参与运算。(所以参与运算前都要转化为补码)
- 即我们在用原码进行实现加减法的时候不方便,所以要将原码的表示形式转化为等价的补码表示即可。

1.3 补码表示
如何进行补码的表示呢在计算机的硬件之中??
其实是 从原码转化过来的:原码–>反码–>补码
不管是原码、反码、补码、这三个的最高位都反映了符号位(0正1负),
所以可能转化为10000000吗这个形式?是的,当一个有符号数在二进制下的表示的最高位为1时,表示该数是一个负数。在进行原码转补码的时候,如果刚好进位到最高位,将会得到补码的最高位为1,即10000000。这个补码所代表的负数通常是最小的负数,也就是-128。因此,当进行原码转化为补码的时候,可能转换得到10000000这个形式。
只不过是补码的符号位可以参与运算。?

如何快速的将 原码和补码进行相互转换呢?两种方式:
第一种计算机中形式:那么计算机中硬件中是如何实现补码到原码的转换的呢?
计算机中是这样实现的:从补码出发,符号位不变,然后数值位取反,最后+1
第二种手动形式:如下图:

1.4 补码实现加法运算
- 从最低位开始,按位相加,(符号位参与运算),并且往最高位进位。
- 最后我们只保留更低的八位bit,最前边的一位给它丢弃。
- 最终得到的结果也是补码的形式,而想要知道数值为多少就需要将这个结果补码转化为原码。

1.5、补码实现减法运算
- 因为加法电路造价便宜,减法电路造价昂贵。若可将减法转变为加法,省钱!
- 那么怎么转呢?
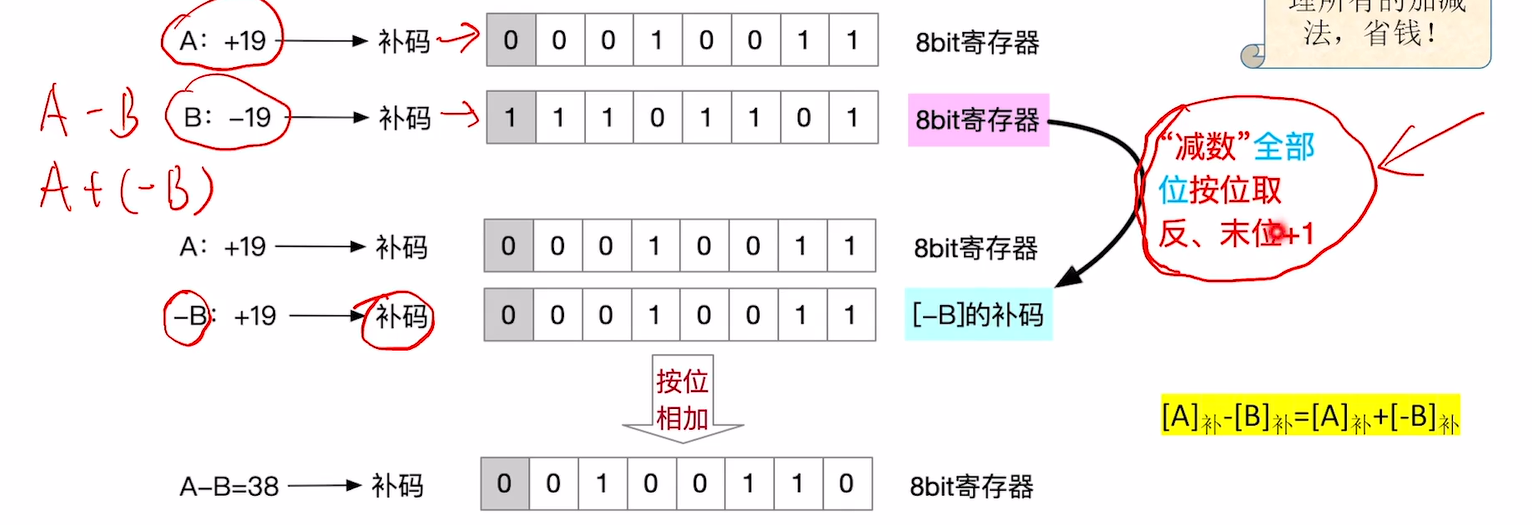
- 即因为A-B=A+(-B); 然后将这些原码转化为补码然后进行加法运算,然后再将最终的补码结果转化为原码结果。
- 由于计算机在一开始就把所有的原码转化为补码了;
- 即“被减数(补码形式)”不变,【“减数(补码形式)”全部位按位取反、末位+1】变为[-B]补,减法变加法
- (补码形式)从最低位开始,按位相加,并往更高位进位。得到最终结果补码形式。
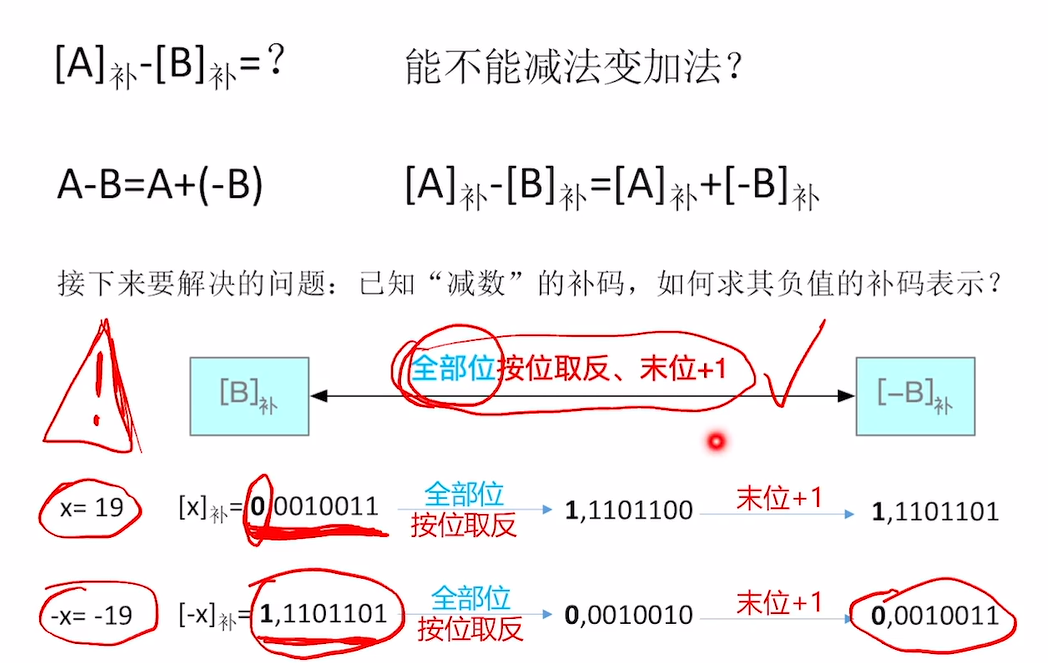
一个具体的带符号数的减法例子:
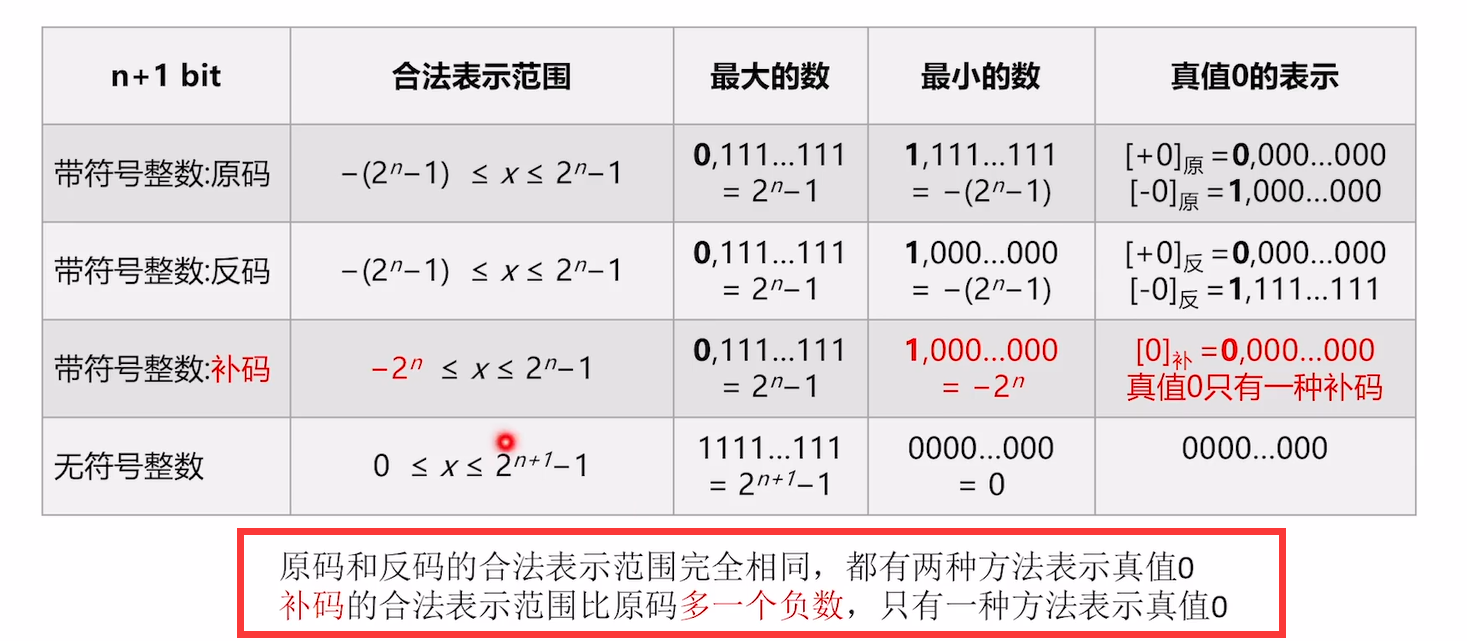
1.6、原码反码补码特性对比
下面的东西都是在 n+1 位bit的合法表示范围。
各种特性总结如下:
因为补码的那个最小负数转化为位数相同的原码是不可能的。因为范围限制。
溢出问题:关于两个数A和B进行某种运算后,是否发生溢出?―-手算做题可以带入十进制验证,是否超出合法范围
A=-64,B=-64;如果题目是 用 原码进行 讲述 的,那么最后结果保存用原码的话就会溢出;原码范围是-127~127;
而如果A和B都是补码的形式的话,那么最后结果保存是不会溢出的,因为补码范围是-128~127;
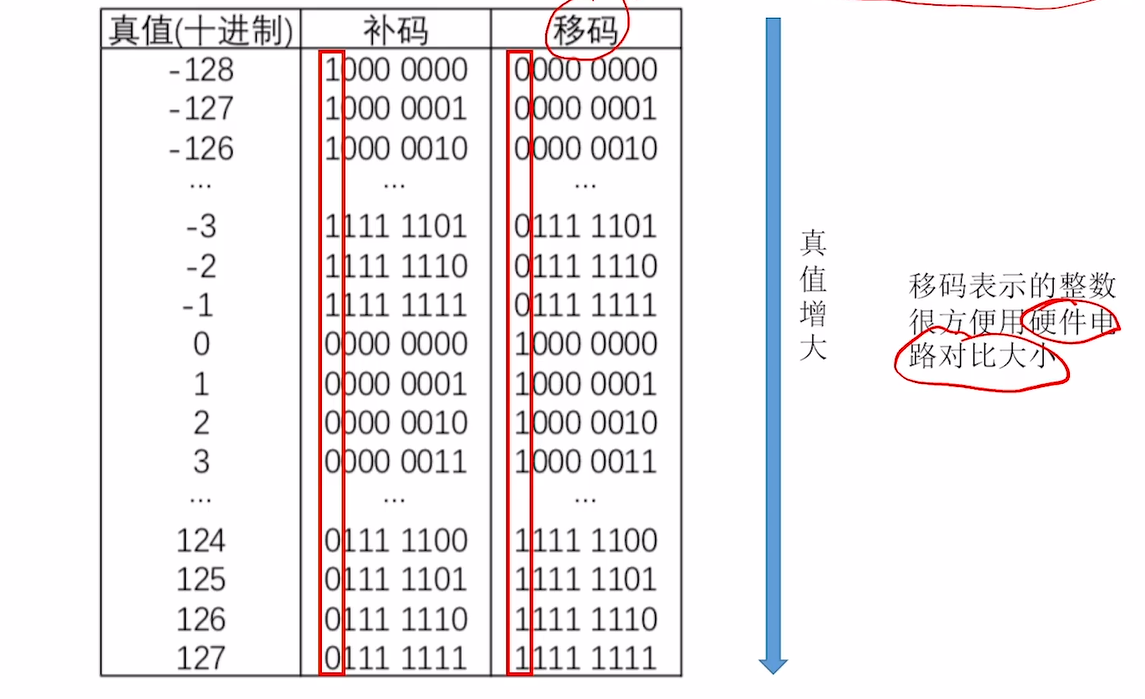
1.7、移码表示
那么怎么得到移码呢?
从补码得到:补码的符号位取反即可。
注意:移码只能用于表示整数(且是带符号的整数)
- 因为移码是从补码进行转化的,所以一些补码的特性就可以按照着来;
- 补码0的形式只有一种即0,00000000则[0]的移码就有一种:1,00000000
- 那么补码的 数据范围也是 -128~127(前提是n+1位的bit);

五、定点小数的表示和运算
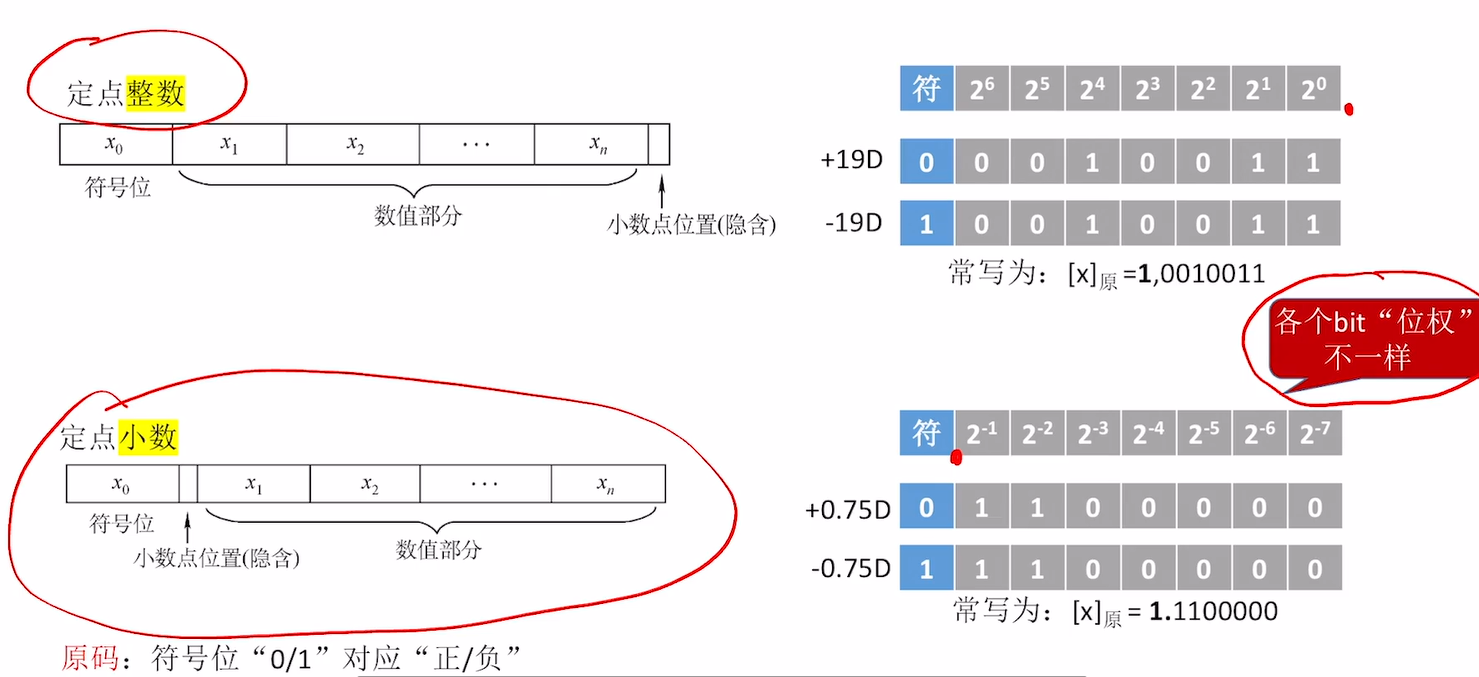
定点的意思是什么呢?定点的意思是小数点的位置固定。
定点数:定点整数即带符号整数(也就是小数点的位置固定在了最后一位的右下角
:定点小数(也就是小数点的位置固定在了 符号位的右下角。
- 对于第一个大问题表示中,其实也只是臆想,不是一个bit位来存储的。简称规定。
- 定点整数的编码表示:原码、反码、补码、移码
- 定点小数的编码表示:原码、反码、补码
5.1、原码中定点整数和定点小数
下面的都是以8bit位来进行说明的。
小数点的位置不一样,导致的 各个bit“位权”不一样。
5.2、定点小数的反码补码表示
与带符号整数的 原码–》反码、补码的转化形式一模一样,
5.3、定点小数的加减运算
对两个定点小数A、B进行加法/减法时,需要先转换为补码。
计算机硬件如何做定点小数补码的加法:
①从最低位开始,按位相加(符号位参与运算),并往更高位进位,
②然后再转
计算机硬件如何做定点小数补码的减法:
①“被减数”不变,“减数”全部位按位取反、末位+1,减法变加法;
②从最低位开始,按位相加,并往更高位进位
下面是定点整数和定点小数的比较:如下图:
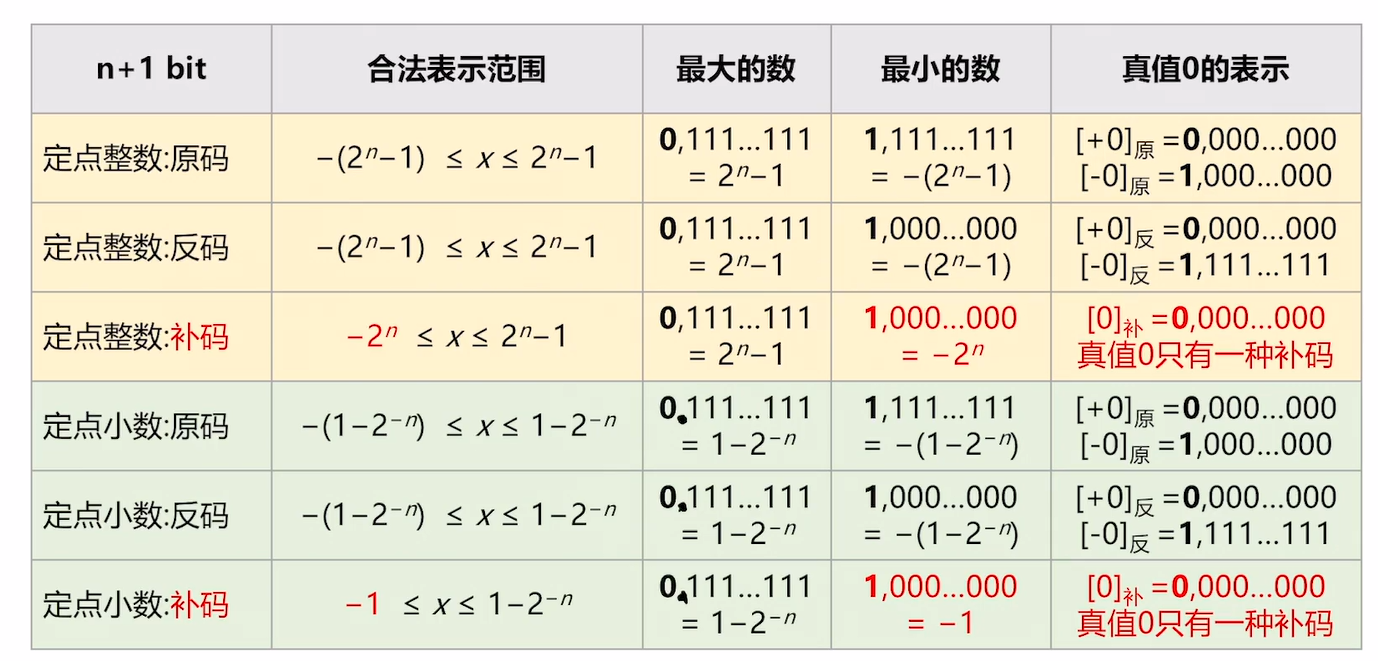
小数补码的加法运算:也是先将各个转化为补码再看
反正无论是整数还是小数在进行加法运算的时候,都是要按照那个方法进行
因为计算机为了便宜,计算电路都是一样的,
No.2 奇偶校验码
因为在传输的过程中会出现 错误之类的,所以我们必须考虑到数据的校验。
可能计算机元器件发生故障什么之类的,可能由于环境的因素噪音的干扰,可能会发生了位错误;01–00
那么我们该怎么才能发现错误呢?
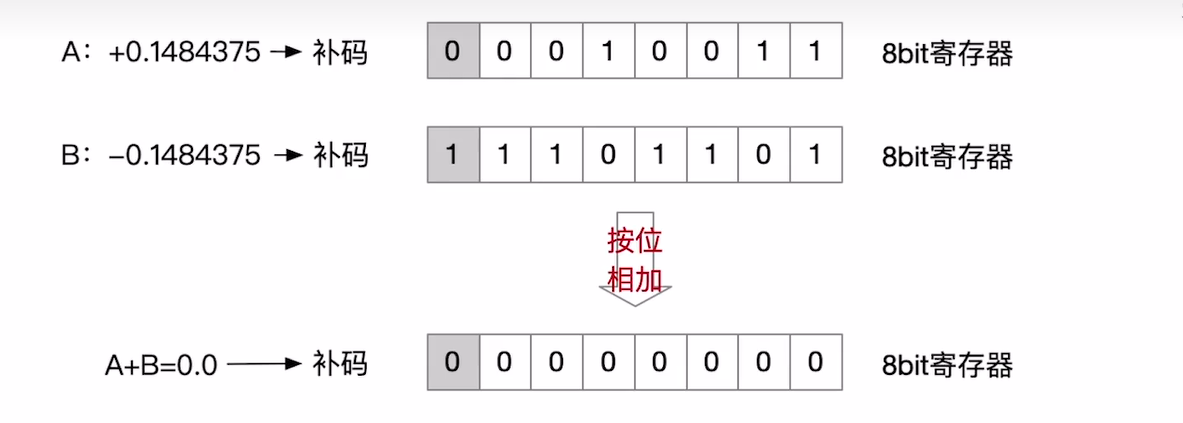
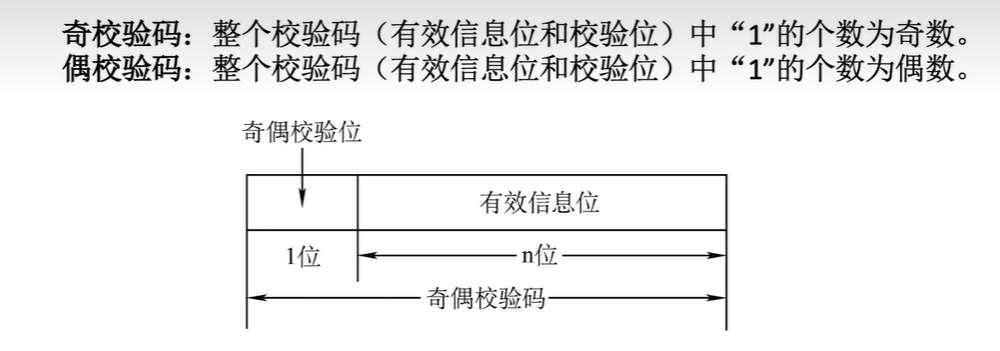
下面是一种可以发现错误的编码机制:奇偶校验
- 校验原理:增加一个冗余的校验位bit。
- 那么怎么检测出错误呢?
- 假设我们采用偶校验策略:一个bit发生跳变直接断定发生错误了,那么发生两个bit发生跳变呢?(检测不出来局限性)
No.3 算术逻辑单元(ALU)
一、作用,大致原理
下面是介绍的ALU的一些基本作用:
- 算术运算:加、减、乘、除等
- 逻辑运算:与、或、非、异或等
- 辅助功能:移位、求补等
二、加法器的实现
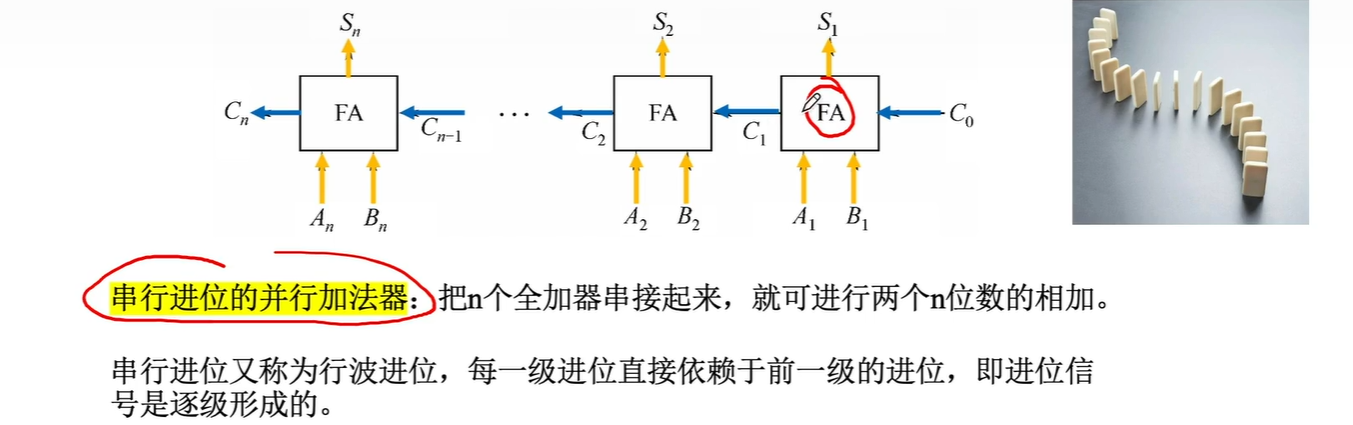
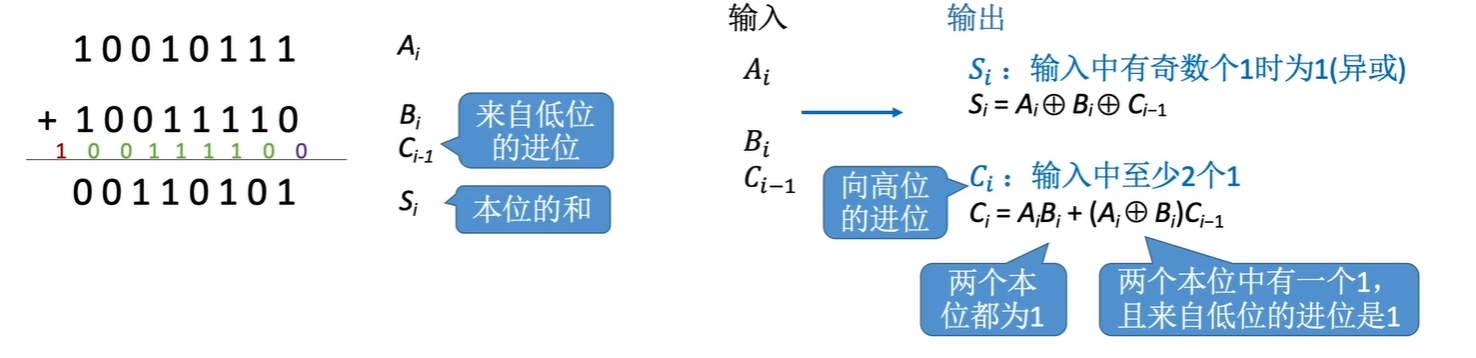
1、一位全加器
是有一个进位的计数的。
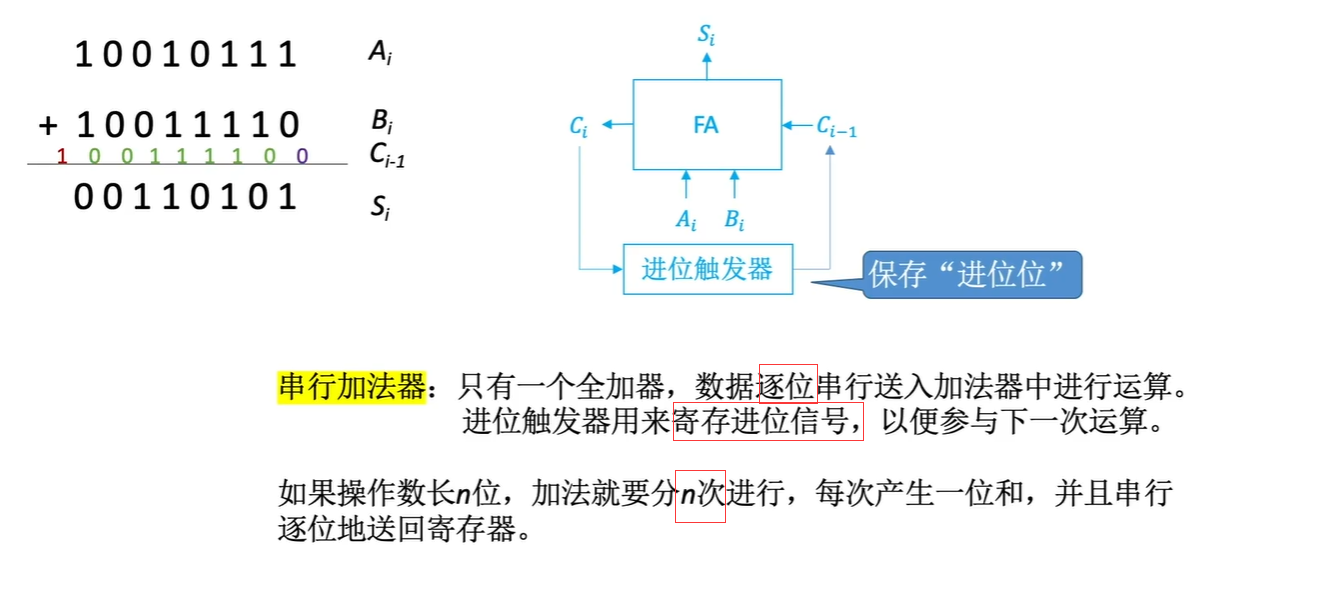
2、串行加法器
如何使用上面的一位全加器 如何实现 多位的加法。循环使用。像那个RNN样的图差不多。
3、并行加法器