蚁群算法ACS处理旅行商问题TSP【Java实现】

news2025/1/24 1:27:16

1. 介绍

蚁群算法是一种群体智能算法，模拟了蚂蚁寻找食物时的行为，通过蚂蚁之间的信息交流和合作，最终实现全局最优解的寻找【是否找得到和迭代次数有关】。

蚁群算法的基本思想是将搜索空间看作一个由节点组成的图，每个节点代表一种可能的解决方案，而边则代表两个节点之间的关联关系。在这个图中，一只蚂蚁在搜索过程中会沿着路径移动，每经过一个节点，它会留下信息素，这些信息素会吸引其他蚂蚁跟随它的路径。同时，蚂蚁在移动的过程中也会依据信息素的浓度，更有可能选择路径上信息素浓度较高的节点。

蚂蚁群算法的核心是信息素的更新和挥发。信息素的更新是指当一只蚂蚁找到一个更优的解决方案时，它会在路径上留下更多的信息素，这样其他蚂蚁就更有可能跟随这个路径，从而加速搜索过程。信息素的挥发则是指在一定的时间间隔内，信息素会自然挥发，这样可以避免信息素积累过多导致搜索过早收敛。

蚂蚁群算法是一种高效的全局优化算法，广泛应用于组合优化、信号处理、机器学习、图形图像处理等领域。

2. 主体公式

蚁群算法中，蚂蚁到达每个点的概率是根据该点的信息素浓度和距离来计算的。具体地说，设当前蚂蚁所在的城市为 i i i ，已经访问过的城市集合为 J J J ，未访问过的城市集合为 K K K ，则蚂蚁由 i i i 到达城市 j j j 的概率可以用如下公式计算：
p i , j = [ τ i , j ] α [ η i , j ] β ∑ k ∈ K [ τ i , k ] α [ η i , k ] β p_{i,j}=\frac{[\tau_{i,j}]^{\alpha}[\eta_{i,j}]^{\beta}}{\sum\limits_{k\in K} [\tau_{i,k}]^{\alpha}[\eta_{i,k}]^{\beta}} pi,j​=k∈K∑​[τi,k​]α[ηi,k​]β[τi,j​]α[ηi,j​]β​

其中， τ i , j \tau_{i,j} τi,j​ 表示从城市 i i i 到城市 j j j 的信息素浓度， η i , j \eta_{i,j} ηi,j​ 表示从城市 i i i 到城市 j j j 的距离的倒数， α \alpha α 和 β \beta β 分别表示信息素重要程度因子和距离重要程度因子，通常 α \alpha α 和 β \beta β 的值都为正数。在选择下一个要访问的城市时，蚂蚁会根据这个概率进行随机选择，不难发现，信息素浓度越大，城市间的距离越短，对应的概率就会越大。

对于一只蚂蚁走过的路径上的每条边 $ (i,j)$ ，它在该边上留下的信息素增量为：
Δ τ i j = q L k \Delta \tau_{ij} = \dfrac{q}{L_k} Δτij​=Lk​q​
其中， q q q 是信息素增加强度系数， L k L_k Lk​ 表示第 k k k 只蚂蚁完成路径的长度。

参数代码形式如下👇：

	// 距离矩阵
	private double[][] distance;
	// 信息素矩阵
	private double[][] pheromone; 
	// 城市数量
	private int cityNum; 
	// 蚂蚁数量
	private int antNum; 
	// 最大迭代次数
	private int maxGen; 
	// 信息素因子
	private double alpha; 
	// 距离重要程度因子
	private double beta; 
	// 信息素挥发因子
	private double rho; 
	// 信息素增加强度系数
	private double q; 
	// 最优路径
	private int[] bestTour; 
	// 最优路径长度
	private double bestLength;

3. 算法实现步骤

  1. 初始化信息素矩阵，初始时各路径上信息素浓度相同

    	// 初始化信息素矩阵
	private void initPheromone() {
		// 信息素初始值
		double initPheromone = 1.0 / (cityNum * distance[0][1]);
		for (int i = 0; i < cityNum; i++) {
			for (int j = 0; j < cityNum; j++) {
				// 各条路径的信息素浓度
				pheromone[i][j] = initPheromone;
			}
		}
	}

  2. 第一只蚂蚁从随机一个城市出发，综合信息素浓度以及到达各城市的距离，计算得到公式 p i j p_{ij} pij​ 的分子，存储在数组 p p p 中，同时将分母用累加和 s u m sum sum 存储

    一个圆形转盘区域标记为 [ 0 , 1 ) [0,1) [0,1) ， ∑ p i j = 1 \sum p_{ij} = 1 ∑pij​=1

  3. 选择下一个城市采用轮盘赌的方式，即产生一个在 [ 0 , 1 ) [0,1) [0,1) 随机数 r a n d rand rand 作为圆形转盘的指针指向的位置，利用 t m p tmp tmp 【 p i j p_{ij} pij​ 累加和】锁定轮盘上的各个区域，一旦 t m p ≥ r a n d tmp \ge rand tmp≥rand ，说明当前城市就是下一个目的地，将此城市在 v i s i t e d visited visited 中标记，同时将其加入访问顺序 t o u r tour tour 中。

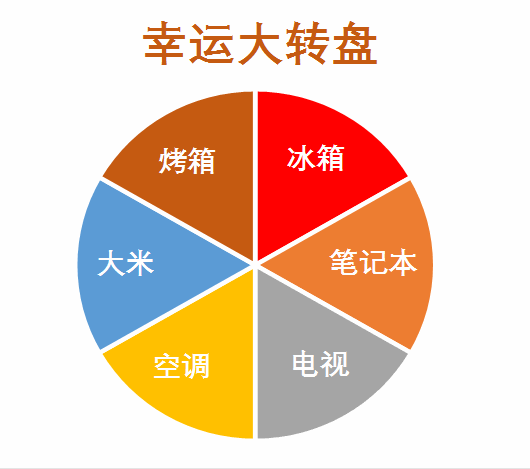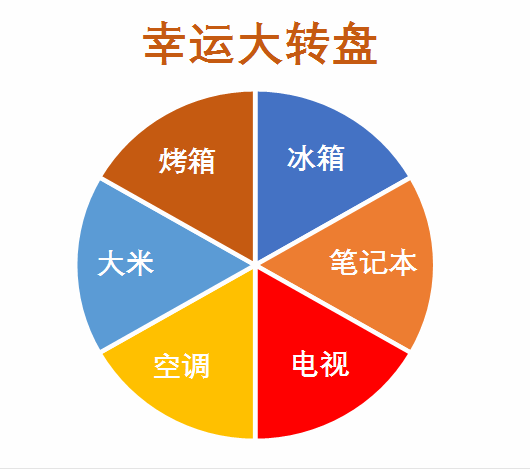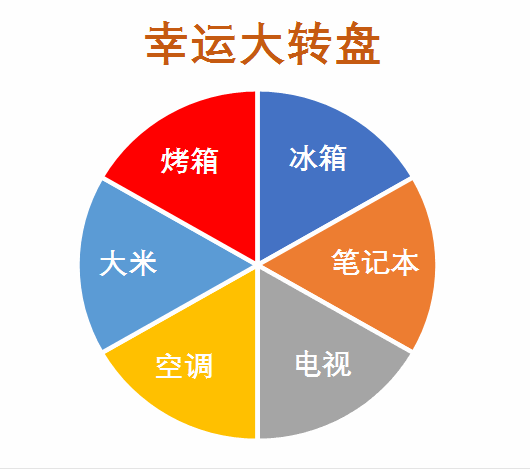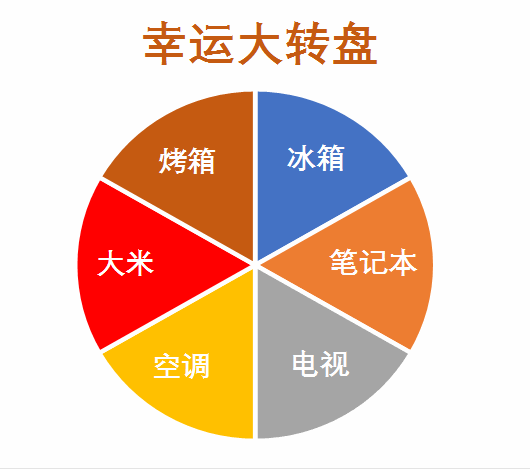
    4e1eb5ff3c9d479796116fc341ac826e

    用此方法访问所有节点后，返回范围顺序 t o u r tour tour

    	// 蚂蚁移动
	// pheromone : 信息素矩阵
	private int[] antMove(double[][] pheromone) {
		// 存储依次到达的城市序号
		int[] tour = new int[cityNum];
		boolean[] visited = new boolean[cityNum];
		Random random = new Random();
		// 生成一个不大于 cityNum 的伪随机整数
		int start = random.nextInt(cityNum);
		// 从 start 城市出发，此城市标记为已访问
		visited[start] = true;
		// 第一个访问 start 城市
		tour[0] = start;
		for (int i = 1; i < cityNum; i++) {
			// 当前蚂蚁所在的城市
			int curCity = tour[i - 1];
			// p 存放概率公式的分子部分
			double[] p = new double[cityNum];
			// sum 存放概率公式的分母部分
			double sum = 0.0;
			for (int j = 0; j < cityNum; j++) {
				// 城市 j 没有被访问过
				if (!visited[j]) {
					p[j] = Math.pow(pheromone[curCity][j], alpha) * Math.pow(1.0 / distance[curCity][j], beta);
					sum += p[j];
				}
			}
			// 用 [0,1] 范围的伪随机数代替轮盘针转到的位置
			double rand = random.nextDouble()  ;
			double tmp = 0.0;
			int nextCity = 0;
			for (int j = 0; j < cityNum; j++) {
				if (!visited[j]) {
					// 每个概率 p[j]/sum 代表轮盘上的一块区域
					// tmp 累积值代表指针到的位置
					tmp += p[j]/sum;
					// 超过 rand ，说明来到了这个区间，即当前城市就是目标城市
					if (tmp >= rand) {
						nextCity = j;
						break;
					}
				}
			}
			// 标记城市为已访问
			visited[nextCity] = true;
			// 记录蚂蚁的下个城市目的地
			tour[i] = nextCity;
		}
		return tour;
	}

  4. 由于知道城市访问顺序 t o u r tour tour ，因此不难得到访问总距离 t o u r L e n g t h tourLength tourLength ，如果这个总距离小于 b e s t T o u r bestTour bestTour ，说明这是更优的解法，因此更新 b e s t T o u r bestTour bestTour 和 b e s t L e n g t h bestLength bestLength

  5. 蚂蚁访问完各个城市后开始更新各路径上的信息素增量 Δ τ \Delta\tau Δτ ， Δ τ \Delta\tau Δτ 由是信息素增加强度系数 Q Q Q，和 L L L 蚂蚁完成路径的长度决定

  6. 当所有蚂蚁都将城市访问完毕后，将信息素增量 Δ τ \Delta\tau Δτ 更新至原路径上的信息素中，同时还需要考虑信息素的挥发，最终得到第一次迭代后的信息素矩阵情况

    	// 更新信息素矩阵
	private void updatePheromone() {
		// 蚂蚁在经过路径上留下的信息增量
		double[][] deltaPheromone = new double[cityNum][cityNum];
		for (int i = 0; i < antNum; i++) {
			// 单只蚂蚁根据当前信息素矩阵而得到的访问顺序
			int[] tour = antMove(pheromone);
			// 当前蚂蚁访问的长度
			double tourLength = getTourLength(tour);
			// 说明可以优化
			if (tourLength < bestLength) {
				// 更新最短路径
				bestLength = tourLength;
				// 由于有了最短路径，因此存储的访问路径也需要更新
				System.arraycopy(tour, 0, bestTour, 0, cityNum);
			}
			for (int j = 0; j < cityNum - 1; j++) {
				int city1 = tour[j];
				int city2 = tour[j + 1];
				// 信息素增量Δτ，只要有蚂蚁经过就会变多
				deltaPheromone[city1][city2] += q / tourLength;
				deltaPheromone[city2][city1] = deltaPheromone[city1][city2];
			}
			deltaPheromone[tour[cityNum - 1]][tour[0]] += q / tourLength;
			deltaPheromone[tour[0]][tour[cityNum - 1]] = deltaPheromone[tour[cityNum - 1]][tour[0]];
		}
		for (int i = 0; i < cityNum; i++) {
			for (int j = 0; j < cityNum; j++) {
				// 原来的信息素挥发了部分，同时新的信息素又增加了一些
				pheromone[i][j] = pheromone[i][j] * (1.0 - rho) + deltaPheromone[i][j];
			}
		}
	}

  7. 多次迭代后可以得到最优路径，存放在 b e s t T o u r bestTour bestTour 中，最短路径长度存放于 b e s t L e n g t h bestLength bestLength

    	// 运行蚁群算法
	public void run() {
		initPheromone();
		// 迭代次数
		for (int i = 0; i < maxGen; i++) {
			updatePheromone();
		}
		System.out.println("迭代"+maxGen+"次后，最优的路径长度：" + bestLength);
		System.out.println("最优路径为：");
		for (int i = 0; i < cityNum; i++) {
			System.out.print(bestTour[i] + " ");
		}
	}

  8. 样例测试

    public class AntColonyOptimizationTest {
    public static void main(String[] args) {
        // 城市数目
        int cityNum = 4;
        // 蚂蚁数目
        int antNum = 20;
        // 迭代次数
        int maxGen = 100;
        // 信息素重要程度因子
        double alpha = 1.0;
        // 距离的重要程度因子
        double beta = 5.0;
        // 信息素挥发因子
        double rho = 0.5;
        // 信息素增加强度系数
        double q = 1;

        // 初始化距离矩阵【无向图】
        double[][] distance= {{0,58,87,64},{58,0,53,49},{87,53,0,88},{64,49,88,0}};
        System.out.println("距离矩阵distance为：");
        for (double[] ds : distance) {
			System.out.println(Arrays.toString(ds));
		}
        AntColonyOptimization aco=new AntColonyOptimization(distance, antNum, maxGen, alpha, beta, rho, q);
        aco.run();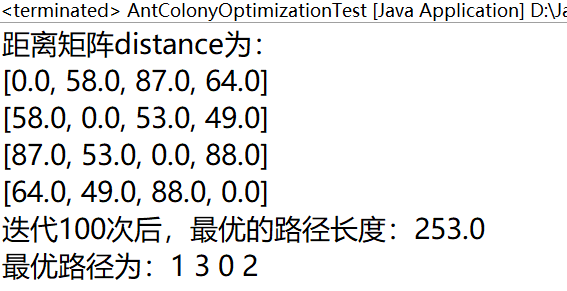
    }
}
    image-20230513181850250

4. 完整代码

4.1 AntColonyOptimization类

package aca;

import java.util.Random;
public class AntColonyOptimization {
	 // 距离矩阵
	private double[][] distance;
	// 信息素矩阵
	private double[][] pheromone; 
	// 城市数量
	private int cityNum; 
	// 蚂蚁数量
	private int antNum; 
	// 最大迭代次数
	private int maxGen; 
	// 信息素因子
	private double alpha; 
	// 距离重要程度因子
	private double beta; 
	// 信息素挥发因子
	private double rho; 
	// 信息素增加强度系数
	private double q; 
	// 最优路径
	private int[] bestTour; 
	// 最优路径长度
	private double bestLength; 

	public AntColonyOptimization(double[][] distance, int antNum, int maxGen, double alpha, double beta, double rho,
			double q) {
		this.distance = distance;
		this.cityNum = distance.length;
		this.antNum = antNum;
		this.maxGen = maxGen;
		this.alpha = alpha;
		this.beta = beta;
		this.rho = rho;
		this.q = q;
		this.pheromone = new double[cityNum][cityNum];
		this.bestTour = new int[cityNum];
		this.bestLength = Double.MAX_VALUE;
	}

	// 初始化信息素矩阵
	private void initPheromone() {
		// 信息素初始值
		double initPheromone = 1.0 / (cityNum * distance[0][1]);
		for (int i = 0; i < cityNum; i++) {
			for (int j = 0; j < cityNum; j++) {
				// 各条路径的信息素浓度
				pheromone[i][j] = initPheromone;
			}
		}
	}

	/**
	 * 
	 * @param pheromone 信息素矩阵
	 * @return 蚂蚁依次访问城市的顺序
	 */
	// 蚂蚁移动
	private int[] antMove(double[][] pheromone) {
		// 存储依次到达的城市序号
		int[] tour = new int[cityNum];
		boolean[] visited = new boolean[cityNum];
		Random random = new Random();
		// 生成一个不大于 cityNum 的伪随机整数
		int start = random.nextInt(cityNum);
		// 从 start 城市出发，此城市标记为已访问
		visited[start] = true;
		// 第一个访问 start 城市
		tour[0] = start;
		for (int i = 1; i < cityNum; i++) {
			// 当前蚂蚁所在的城市
			int curCity = tour[i - 1];
			// p 存放概率公式的分子部分
			double[] p = new double[cityNum];
			// sum 存放概率公式的分母部分
			double sum = 0.0;
			for (int j = 0; j < cityNum; j++) {
				// 城市 j 没有被访问过
				if (!visited[j]) {
					p[j] = Math.pow(pheromone[curCity][j], alpha) * Math.pow(1.0 / distance[curCity][j], beta);
					sum += p[j];
				}
			}
			// 用 [0,1] 范围的伪随机数代替轮盘针转到的位置
			double rand = random.nextDouble()  ;
			double tmp = 0.0;
			int nextCity = 0;
			for (int j = 0; j < cityNum; j++) {
				if (!visited[j]) {
					// 每个概率 p[j]/sum 代表轮盘上的一块区域
					// tmp 累积值代表指针到的位置
					tmp += p[j]/sum;
					// 超过 rand ，说明来到了这个区间，即当前城市就是目标城市
					if (tmp >= rand) {
						nextCity = j;
						break;
					}
				}
			}
			// 标记城市为已访问
			visited[nextCity] = true;
			// 记录蚂蚁的下个城市目的地
			tour[i] = nextCity;
		}
		return tour;
	}

	// 更新信息素矩阵
	private void updatePheromone() {
		// 蚂蚁在经过路径上留下的信息增量
		double[][] deltaPheromone = new double[cityNum][cityNum];
		for (int i = 0; i < antNum; i++) {
			// 单只蚂蚁根据当前信息素矩阵而得到的访问顺序
			int[] tour = antMove(pheromone);
			// 当前蚂蚁访问的长度
			double tourLength = getTourLength(tour);
			// 说明可以优化
			if (tourLength < bestLength) {
				// 更新最短路径
				bestLength = tourLength;
				// 由于有了最短路径，因此存储的访问路径也需要更新
				System.arraycopy(tour, 0, bestTour, 0, cityNum);
			}
			for (int j = 0; j < cityNum - 1; j++) {
				int city1 = tour[j];
				int city2 = tour[j + 1];
				// 信息素增量Δτ，只要有蚂蚁经过就会变多
				deltaPheromone[city1][city2] += q / tourLength;
				deltaPheromone[city2][city1] = deltaPheromone[city1][city2];
			}
			deltaPheromone[tour[cityNum - 1]][tour[0]] += q / tourLength;
			deltaPheromone[tour[0]][tour[cityNum - 1]] = deltaPheromone[tour[cityNum - 1]][tour[0]];
		}
		for (int i = 0; i < cityNum; i++) {
			for (int j = 0; j < cityNum; j++) {
				// 原来的信息素挥发了部分，同时新的信息素又增加了一些
				pheromone[i][j] = pheromone[i][j] * (1.0 - rho) + deltaPheromone[i][j];
			}
		}
	}

	/**
	 * 
	 * @param tour 蚂蚁访问顺序
	 * @return 当前访问顺序对应的路径长度
	 */
	// 获取路径长度
	private double getTourLength(int[] tour) {
		double tourLength = 0.0;
		for (int i = 0; i < cityNum - 1; i++) {
			// 将路径中城市间的距离相加
			tourLength += distance[tour[i]][tour[i + 1]];
		}
		// 最后还要返回起点
		tourLength += distance[tour[cityNum - 1]][tour[0]];
		return tourLength;
	}

	// 运行蚁群算法
	public void run() {
		initPheromone();
		// 迭代次数
		for (int i = 0; i < maxGen; i++) {
			updatePheromone();
		}
		System.out.println("迭代"+maxGen+"次后，最优的路径长度：" + bestLength);
		System.out.print("最优路径为：");
		for (int i = 0; i < cityNum; i++) {
			System.out.print(bestTour[i] + " ");
		}
	}
}

4.2 AntColonyOptimizationTest类

package aca;
import java.util.Arrays;

import aca.AntColonyOptimization;
public class AntColonyOptimizationTest {
    public static void main(String[] args) {
        // 城市数目
        int cityNum = 4;
        // 蚂蚁数目
        int antNum = 20;
        // 迭代次数
        int maxGen = 100;
        // 信息素重要程度因子
        double alpha = 1.0;
        // 距离的重要程度因子
        double beta = 5.0;
        // 信息素挥发因子
        double rho = 0.5;
        // 信息素增加强度系数
        double q = 1;

        // 初始化距离矩阵【无向图】
        double[][] distance= {{0,58,87,64},{58,0,53,49},{87,53,0,88},{64,49,88,0}};
//        double[][] distance = new double[cityNum][cityNum];
//        for (int i = 0; i < cityNum; i++) {
//            for (int j = i; j < cityNum; j++) {
//                if (i == j) {
//                    distance[i][j] = 0.0;
//                } else {
//                    double d = Math.random() * 100;
//                    // 城市 i 到城市 j 的距离
//                    distance[i][j] = d;
//                    distance[j][i] = d;
//                }
//            }
//        }
        System.out.println("距离矩阵distance为：");
        for (double[] ds : distance) {
			System.out.println(Arrays.toString(ds));
		}
        AntColonyOptimization aco=new AntColonyOptimization(distance, antNum, maxGen, alpha, beta, rho, q);
        aco.run();
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/521743.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux awk [-v] {print} 命令

Linux awk [-v] {print} 命令

AWK 是一种处理文本文件的语言&#xff0c;是一个强大的文本分析工具。 语法&#xff1a;语法&#xff1a;awk 条件1 {动作 1} 条件 2 {动作 2} … 文件名 awk是处理文本文件的语言&#xff0c;所以要传入文本数据供其处理&#xff08;文件逐行读入&#xff09;&#xff0c;…
阅读更多...
合宙Air780e C-SDK开发

合宙Air780e C-SDK开发

Air78e简介 AirXXXE系列模组&#xff0c;是合宙通信基于移芯EC618平台设计研发的新款4G Cat.1模组。 Air780e的资料点击这里打开。 Air78e开发板简介 一代 IPEX 天线连接器&#xff08;选配&#xff09;4G 弹簧天线一个下载/调试串口&#xff0c;两个通用串口IO 口默认电平…
阅读更多...
电子电气架构——车辆电子电气架构的网络安全汇总

电子电气架构——车辆电子电气架构的网络安全汇总

我是穿拖鞋的汉子，魔都中坚持长期主义的工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 本文主要分享关于车辆电子电气架构的网络安全常见隐患和对应现阶段解决办法。 背景信息 不知道是否还记得《速度与激情8》中黑客Cipher通过网络侵入车辆，…
阅读更多...
PyTorch2.0向后兼容性和加速效果浅探

PyTorch2.0向后兼容性和加速效果浅探

前言 在PyTorch2022开发者大会上&#xff0c;PyTorch团队发布了一个新特性——torch.compile&#xff0c;将PyTorch的性能推向了新的高度&#xff0c;称这个新版本为PyTorch2.0。torch.compile的引入不影响之前的功能&#xff0c;其是一个完全附加和可选的功能&#xff0c;因此…
阅读更多...
Linux系统调用函数（300多个）

Linux系统调用函数（300多个）

前言&#xff1a;这里只是给出中文描述&#xff0c;方便浏览熟悉&#xff0c;具体情况建议去具体环境&#xff08;Linux系统&#xff09;下执行 1&#xff09;man 2 systemcalls &#xff08;查看所有系统调用函数&#xff09;&#xff1b;2&#xff09;man 2 open &#xff08…
阅读更多...
Codeforces Round 872 (Div. 2)

Codeforces Round 872 (Div. 2)

Problem - D2 - Codeforces 思路&#xff1a; 我们设good点到所有k点的距离和为dis。 假设good点不止一个&#xff0c;那么我们good点的dis应该都是相等的&#xff08;废话&#xff09;。设当前点u是good点&#xff0c;如果他往儿子v移动&#xff0c;儿子有w个点属于k&#…
阅读更多...
Maven 项目模板学习

Maven 项目模板学习

目录 Maven 项目模板 什么是 archetype&#xff1f; 使用项目模板 Maven 将询问原型的版本 创建的项目 创建 pom.xml Maven 项目文档 Maven 快照(SNAPSHOT) 什么是快照? 项目快照 vs 版本 app-ui 项目的 pom.xml 文件 Maven 快照(SNAPSHOT)的出现是因为为了如果pom有…
阅读更多...
OpenPCDet系列 | 4.4 DataProcessor点云数据处理模块解析

OpenPCDet系列 | 4.4 DataProcessor点云数据处理模块解析

文章目录 DataProcessor模块解析1. mask_points_and_boxes_outside_range2. shuffle_points3. transform_points_to_voxels DataProcessor模块解析 在对batch_data的处理中&#xff0c;经过了point_feature_encoder模块处理后&#xff0c;就轮到了进行data_processor处理。在d…
阅读更多...
django路由（多应用配置）

django路由（多应用配置）

一、配置全局路由 在应用下&#xff0c;定义视图函数views.py from django.http import HttpResponse from django.shortcuts import render# Create your views here.def get_order(request):return HttpResponse("orders应用下的路由") 在项目的urls路由配置中&…
阅读更多...
Qt事件传递及相关的性能问题

Qt事件传递及相关的性能问题

在使用Qt时&#xff0c;我们都知道能通过mousePressEvent&#xff0c;eventFilter等虚函数的重写来处理事件&#xff0c;那么当我们向一个界面发送事件&#xff0c;控件和它的父控件之间的事件传递过程是什么样的呢&#xff1f; 本文将以下图所示界面为例&#xff0c;结合源码介…
阅读更多...
【sentinel】热点规则详解及源码分析

【sentinel】热点规则详解及源码分析

何为热点&#xff1f;热点即经常访问的数据。很多时候我们希望统计某些热点数据中访问频次最高的Top K数据&#xff0c;并对其访问进行限制。 比如&#xff1a; 商品ID为参数&#xff0c;统计一段时间内最常购买的商品ID并进行限制用户ID为参数&#xff0c;针对一段时间内频繁…
阅读更多...
【linux】init进程的详解

【linux】init进程的详解

文章目录 概述init进程完成从内核态向用户态的转变&#xff08;1&#xff09;一个进程先后两种状态&#xff08;2&#xff09;init进程在内核态下的工作内容&#xff08;3&#xff09;init进程在用户态下的工作内容&#xff08;4&#xff09;init进程如何从内核态跳跃到用户态 …
阅读更多...
springboot+vue高校社团管理系统（源码+文档）

springboot+vue高校社团管理系统（源码+文档）

风定落花生&#xff0c;歌声逐流水&#xff0c;大家好我是风歌&#xff0c;混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的高校社团管理系统。项目源码以及部署相关请联系风歌&#xff0c;文末附上联系信息 。 &#x1f495;&#x1f495;作者&#xff1a;风…
阅读更多...
Linux快速安装Erlang和RabbitMQ单机版

Linux快速安装Erlang和RabbitMQ单机版

环境 CentOS7Xshell6XFtp6Erlang 21.3RabbitMQ 3.8.4 安装方式 同一个软件有很多种安装方式&#xff0c;在Linux系统有几种常见的软件安装方式&#xff1a; 源码编译安装&#xff1a;一般需要解压&#xff0c;然后使用make、make install等命令RPM&#xff08;RedHat Packa…
阅读更多...
从物业管理到IT互联网精英，月薪11k的她几经辗转，终得偿所愿！

从物业管理到IT互联网精英，月薪11k的她几经辗转，终得偿所愿！

所谓“男怕入错行”&#xff0c;其实对女生来说也是一样&#xff0c;不同行业对人生的改变太大&#xff0c;想要找到满意的工作&#xff0c;就要不断去尝试。 西安的学员小文&#xff0c;大学毕业后从事的本专业&#xff08;物业管理&#xff09;工作&#xff0c;但不是很喜欢…
阅读更多...
条款1：理解模板类型推导

条款1：理解模板类型推导

现代C中被广泛应用的auto是建立在模板类型推导的基础上的。而当模板类型推导规则应用于auto环境时&#xff0c;有时不如应用于模板中那么直观。由于这个原因&#xff0c;真正理解auto基于的模板类型推导的方方面面非常重要。 在c中声明一个模板函数的伪代码基本如下&#xff1…
阅读更多...
JVM 直接内存(Direct Memory)

JVM 直接内存(Direct Memory)

直接内存概述 不是虚拟机运行时数据区的一部分&#xff0c;也不是<<Java 虚拟机规范>> 中定义的内存区域直接内存是Java 堆外的、直接向系统申请的内存区间来源于 NIO&#xff0c;通过存在堆中的 DirectByteBuffer 操作 Native 内存访问直接内存的速度会优于 Java…
阅读更多...
智慧停车APP系统开发 停车取车缴费智能搞定

智慧停车APP系统开发 停车取车缴费智能搞定

生活水平的提高让车辆成为很多人出行主要的代步工具&#xff0c;很多家庭现在已经不止拥有一辆汽车了&#xff0c;所以城市建设中关于停车场的规划管理也是很重要的部分。不过现在出门很多时候还是会碰到找不到停车场&#xff0c;没有车位、收费不合理、乱收费等现象。智慧停车…
阅读更多...
调试和优化遗留代码

调试和优化遗留代码

1. 认识调试器 1.1 含义 一个能让程序运行、暂停、然后对进程的状态进行观测甚至修改的工具。 在日常的开发当中使用非常广泛。(PHP开发者以及前端开发者除外) 1.2 常见的调试器 Go语言的自带的 delve 简写为 “dlv”GNU组织提供的 gdbPHP Xdebug前端浏览器debug 调试 1.3…
阅读更多...
DNS投毒

DNS投毒

定义 DNS缓存投毒又称DNS欺骗，是一种通过查找并利用DNS系统中存在的漏洞，将流量从合法服务器引导至虚假服务器上的攻击方式。与一般的钓鱼攻击采用非法URL不同的是，这种攻击使用的是合法URL地址。 DNS缓存中毒如何工作 在实际的DNS解析过程中，用户请求某个网站，浏览器首…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023