Problem - D2 - Codeforces
Problem - D2 - Codeforces
思路:
我们设good点到所有k点的距离和为dis。
- 假设good点不止一个,那么我们good点的dis应该都是相等的
(废话)。 - 设当前点u是good点,如果他往儿子v移动,儿子有w个点属于k,那么v的距离和是dis-w+(k-w)=dis+k-2w(即往儿子走,儿子子树里w个点到当前点的距离减一,子树外面的点距离+1)
- 因为u是good点,所以k-2w>=0
- 如果存在其他good点,我们显然每次走都应该是等号成立
- 你会发现,k为奇数时k/2!=w。所以k为奇数,显然只有应该good点,任何分布情况都是k为1.
- 当满足k/2=w,即v的子树有k/2个点,子树外面有k/2个点,便是good点。
- 发现每次移动都是等号成立,即good点应该是连成一片的。(而且我们保证,任何分布情况至少2个good点。因为那两颗有k/2个点是目标点的子树,他们的根节点必然就是good点)
- 我们dfs确认符合思路3的边(即good之间的边)。那么符合条件的点就是符合的边+1
- 为什么不直接算点呢?
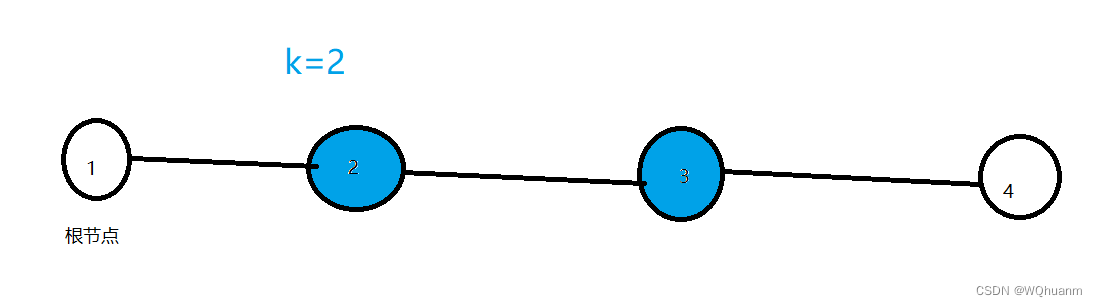
- 如上图,我们从1遍历,2,3显然是good点,但是这样从根节点遍历2却不是,因为他的子树是(2-3-4),有3个点,而如果他的子树是(2-1),那么就是good点。
- 即我们dfs实际遍历的是符合条件的点之间的边(如这里成功计算的就是2-3的边)。
- 所以我们任何分布情况都计算了一个点
- 那么答案就是(ΣC(sz[v],k/2)*C(n-sz[v],k/2)/C(n,k) )+1,即每个点的期望就是,所以可能的分布C(n,k)下,子树内部选k/2个点,外面选k/2个点的情况,最后加上任何情况都漏下的一个点
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
const int N = 3e5 + 10;
const int mod=1e9+7;
int n,k;
vector<int>edge[N];
int pre[N],inv[N],sz[N];
ll ans;
ll fastmi(ll base,ll power)
{
ll ans=1;
while(power)
{
if(power&1)ans=ans*base%mod;
base=base*base%mod;
power>>=1;
}
return ans;
}
int C(int n,int m)
{
if(n<0||m<0||n<m)return 0;
return pre[n]*inv[m]%mod*inv[n-m]%mod;//取模运算不允许出现除法,所以除数都转化为逆元存下来
}
void dfs(int u,int f)
{
sz[u]=1;
for(auto v:edge[u])if(v!=f)
{
dfs(v,u);
sz[u]+=sz[v];
ans=(ans+C(sz[v],k/2)*C(n-sz[v],k/2)%mod)%mod;//计算子树v的贡献
}
}
void mysolve()
{
cin>>n>>k;
int x,y;
for(int i=1; i<n; ++i)cin>>x>>y,edge[x].push_back(y),edge[y].push_back(x);
if(k&1)
{
cout<<1<<endl;
return;
}
ans=C(n,k);//即+1
dfs(1,0);
ans=ans*fastmi(C(n,k),mod-2)%mod;
cout<<ans<<endl;
return;
}
int32_t main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
ll t=1;
//cin >> t;
pre[0]=1;
for(int i=1; i<=2e5; ++i)pre[i]=pre[i-1]*i%mod;
inv[200000]=fastmi(pre[200000],mod-2);
for(int i=2e5-1; ~i; --i)inv[i]=inv[i+1]*(i+1)%mod;
//for(int i=)
while (t--)
{
mysolve();
}
system("pause");
return 0;
}