MD-MTSP：孔雀优化算法POA求解多仓库多旅行商问题（提供MATLAB代码，可以修改旅行商个数及起点）

news2025/1/24 4:55:12

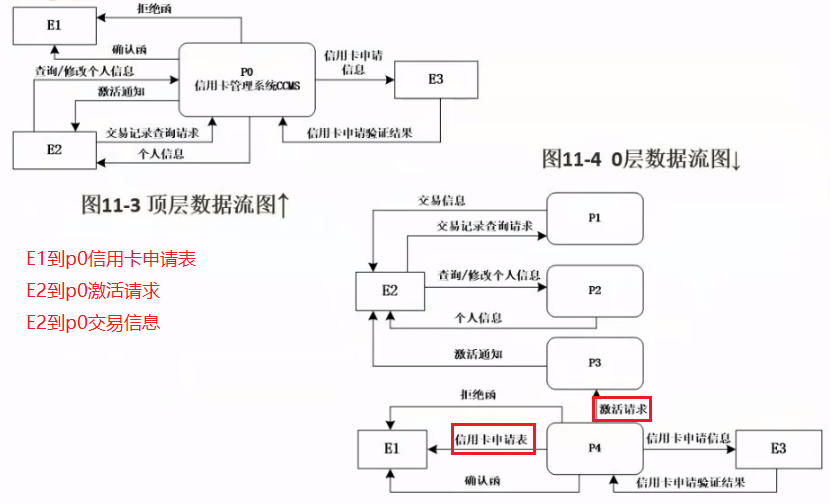
一、多仓库多旅行商问题

多旅行商问题（Multiple Traveling Salesman Problem, MTSP）是著名的旅行商问题（Traveling Salesman Problem, TSP）的延伸，多旅行商问题定义为：给定一个𝑛座城市的城市集合，指定𝑚个推销员，每一位推销员从起点城市出发访问一定数量的城市，最后回到终点城市，要求除起点和终点城市以外，每一座城市都必须至少被一位推销员访问，并且只能访问一次，需要求解出满足上述要求并且代价最小的分配方案，其中的代价通常用总路程长度来代替，当然也可以是时间、费用等。多仓库多旅行商问题是其中一种多旅行商问题。

多仓库多旅行商问题（Multi-Depot Multiple Travelling Salesman Problem, MD-MTSP）：𝑚个推销员从𝑚座不同的城市出发，访问其中一定数量的城市并且每座城市只能被某一个推销员访问一次，最后回到各自出发的城市，这种问题模型被称之为MD-MTSP。

二、孔雀优化算法POA

孔雀优化算法 ( Peafowl Optimization Algorithm, POA), 是由 Jingbo Wang 等于2022 年提出的一种群体智能优化算法。其灵感来源于孔雀的群体行为。

孔雀优化算法POA提供MATLAB代码

三、孔雀优化算法POA求解多仓库多旅行商问题MDMTSP

MDMTSP：孔雀优化算法POA求解多仓库多旅行商问题
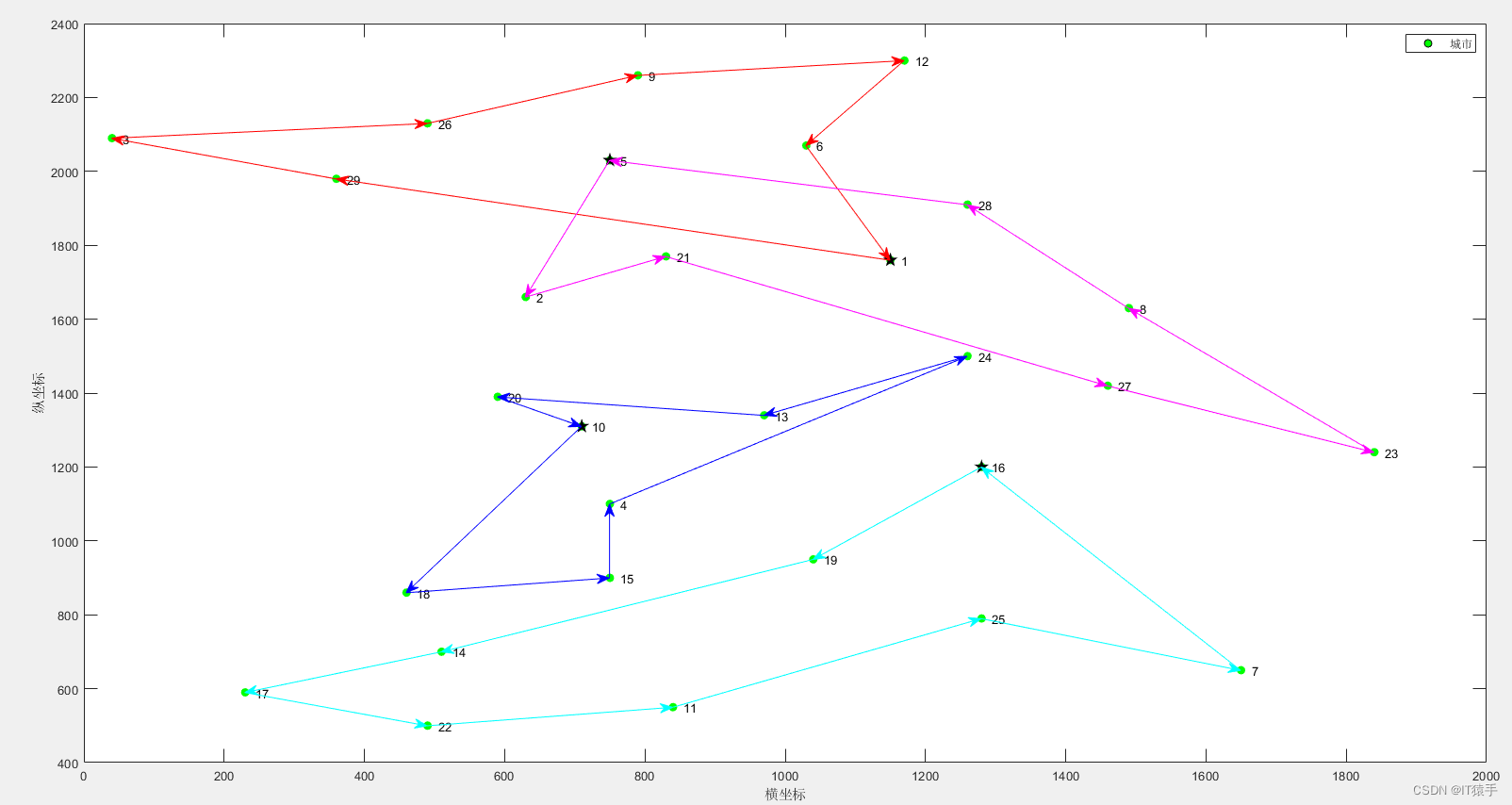
本文选取国际通用的TSP实例库TSPLIB中的测试集bayg29，bayg29中城市分布如下图所示：
在这里插入图片描述

以四个旅行商为例，部分代码如下：可以修改旅行商个数及起点

完整MATLAB code link ：https://mbd.pub/o/bread/ZJmTlJxp

close all
clear
clc
global data  StartPoint Tnum
%数据集参考文献  REINELT G.TSPLIB-a traveling salesman problem[J].ORSA Journal on Computing,1991,3(4):267-384.
% 导入TSP数据集 bayg29
load('data.txt')
StartPoint=[1 5 10 16];%起点城市的序号(可以修改) 必须由小到大排列 （建议：2到6个旅行商）
Tnum=length(StartPoint);%旅行商个数
Dim=size(data,1)-Tnum;%维度
lb=-100;%下界
ub=100;%上界
fobj=@Fun;%计算总距离
SearchAgents_no=50; % 种群大小（可以修改）
Max_iteration=2000