1.堆排序

堆排序即利用堆的思想来进行排序

升序：建大堆
降序：建小堆

1.1向上调整和向下调整建堆对比

上一篇文章我们讲了建堆的接口，咱么用的是向下调整建堆，那为什么不用向上调整建堆呢？下面我们就来对比一下那种方法更优

向上调整建堆时间复杂度图解：

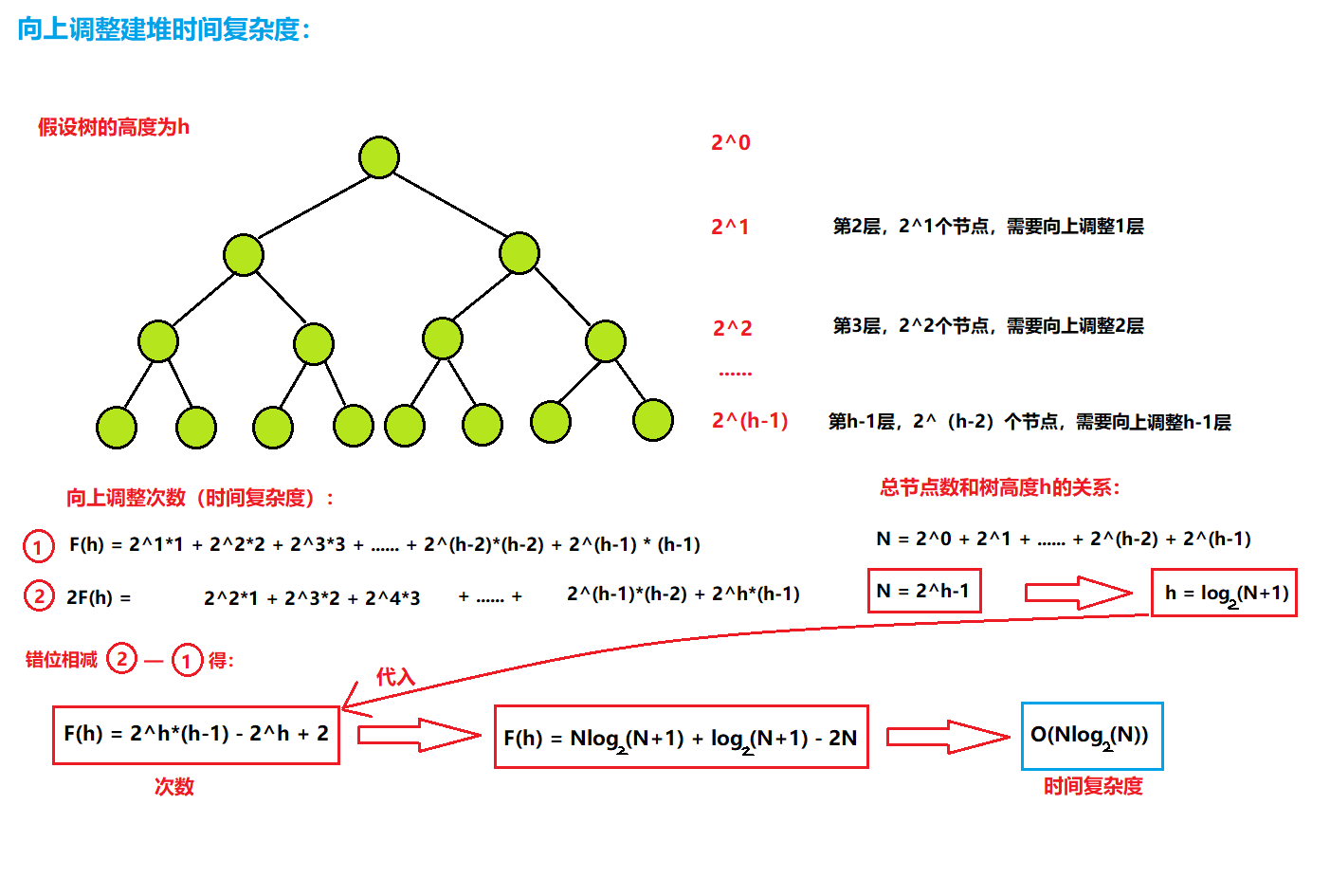
向下调整建堆时间复杂度图解：

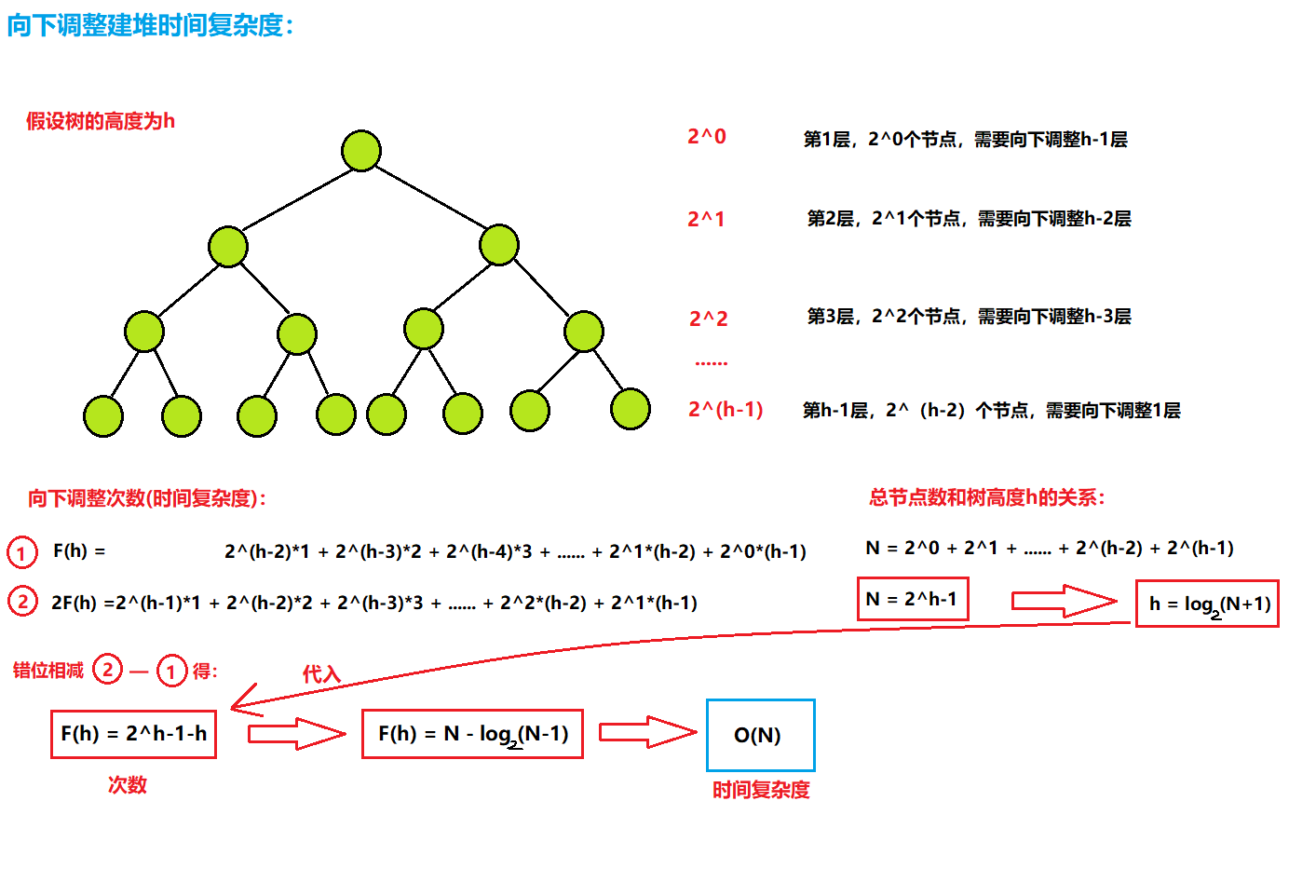
由图解我们得到结论：
向上调整建堆的时间复杂度为：O(N*log₂(N))；向下调整建堆的时间复杂度为：O(N)

1.2堆排序实现

1.2.1升序

升序，建大堆
首先交换堆的首尾数据，把最大的数放在尾部，再从根节点开始向下调整size-1个数据（递减：从size-1开始每放一个数据就 -1，也就是不对交换到尾部的元素进行调整）

//交换函数
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向下调整（建大堆）
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//假定左孩子
	while (child < n)
	{
		//大堆：保证child指向大的那个孩子
		if (a[child + 1] > a[child] && child + 1 < n)
		{
			child++;
		}
		//大堆：孩子大于父亲就交换，并继续向下比较调整，反之则调整结束
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//堆排序
//升序：建大堆
void HeapSort(int* a, int n)
{
	//建堆算法
	//从最后一个元素的父节点开始依次向前可以遍历到每颗子树的父节点
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		//交换首尾数据
		Swap(&a[0], &a[end]);
		//从首元素开始向下调整
		AdjustDown(a, end, 0);
		--end;
	}
}

1.2.2降序

降序，建小堆
首先交换堆的首尾数据，把最小的数放在尾部，再从根节点开始向下调整size-1个数据（递减：从size-1开始每放一个数据就 -1，也就是不对交换到尾部的元素进行调整）

//交换函数
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向下调整（建小堆）
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//假定左孩子
	while (child < n)
	{
		//小堆：保证child指向小的那个孩子
		if (a[child + 1] < a[child] && child + 1 < n)
		{
			child++;
		}
		//小堆：孩子小于父亲就交换，并继续向下比较调整，反之则调整结束
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//堆排序
//降序：建小堆
void HeapSort(int* a, int n)
{
	//建堆算法
	//从最后一个元素的父节点开始依次向前可以遍历到每颗子树的父节点
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		//交换首尾数据
		Swap(&a[0], &a[end]);
		//从首元素开始向下调整
		AdjustDown(a, end, 0);
		--end;
	}
}

2.Top-K问题

什么是Top-K问题？

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大
比如：专业前10名、世界500强、富豪榜、游戏中战力前100的玩家等

2.1解决思路

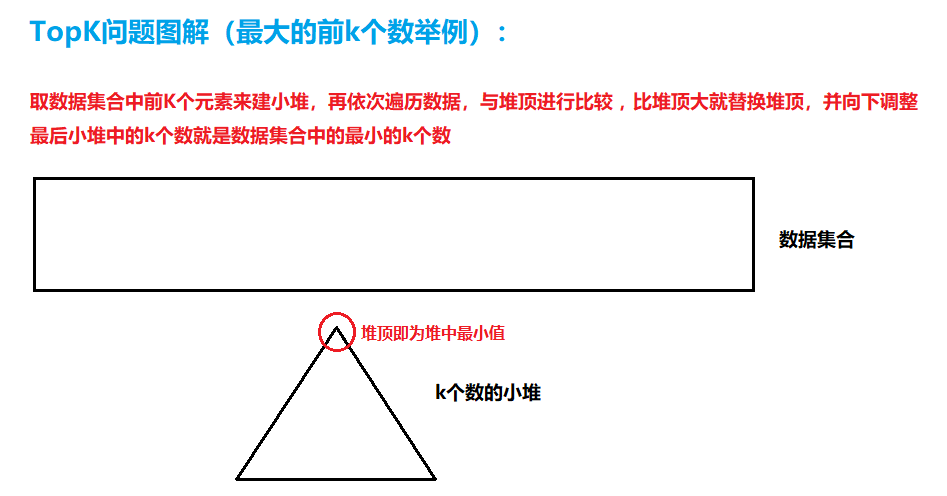
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

1.用数据集合中前K个元素来建堆

前k个最大的元素，则建小堆
前k个最小的元素，则建大堆

2.用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素

2.2代码实现

根据上面的思路，来举两个栗子

1.求有10000个数据的数组中最大的10个数

//Top-K问题
void Topk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand(time(0));
	//使数组中的数都在1000000以内
	for (size_t i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
	//手动设置10个大于1000000的数
	a[12] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 1000000 + 5;
	a[2335] = 1000000 + 6;
	a[9999] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[3144] = 1000000 + 10;
	//将数组a中前k个数据读到数组minHeap中
	int k = 10;
	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}
	for (int i = 0; i < k; ++i)
	{
		a[i] = minHeap[i];
	}
	//建一个k个大小的小堆minHeap
	for (int h = (k - 1 - 1) / 2; h >= 0; --h)
	{
		AdjustDown(minHeap, k, h);
	}
	//遍历数组中的剩余数与堆顶比较，大于则替换并向下调整
	for(int j = k;j < n; ++j)
	{
		if (a[j] > minHeap[0])
		{
			minHeap[0] = a[j];
			AdjustDown(minHeap, k, 0);
		}
	}
	//打印小堆数据即为数组a中最大的10个数
	for (int g = 0; g < k; ++g)
	{
		printf("%d ", minHeap[g]);
	}
	printf("\n");
}

2.从文件中读取数据求最大的前k的

//Top-K问题
void Topk()
{
	//写数据到文件中
	int n, k;
	printf("请输入在n个数中选取最大的k个数:>");
	scanf("%d%d", &n, &k);
	srand(time(0));
	FILE* fin = fopen("data.txt", "w");
	if (fin == NULL)
	{
		perror("fopen fail");
		return;
	}
	for (size_t i = 0; i < n; ++i)
	{
		int val = rand();
		fprintf(fin, "%d\n", val);
	}
	fclose(fin);

	//找topk
	FILE* fout = fopen("data.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}
	//开辟k个大小的数组
	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}
	//将文件中的前k个数据读到数组中
	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	//建一个k个大小的小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(minHeap, k, i);
	}
	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{
		if (val > minHeap[0])
		{
			minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}
	for (int i = 0; i < k; ++i)
	{
		printf("%d ", minHeap[i]);
	}
	printf("\n");

	fclose(fout);
}