- 博主简介:想进大厂的打工人
- 博主主页:@xyk:
- 所属专栏: 笔试强训专栏
深度优先遍历(Depth First Search, 简称 DFS) 与广度优先遍历(Breath First Search)是图论中两种非常重要的算法。
本文就以习题的方式来给大家讲解 DFS 和 BFS
目录
文章目录
一、DFS与BFS
1.1 DFS 概念
1.2 BFS 概念
DFS代码一般为
BFS代码一般为
二、[编程题]红与黑
三、[编程题]走迷宫
四、[编程题]五子棋
一、DFS与BFS
1.1 DFS 概念
深度优先遍历主要思路是从图中一个未访问的顶点 V 开始,沿着一条路一直走到底,然后从这条路尽头的节点回退到上一个节点,再从另一条路开始走到底…
不断递归重复此过程,直到所有的顶点都遍历完成,它的特点是不撞南墙不回头,先走完一条路,再换一条路继续走。
简单来说,就是一条路走到头,走不动为止,再回头重新走
DFS代码一般为:
- 递归出口
- 标记当前位置
- 递归找下一个
- 回溯(将之前标记的位置还原)
1.2 BFS 概念
广度优先遍历,指的是从图的一个未遍历的节点出发,先遍历这个节点的相邻节点,再依次遍历每个相邻节点的相邻节点。
放到树的遍历中而言,就是层序遍历(levelorder)。
因为需要保存相邻节点,所以我们需要使用到队列(queue)这个数据结构,由于其具有先入先出的特性,就可以遍历完一层又遍历下一层。
简单来说,就是走一步看一步,走一步之后再去走其他路,直到走完
BFS代码一般为
- 初始状态入队
- 只要队列不为空
2.1 取队头元素
2.2 扩展队列
不多坠述,用习题来讲解
二、[编程题]红与黑
红与黑__牛客网 (nowcoder.com)
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的(上下左右四个方向)黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。


做法一:DFS深度优先遍历
思路:
本题让我们计算能够到达多少块黑色的瓷砖,那么首先就应该想到(DFS)深度优先遍历,因为一条道走到黑并统计黑色瓷砖,直到遇到白色瓷砖,回溯回去并换一条路再次走到黑~~~
首先我们要找到 @ 起点位置,然后进行 DFS ,每走到一个位置就标记为 true
本题不需要将标记还原!!!
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
/**
* @author xyk的电脑
* @version 1.0
* @description: TODO
* @date 2023/5/9 20:13
*/
public class Main {
static boolean[][] flag;
static int ans = 0;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()){
int row = scanner.nextInt();
int col = scanner.nextInt();
int m = 0;
int n = 0;
ans = 0;
flag = new boolean[row][col];
char[][] map = new char[row][col];
for (int i = 0; i < row; i++) {
String str = scanner.next();
for (int j = 0; j < col; j++) {
map[i][j] = str.charAt(j);
flag[i][j] = false;
if (map[i][j] == '@'){//起点位置
m = i;
n = j;
}
}
}
dfs(map,m,n);
System.out.println(ans);
}
}
private static void dfs(char[][] map, int m, int n) {
if (m >= map.length || n >= map[0].length
|| m < 0 || n < 0 ){//越界
return;
}
if (map[m][n] == '#' ){//如果是白色瓷砖 不可以走
return;
}
if (flag[m][n]){//如果已经走过了
return;
}
ans++; //四个路径之和
flag[m][n] = true;
dfs(map,m + 1,n);
dfs(map,m,n + 1);
dfs(map,m - 1,n);
dfs(map,m,n - 1);
}
}做法二:BFS 广度优先遍历
在BFS中,应用 队列 来存储结点,首先将起点存入,然后再存入起点的旁边的四个结点,然后再依次取出其他的结点,来进行遍历,每次走到一个结点后,count++ 一次来统计黑色的瓷砖
总结来说,就是走到一个结点后,存储周围的结点,并且标记,然后循环这个步骤一直到队列为空
class Main2{
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()){
int m = scanner.nextInt();
int n = scanner.nextInt();
Character[][] map = new Character[m][n];
Node start = null;
for (int i = 0; i < m; i++) {
String s = scanner.next();
for (int j = 0; j < n; j++) {
map[i][j] = s.charAt(j);
if (s.charAt(j) == '@'){
start = new Node(i,j);
}
}
}
int[][] direction = {{0,1},{0,-1},{1,0},{-1,0}};
bfs(map,direction,start);
}
}
private static void bfs(Character[][] map, int[][] direction, Node start) {
Queue<Node> queue = new LinkedList<>();
boolean[][] visited = new boolean[map.length][map[0].length];
queue.add(start);
visited[start.x][start.y] = true;
int count = 1;
while (!queue.isEmpty()){
Node cur = queue.poll();
for (int i = 0; i < 4; i++) {
Node next = new Node(cur.x + direction[i][0], cur.y + direction[i][1]);
if (next.x >=0 && next.x < map.length && next.y >= 0 && next.y < map[0].length
&& map[next.x][next.y] != '#'
&& !visited[next.x][next.y]){
count++;
queue.add(next);
visited[next.x][next.y] = true;
}
}
}
System.out.println(count);
}
static class Node{
int x;
int y;
public Node(int x,int y){
this.x = x;
this.y = y;
}
}
}
三、[编程题]走迷宫
走迷宫__牛客网 (nowcoder.com)
NowCoder最喜欢游乐场的迷宫游戏,他和小伙伴们比赛谁先走出迷宫。
现在把迷宫的地图给你,你能帮他算出最快走出迷宫需要多少步吗?


本题应用DFS+动态规划 或者 BFS,因为求的是最短路径
个人认为这道题用BFS效率高些,与DFS相比因为没有使用递归反复更新格子里的值
由于求的是最短路径,所以要进行回溯再次计算,不用标记为 true
做法一:DFS 深度优先遍历


注意 dp[x][y] = Math.min(dp[i][j] + 1, dp[x][y])
class Main4 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
char[][] str = new char[10][10];
int[][] dp = new int[10][10];
while (scanner.hasNext()) {
for (int i = 0; i < 10; i++) {
String ret = scanner.next();
for (int j = 0; j < 10; j++) {
str[i][j] = ret.charAt(j);
dp[i][j] = Integer.MAX_VALUE;
}
}
dp[0][1] = 0;
dfs(str, 0, 1, dp);
System.out.println(dp[9][8]);
}
}
private static void dfs(char[][] str, int i, int j, int[][] dp) {
//i j坐标不是终点
int[][] pos = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};//有四个方向 上下左右
for (int k = 0; k < 4; k++) {//控制点的四个方向
// 沿着一个树的分支 走到终点
int x = i + pos[k][0];
int y = j + pos[k][1];
if (x >= 0 && x < 10 && y >= 0 && y < 10
&& str[x][y] == '.' && dp[x][y] > dp[i][j] + 1) {
//不越界 并且是通路 并且没有到达过
// 如果说已经dp[x][y]已经是从入口到达(x,y)的最短路径了 就不需要从这个点开始找寻最短路径了 因为这个点已经在最短路径之中了
//如果某一个路径经过这个点的距离更小,这个路径才有可能会是最短路径
dp[x][y] = Math.min(dp[i][j] + 1, dp[x][y]);
if (x == 9 && y == 8) {
return;//找到了其中一个路径 回溯 dp[x][y]保留路径的最终长度
}
dfs(str, x, y, dp);//沿着一个树的分支 走到终点
//递归结束之后 回溯 在for循环的控制下 找到新的路径
}
}
}
}做法二:BFS 广度优先遍历
二叉树的层次遍历,从根节点到指定叶子节点 的层数

class Note {
int x;
int y;
public Note(int x, int y) {
this.x = x;
this.y = y;
}
}
class Main5 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
char str[][] = new char[10][10];
while (scanner.hasNext()) {
for (int i = 0; i < 10; i++) {
String ret = scanner.next();
for (int j = 0; j < 10; j++) {
str[i][j] = ret.charAt(j);
}
}
System.out.println(bfs(str));
}
}
private static int bfs(char[][] str) {
Queue<Note> queue = new LinkedList();
boolean flag[][] = new boolean[10][10];//用于标识元素是否已经被使用
int max = 0;
int[][] pos = {{1, 0}, {0, 1}, {0, -1}, {-1, 0}};//有四个方向 上下左右
//第一层 放入根
Note note = new Note(0, 1);
queue.add(note);
flag[0][1] = true;
while (!queue.isEmpty()) {
int size = queue.size();
while (size-- > 0) {
note = queue.poll();
//存入这个结点 可以下 右 左 上到的移动的位置
int x = note.x;
int y = note.y;
if (x == 9 && y == 8)///最后从队列取得元素 是出口就结束了
return max;
flag[x][y] = true;//得到 这层元素的下一层元素 这个结点已经被使用
for (int i = 0; i < 4; ++i) {//控制四个方向
int posi = x + pos[i][0];
int posj = y + pos[i][1];
if (posi >= 0 && posi <= 9 && posj >= 0 && posj <= 9 && !flag[posi][posj] && str[posi][posj] == '.') {
Note note1 = new Note(posi, posj);
queue.add(note1);
}
}
}
//统计完一层结点的下一个位置 也就是获取了一层元素
max++;
}
return max;
}
}四、[编程题]五子棋
五子棋__牛客网 (nowcoder.com)
NowCoder最近爱上了五子棋,现在给你一个棋局,请你帮忙判断其中有没有五子连珠(超过五颗也算)。

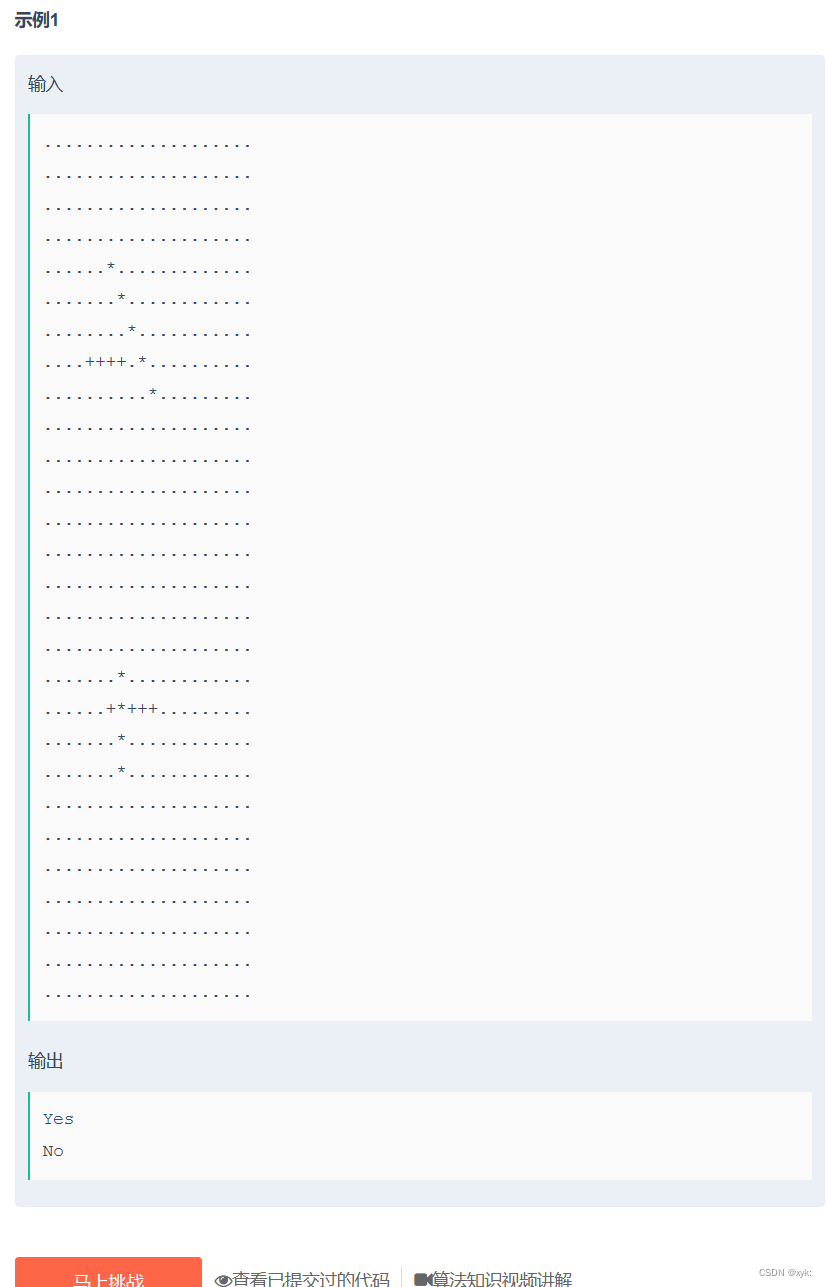
本题类似于 DFS,但是不需要递归,只需要判断八个方向的能否连上即可
public class Main {
//八个位置
static int[][] direction = {{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,-1},{1,-1},{-1,1}};
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()){
Character[][] map = new Character[20][20];
for (int i = 0; i < 20; i++) {
String s = scanner.next();
for (int j = 0; j < 20; j++) {
map[i][j] = s.charAt(j);
}
}
if (check(map)){
System.out.println("Yes");
}else {
System.out.println("No");
}
}
}
private static boolean check(Character[][] map) {
for (int i = 0; i < 20; i++) {
for (int j = 0; j < 20; j++) {
if (map[i][j] == '*' || map[i][j] == '+'){
for (int k = 0; k < 8; k++) {
int count = 1;
int x = i + direction[k][0];
int y = j + direction[k][1];
while (x >= 0 && x < 20 && y >= 0 && y < 20
&& map[i][j] == map[x][y]){
count++;
x += direction[k][0];
y += direction[k][1];
}
if (count == 5){
return true;
}
}
}
}
}
return false;
}
}