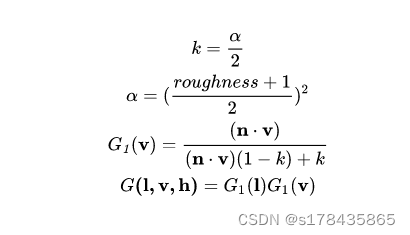利用这些假设（局部光学平坦表面，没有相互反射），可以很容易推导出一个被称为Microfacet Cook-Torrance BRDF的一般形式的Specular BRDF项。此Specular BRDF具有以下形式：

 

其中：

• D(h) : 法线分布函数 （Normal Distribution Function），描述微面元法线分布的概率，即正确朝向的法线的浓度。即具有正确朝向，能够将来自l的光反射到v的表面点的相对于表面面积的浓度。
• F(l,h) : 菲涅尔方程（Fresnel Equation），描述不同的表面角下表面所反射的光线所占的比率。
• G(l,v,h) : 几何函数（Geometry Function），描述微平面自成阴影的属性，即m = h的未被遮蔽的表面点的百分比。
• 分母 4(n·l)(n·v）：校正因子（correctionfactor），作为微观几何的局部空间和整个宏观表面的局部空间之间变换的微平面量的校正。

关于Cook-Torrance BRDF，需要强调的两点注意事项：

• 对于分母中的点积，仅仅避免负值是不够的 ,也必须避免零值。通常通过在常规的clamp或绝对值操作之后添加非常小的正值来完成。
• Microfacet Cook-Torrance BRDF是实践中使用最广泛的模型，实际上也是人们可以想到的最简单的微平面模型。它仅对几何光学系统中的单层微表面上的单个散射进行建模，没有考虑多次散射，分层材质，以及衍射。Microfacet模型，实际上还有很长的路要走。

Specular D

描述微面元法线分布的概率，即正确朝向的法线的浓度。即具有正确朝向，能够将来自l的光反射到v的表面点的相对于表面面积的浓度。

法线分布函数（Normal Distribution Function, NDF）D的常见模型可以总结如下：

• Beckmann[1963]
• Blinn-Phong[1977]
• GGX [2007] / Trowbridge-Reitz[1975]
• Generalized-Trowbridge-Reitz(GTR) [2012]
• Anisotropic Beckmann[2012]
• Anisotropic GGX [2015]

其中，业界较为主流的法线分布函数是GGX（Trowbridge-Reitz），因为具有更好的高光长尾：

 

另外，需要强调一点。Normal Distribution Function正确的翻译是法线分布函数，而不是正态分布函数。google翻译等翻译软件会将Normal Distribution Function翻译成正态分布函数，而不少中文资料就跟着翻译成了正态分布函数，这是错误的。

其实，一些参考文献会使用术语“法线分布(distribution of normals)”来避免与高斯正态分布(Gaussian normal distribution)混淆。

Specular F

描述不同的表面角下表面所反射的光线所占的比率。

对于菲涅尔（Fresnel）项，业界方案一般都采用Schlick的Fresnel近似，因为计算成本低廉，而且精度足够：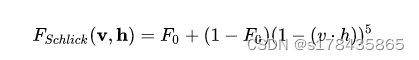

 

菲涅尔项的常见模型可以总结如下：

• Cook-Torrance [1982]
• Schlick [1994]
• Gotanta [2014]

Specular G

描述微平面自成阴影的属性，即m = h的未被遮蔽的表面点的百分比。

几何项G的常见模型可以总结如下：

• Smith [1967]
• Cook-Torrance [1982]
• Neumann [1999]
• Kelemen [2001]
• Implicit [2013]

另外，Eric Heitz在[Heitz14]中展示了Smith几何阴影函数是正确且更准确的G项，并将其拓展为Smith联合遮蔽阴影函数（Smith Joint Masking-Shadowing Function），该函数具有四种形式：

• 分离遮蔽阴影型（Separable Masking and Shadowing）
• 高度相关掩蔽阴影型（Height-Correlated Masking and Shadowing）
• 方向相关掩蔽阴影型（Direction-Correlated Masking and Shadowing）
• 高度-方向相关掩蔽阴影型（Height-Direction-Correlated Masking and Shadowing）

目前较为常用的是其中最为简单的形式，分离遮蔽阴影（Separable Masking and Shadowing Function）。

该形式将几何项G分为两个独立的部分：光线方向（light）和视线方向（view），并对两者用相同的分布函数来描述。根据这种思想，结合法线分布函数（NDF）与Smith几何阴影函数，于是有了以下新的Smith几何项：

• Smith-GGX
• Smith-Beckmann
• Smith-Schlick
• Schlick-Beckmann
• Schlick-GGX

其中UE4的方案是上面列举中的“Schlick-GGX”，即基于Schlick近似，将k映射为 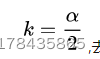,去匹配GGX Smith方程：

 

 

---