目录
一、二叉排序树(BST)
查询
插入
构造二叉排序树
*删除
*查找效率分析
二、二叉平衡树
*插入数据保持平衡
LL
编辑
RR
LR
RL
结
*查找效率分析
删除
三、红黑树
*插入
*删除
四、B树
*插入
*删除
五、B+树
一、二叉排序树(BST)
定义:二叉排序树(也称二叉查找树)或者是一颗空树,或者是具有下列特性的二叉树:
1)若左子树非空,则左子树上所有结点的值均小于根的值
2)若右子树非空,则左右子树上所有结点的值均小于根的值
3)左右子树也分别是一颗二叉排序树
左子树值<根结点值<右子树值
type struct BSTNode{
int key;
struct BSTNode *lchild,*rchild;
}BSTNode,*BSTree;
查询
非递归方法
BSTNode *BST_Search(BSTree T,int key){
while(T!=NULL && key!=t->key){
if(key<T->key)
T=T->lchild; //小则左子树查找
else
T=T->rchild; //大则右子树查找
}
return T;
}递归方法实现
BSTNode *BSTSearch(BSTree T,int key){
if(T==NULL) return NULL;
if(key == T->key)
return T;
else if(key<T->key)
BSTSearch(T->lchild,key);
else
BSTSearch(T->rchild,key);
}插入
int BST_Insert(BSTree &T,int k){
if(T==NULL){
T=(BSTree)malloc(sizeof(NSTNode));
T->key=k;
T->lchild=T->rchild=NULL;
return 1; //返回1,插入成功
}else if(k==T->key){
return 0; //返回0,已有,插入失败
}else if(k<T->key)
return BST_Insert(T->lchild); //插入到T的左子树
else
retunr BST_Insert(T->rchild); //插入到T的右子树
}构造二叉排序树
不同的关系中序列顺序可能的到不同二叉排序树
void Creat_BST(BSTree &T,int str[],int n){
T=NULL;
int i=0;
while(i<n){
BST_Insert(T,str[i]);
i++;
}
}*删除
①若被删除的z结点是叶结点,则直接删除,不会破坏二叉排序树的性质
②若z结点只有一颗左子树或者右子树,则让z的子树成为z的父结点的子树,替代z的位置
③若结点z有左右两课子树,则令z的直接后继(或者直接前驱)代替z,然后从二叉排序树中删除这个直接后继(或者直接前驱),这样就转换成了第一或第二情况
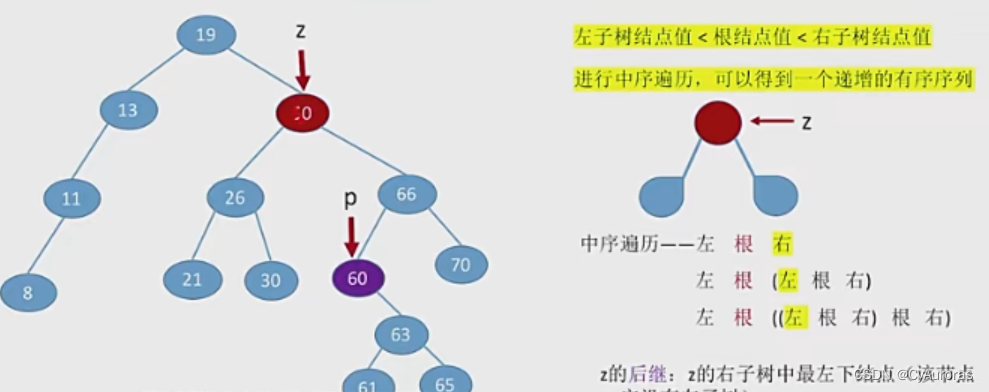
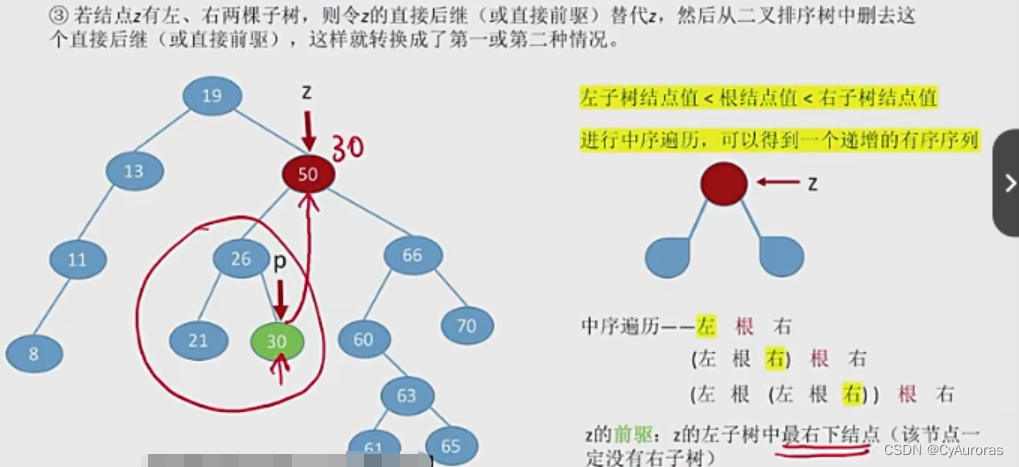
*查找效率分析
查找成功:
成功=(第几层*每层成功结点树)累和/总成功结点数
(折半查找一样计算)
查找失败:
失败=(失败的层*每层数量)累和/总失败结点数(折半查找一样计算)
二、二叉平衡树
定义:二叉平衡树,简称平衡树(AVL树) ,树上任意一结点的左子树和右子树的高度之差不超过1
结点的平衡因子=左子树高-右子树高

typedef struct AVLNode{
int key; //数据域
int balance; //平衡因子
struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;*插入数据保持平衡


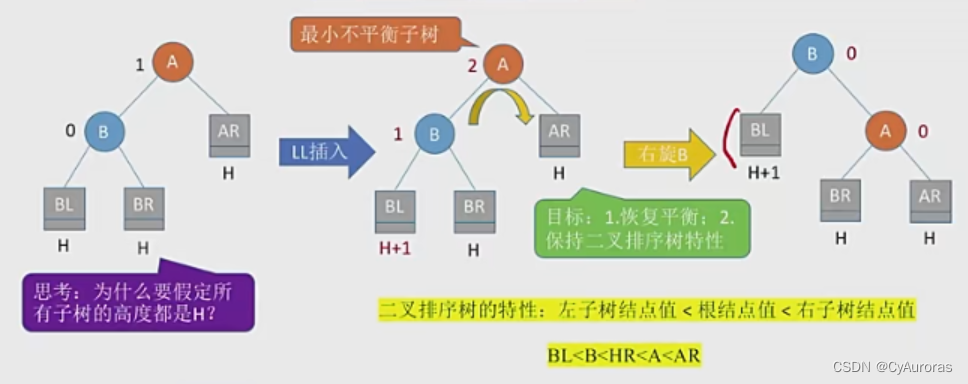
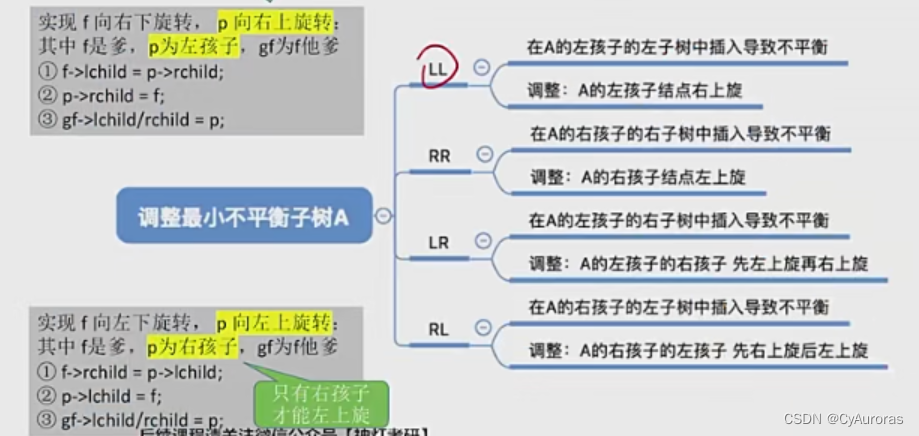
LL
右单旋转:A的左孩子B向右上旋转代替A位置,将A右旋转成B的右孩子,而B原本的右孩子成A的左孩子
RR
右单旋转:A的右孩子B向左上旋转代替A位置,将A左旋转成B的左孩子,而B原本的左孩子成A的右孩子

LR
先左后右双旋转:先将A结点孩子左孩子B的右孩子C向左上旋转提升到B的位置,然后在把C向右上旋转提升的A的位置

RL
先右后左双旋转:先将A结点孩子右孩子B的左孩子C向右上旋转提升到B的位置,然后在把C向左上旋转提升的A的位置
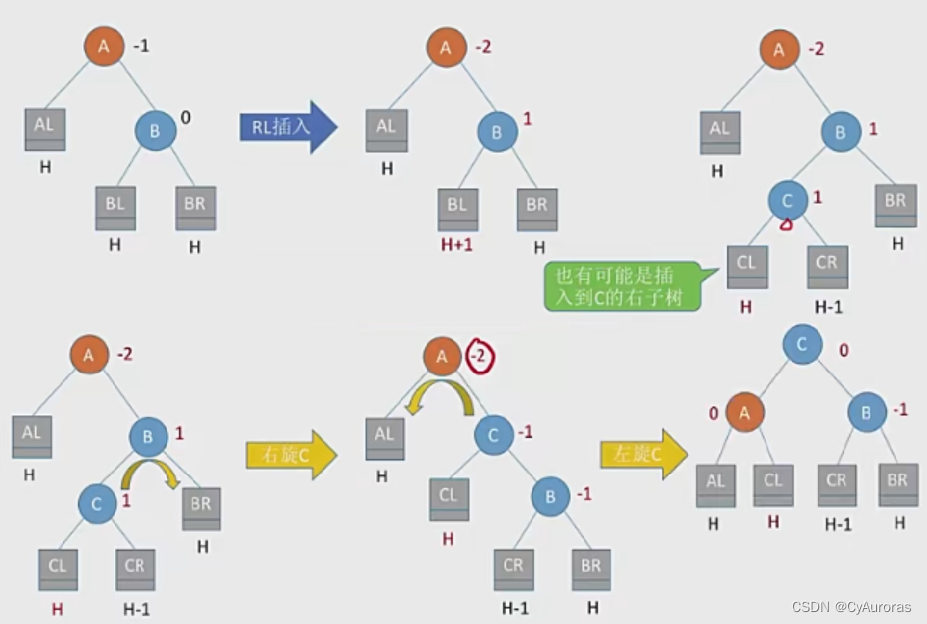
结
*查找效率分析
假设以表示深度为h的平衡树中含有的最少结点数
则,并且有
依此类推,
的高度
最大深度为,平衡二叉树的平均查找长度为
文献

删除
二叉排序数删除一样找值替代删除的,然后旋转解决不平衡
旋转LL,RR,LR,RL操作上面一样


三、红黑树
是二叉排序树--->左子树结点根结点
右子树结点
性质①:每个结点孩红色或黑色
②:根结点是黑色
③:叶结点(虚构的外部结点、NULL结点)都是黑色
④:不存在2个相邻的红结点
⑤:每个结点,从该结点到任意一叶结点的简单路径上,所包含黑结点相同
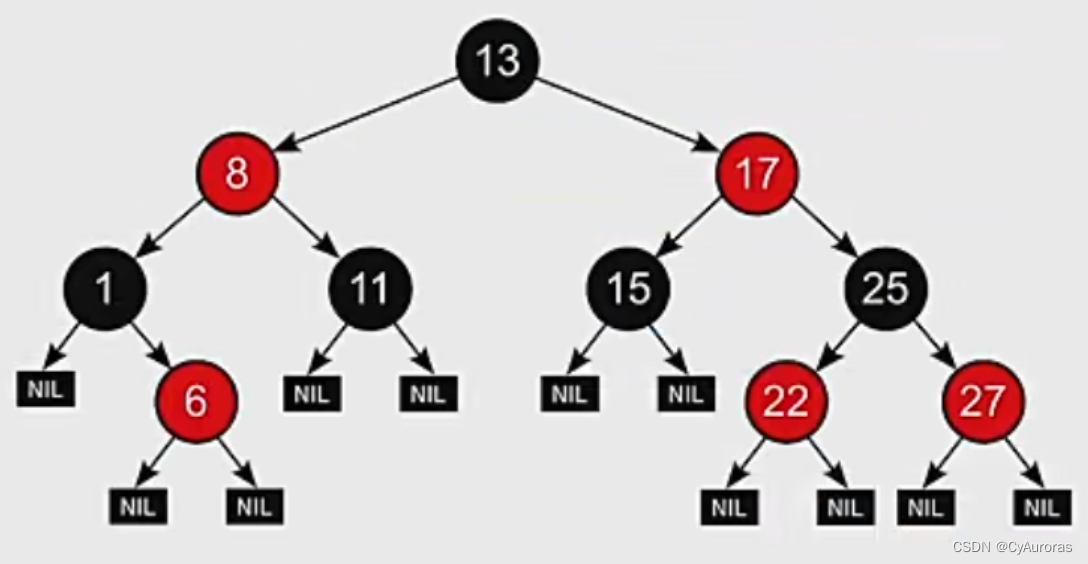
性质①:从根结点到叶结点的最长不大于最短路径的2倍
性质②:有n个内部结点的红黑树高度
*插入
左根右,根叶黑
不红红,黑路同


*删除
参考二叉排序树怎么删除的,然后破坏了红黑树性质,在根据插入那一套搞红黑树
四、B树

m叉树,任何结点至少个分叉。即至少含有
个关键字
m叉树平衡树,所有子树高度相同,就是B树

若含n个关键字的m阶B树,最小高度,最大高度多少
每个最多结点(m-1)个关键字,第一层1给结点,第二层m个节点,第三层个.....第n层
个
所以最小高度 ,因此
最大高度第一层1,第二层2,第三层 ...第h层
,第h+1层叶子节点,
个,所以n个关键字的B树比有n+1个叶节点,
即

*插入
中间往上提
*删除
非终端节点,直接前驱或者直接后继替换
终端节点:①兄弟够借(父拉下一个,兄弟上提一个)
②兄弟不够借(兄弟和上面一个合并)
五、B+树
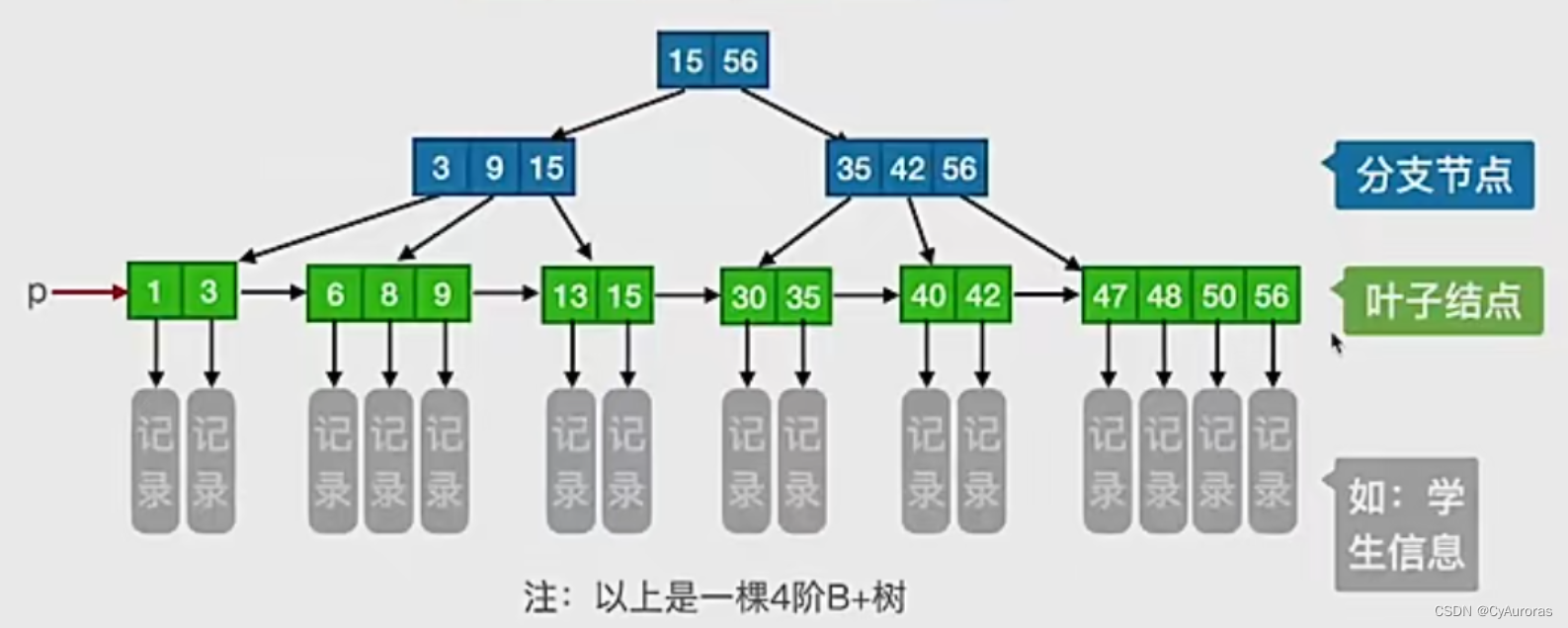
①:每个分支节点最多有m课子树
②:非叶根节点至多有两课子树,其他每个分支节点至少有课子树