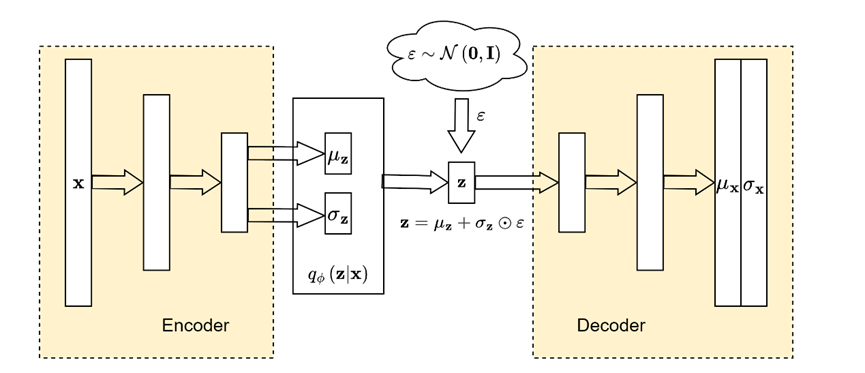
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 m x n 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 ‘B’ 移动到目标位置 ‘T’ :
玩家用字符 ‘S’ 表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。
地板用字符 ‘.’ 表示,意味着可以自由行走。
墙用字符 ‘#’ 表示,意味着障碍物,不能通行。
箱子仅有一个,用字符 ‘B’ 表示。相应地,网格上有一个目标位置 ‘T’。
玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
玩家无法越过箱子。
返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
示例 1:
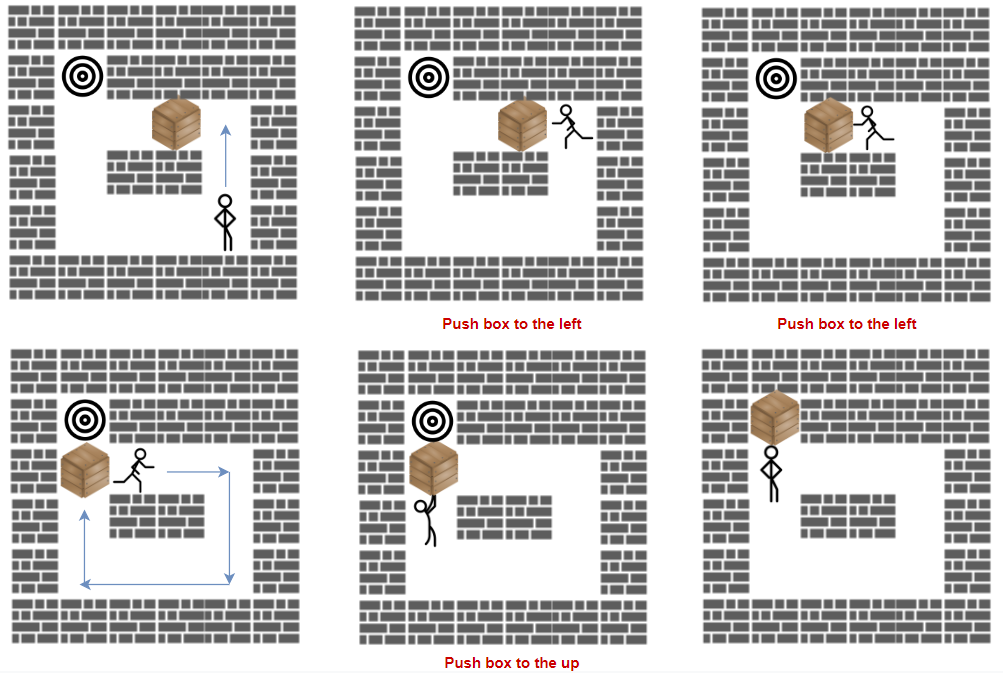
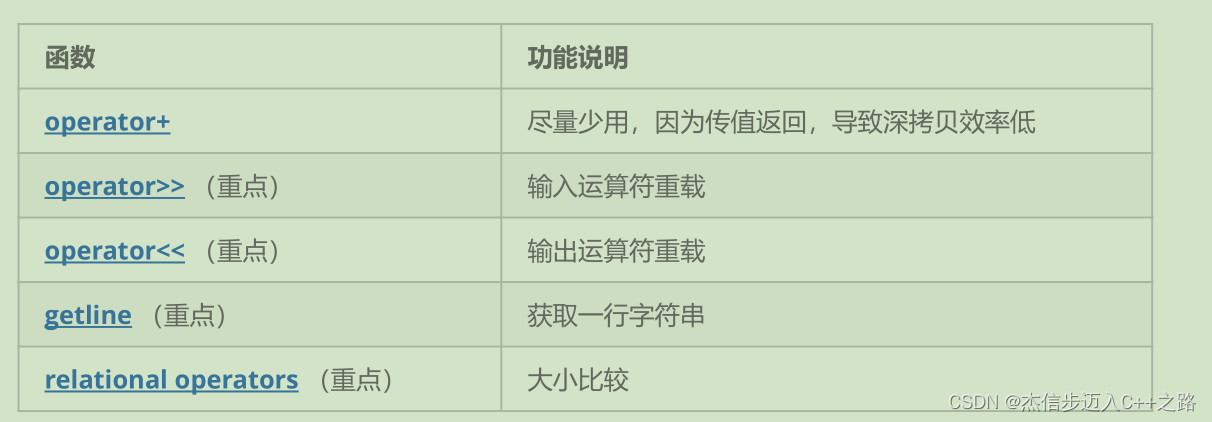
输入:grid = [[“#”,“#”,“#”,“#”,“#”,“#”],
[“#”,“T”,“#”,“#”,“#”,“#”],
[“#”,“.”,“.”,“B”,“.”,“#”],
[“#”,“.”,“#”,“#”,“.”,“#”],
[“#”,“.”,“.”,“.”,“S”,“#”],
[“#”,“#”,“#”,“#”,“#”,“#”]]
输出:3
解释:我们只需要返回推箱子的次数。
示例 2:
输入:grid = [[“#”,“#”,“#”,“#”,“#”,“#”],
[“#”,“T”,“#”,“#”,“#”,“#”],
[“#”,“.”,“.”,“B”,“.”,“#”],
[“#”,“#”,“#”,“#”,“.”,“#”],
[“#”,“.”,“.”,“.”,“S”,“#”],
[“#”,“#”,“#”,“#”,“#”,“#”]]
输出:-1
示例 3:
输入:grid = [[“#”,“#”,“#”,“#”,“#”,“#”],
[“#”,“T”,“.”,“.”,“#”,“#”],
[“#”,“.”,“#”,“B”,“.”,“#”],
[“#”,“.”,“.”,“.”,“.”,“#”],
[“#”,“.”,“.”,“.”,“S”,“#”],
[“#”,“#”,“#”,“#”,“#”,“#”]]
输出:5
解释:向下、向左、向左、向上再向上。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 20
grid 仅包含字符 ‘.’, ‘#’, ‘S’ , ‘T’, 以及 ‘B’。
grid 中 ‘S’, ‘B’ 和 ‘T’ 各只能出现一个。
这道题和上周华为暑期实习笔试的第三题有点相似,但个人感觉这道题难度更大。首先给这道题扣个帽子,属于一道搜索,但是不同于一般的搜索,这道题的搜索过程明显要麻烦一些。先说一下自己之前的错误思路:
①将整个问题分解为两个问题:人如何到达箱子边下以及箱子如何再到达终点。
②以人为起点进行广搜,当和箱子相遇之后就合为一体。
对于第一个思路,错误之处在于这是一个整体考虑的问题,并不是单独拆分就可以实现的,整体的最优值并不一定完全等于拆分后的最优值。而对于第二个思路,完全是读错了题目,题目要求的是,要计算推动箱子的次数,人推一下箱子之后,完全可以离开箱子跑到另一个位置来推。
最近一直在干组里的活,没时间仔细研究这道题,所以参考题解写了一版自己的代码。根据官方给的题解,这道题可以看作是一个复杂状态下的广搜,为什么说复杂呢,一般的广搜我们只需要考虑行动者的状态,一般就是那个能移动的个体,但是这道题,我们还需要将状态扩展为人和箱子的状态,箱子在不同的位置时,人即使坐标一样,也代表不同的状态。我们依然是以人为行动者,向四个方向进行搜索,当人的位置与当前箱子的位置重合,说明人推到了箱子,此时按照人移动的方向对箱子进行同样的移动,同时对状态数组进行增加来表示推过了一次箱子。此外,与一般的广度优先搜索不同,我们不能使用flag来标记哪些地方走过了哪些没走过,因为推动箱子之后可能存在更换方向推动箱子的情况,根据题解的方法,当我们推动箱子时,状态的改变会存入另一个队列,在下一轮循环中再进行广搜。
int dir[4][2] = {0, 1, 0, -1, 1, 0, -1, 0};
int step[25][25][25][25];
int height, length;
int minPushBox(vector<vector<char> >& grid) {
int sx, sy, ex, ey, bx, by;
height = grid.size();
length = grid[0].size();
for(int i=0; i<height; i++){
for(int j=0; j<length; j++){
for(int m=0; m<height; m++){
for(int n=0; n<length; n++){
step[i][j][m][n] = INT_MAX;
}
}
}
}
for(int i=0; i<height; i++){
for(int j=0; j<length; j++){
char c = grid[i][j];
if(c=='S'){
sx = i;
sy = j;
}
if(c=='T'){
ex = i;
ey = j;
}
if(c=='B'){
bx = i;
by = j;
}
}
}
step[sx][sy][bx][by] = 0;
queue<pair<pair<int, int>, pair<int, int> > > q;
q.push(make_pair(make_pair(sx, sy), make_pair(bx, by)));
while(!q.empty()){
queue<pair<pair<int, int>, pair<int, int> > > q1;
while(!q.empty()){
pair<pair<int, int>, pair<int, int> > temp = q.front();
q.pop();
int npx = temp.first.first;
int npy = temp.first.second;
int nbx = temp.second.first;
int nby = temp.second.second;
if(nbx==ex && nby==ey)
return step[npx][npy][nbx][nby];
for(int i=0; i<4; i++){
int tpx = npx + dir[i][0];
int tpy = npy + dir[i][1];
if(tpx<0||tpy<0||tpx>=height||tpy>=length||grid[tpx][tpy]=='#')
continue;
if(tpx==nbx && tpy==nby){
// 推到了箱子
int tbx = nbx + dir[i][0];
int tby = nby + dir[i][1];
if(tbx<0||tby<0||tbx>=height||tby>=length||grid[tbx][tby]=='#')
continue;
if(step[tpx][tpy][tbx][tpy] <= step[npx][npy][nbx][nby] + 1)
continue;
step[tpx][tpy][tbx][tby] = step[npx][npy][nbx][nby] + 1;
q1.push(make_pair(make_pair(tpx, tpy), make_pair(tbx, tby)));
}else{
// 没有推到箱子
if(step[tpx][tpy][nbx][nby] <= step[npx][npy][nbx][nby])
continue;
step[tpx][tpy][nbx][nby] = step[npx][npy][nbx][nby];
q.push(make_pair(make_pair(tpx, tpy), make_pair(nbx, nby)));
}
}
}
q.swap(q1);
}
return -1;
}
相比于题解的代码,我稍微改了一下数据结构的写法,按道理理解起来要稍微容易那么一点点,但是内存开销增加了不少,题解用的是一个数来表示二维的坐标,在定位以及四方向移动时会稍微麻烦点,所以我直接换成了四维数组,前两维表示人的位置,后两维表示箱子的位置,思路还是按照题解的思路。从人的位置开始四方向搜索,位置合法的情况下,判断是否与箱子的坐标产生了重叠,如果没有,那就继续搜索,但是在继续搜索的时候,为了避免重复走的问题,我们需要用step进行去重,也就是step[tpx][tpy][nbx][nby] <= step[npx][npy][nbx][nby]这个条件,这个条件实际上是在说,我们按照某个路径一直搜,搜索到头发现是个死路,如果不加这个条件,我们就会按照原路返回从而死循环,由于一开始我们设定了step的值全是最大值,只把起始位置改成了0,也就是说在第一轮搜索的过程中,所有走过的位置都改成了0,此时当走到死路的时候,就可以利用这个条件避免重走回头路。但是如果这个过程我们推到了箱子,事情就是另一回事了,我们推到了箱子,再走回头路就是允许的,因为此时我们可能是在利用回头路移动到箱子的另一个方向,但是回头路的回头路依然是不允许的,回头路的回头路依然是用step[tpx][tpy][nbx][nby] <= step[npx][npy][nbx][nby]进行筛选。值得一提的是,我们推到箱子之后,用q1进行了单独存储,这本质上是想让推到箱子作为开启下一次循环。我们每次循环,是从上一次的状态,在不走重复路的基础上,遍历所有路径找到能够推到箱子的新状态,下次在这部分的状态上进行继续的搜索。