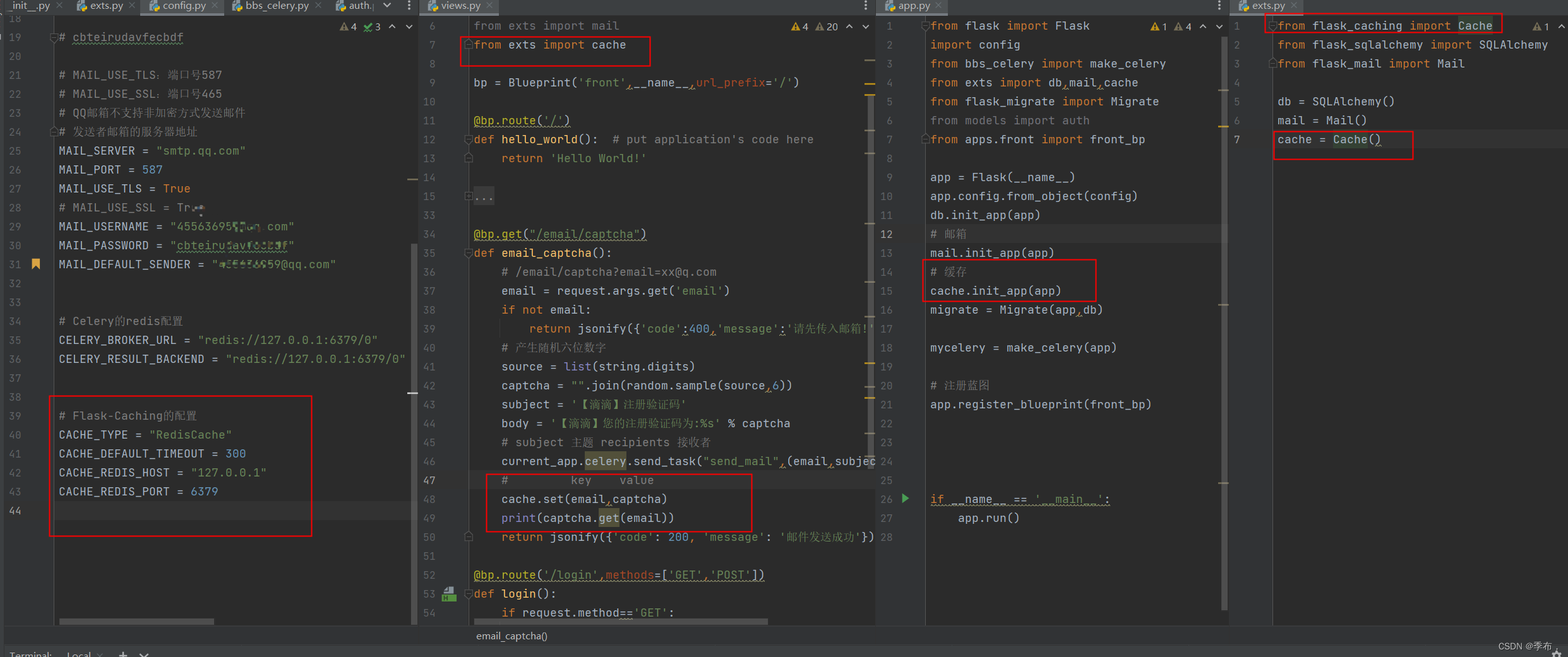
【数学】通俗理解泰勒公式(牛顿迭代法有用到)
文章目录
- 【数学】通俗理解泰勒公式(牛顿迭代法有用到)
- 1. 介绍
- 2. 通俗理解
- 2.1 近似计算
- 3. 泰勒公式的推导
- 4. 泰勒公式的定义
- 5. 扩展 — 麦克劳林公式
- 参考
1. 介绍
最近在看一些机器学习优化相关的方法(梯度下降、牛顿迭代等),里面又涉及到泰勒公式展开等,大学学的奈何都忘的差不多了,于是就看了一些博客,整理一下。
泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值。
- 所以泰勒公式是做什么用的?
- 简单来讲就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像),注意,逼近的时候一定是从函数图像上的某个点展开。
- 如果一个非常复杂函数,想求其某个值,直接求无法实现,这时候可以使用泰勒公式去近似的求该值,这是泰勒公式的应用之一。
- 泰勒公式在机器学习中主要应用于梯度迭代(牛顿迭代法)。
2. 通俗理解
下式是最简单的一类初等函数,也就是多项式。

- 多项式本身的运算仅是有限项加减法和乘法,所以在数值计算方面,多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。
2.1 近似计算
初等数学已经了解到一些函数如:

但是初等数学不曾回答怎样来计算它们,以
f
(
x
)
=
cos
x
f(x) = \small \cos x
f(x)=cosx 的近似计算为例,这里进行计算:
1)一次(线性)逼近
利用微分近似计算公式
f
(
x
)
≈
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
f(x) \small \approx f(\small x_{0}) + {f}'(\small x_{0})(x - \small x_{0})
f(x)≈f(x0)+f′(x0)(x−x0) (该式由导数/微分的极限表达公式转换得到),对
x
0
=
0
\small x_{0} = 0
x0=0 附近的
f
(
x
)
f(x)
f(x) 的线性逼近为:
f
(
x
)
≈
f
(
0
)
+
f
′
(
0
)
x
f(x) \small \approx f(0) + {f}'(0) x
f(x)≈f(0)+f′(0)x , 所以
f
(
x
)
=
cos
x
≈
1
f(x) = \small \cos x \small \approx 1
f(x)=cosx≈1,所以
f
(
x
)
f(x)
f(x) 在
x
0
=
0
\small x_{0} = 0
x0=0 附近的线性逼近函数
P
1
(
x
)
=
1
P_{1}(x) = 1
P1(x)=1,如下图:

- 线性逼近-优点:形式简单,计算方便;
- 线性逼近-缺点:离原点O越远,近似度越差。
2)二次逼近
使用二次多项式 p 2 ( x ) = a 0 + a 1 x + a 2 x 2 p_2(x) = a_0 + a_1x + a_2 x^2 p2(x)=a0+a1x+a2x2 来逼近 f ( x ) = cos x f(x) = \small \cos x f(x)=cosx,我们期望:

所以
cos
x
≈
P
2
(
x
)
=
1
−
x
2
2
\small \cos x \small \approx \small P_{2}\left ( x \right ) = 1 - \small \frac{x^{2}}{2}
cosx≈P2(x)=1−2x2,如下图:

- 二次逼近要比线性逼近好得多,但局限于 [ − π 2 , π 2 ] [ \small -\frac{\pi }{2},\small \frac{\pi }{2} ] [−2π,2π] 内,在这个范围之外,图像明显差异很大。
- 为什么我们期望两个函数在某一点的函数值 、一阶导数值、二阶导数值相等?
- 因为这些值表达了函数(图像)最基本和最主要的性质,这些性质逼近即可以使得两个函数逼近(由上面函数图像可以直观地看出来)。这也是泰勒公式的基本思想。
3)八次逼近
使用八次多项式
p
8
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
8
x
8
p_8(x) = a_0 + a_1x + a_2 x^2 + ... + a_8 x^8
p8(x)=a0+a1x+a2x2+...+a8x8 来逼近
f
(
x
)
=
cos
x
f(x) = \small \cos x
f(x)=cosx,我们期望:

因此,可以得到:

-
图像如下图:

-
P 8 ( x ) \small P_{8}\left ( x \right ) P8(x) (绿色图像) 比 P 2 ( x ) \small P_{2}\left ( x \right ) P2(x) (蓝色图像) 更大范围内更接近余弦函数 (红色图像)
综上,由上述3次不同程度的函数逼近可以看出:对于精确度要求较高且需要估计误差的时候,必须用高次多项式来近似表达函数,同时给出误差公式 。以上就是利用多项式函数去逼近给定函数的一个过程。
3. 泰勒公式的推导
由此引出一个问题:给定一个函数
f
(
x
)
\small f\left ( x \right )
f(x),要找一个在指定点
x
0
\small x_{0}
x0 附近与
f
(
x
)
\small f\left ( x \right )
f(x) 很近似的多项式函数
P
(
x
)
\small P\left ( x \right )
P(x),记为:

使得
f
(
x
)
≈
P
n
(
x
)
\small f\left ( x \right ) \small \approx \small P_{n}\left ( x \right )
f(x)≈Pn(x) 并且使得两者误差
R
n
(
x
)
=
f
(
x
)
−
P
n
(
x
)
\small R_{n}\left ( x \right ) = f\left ( x \right ) - P_{n}\left ( x \right )
Rn(x)=f(x)−Pn(x) 可估计。所以要找的多项式应该满足什么条件,误差是什么?
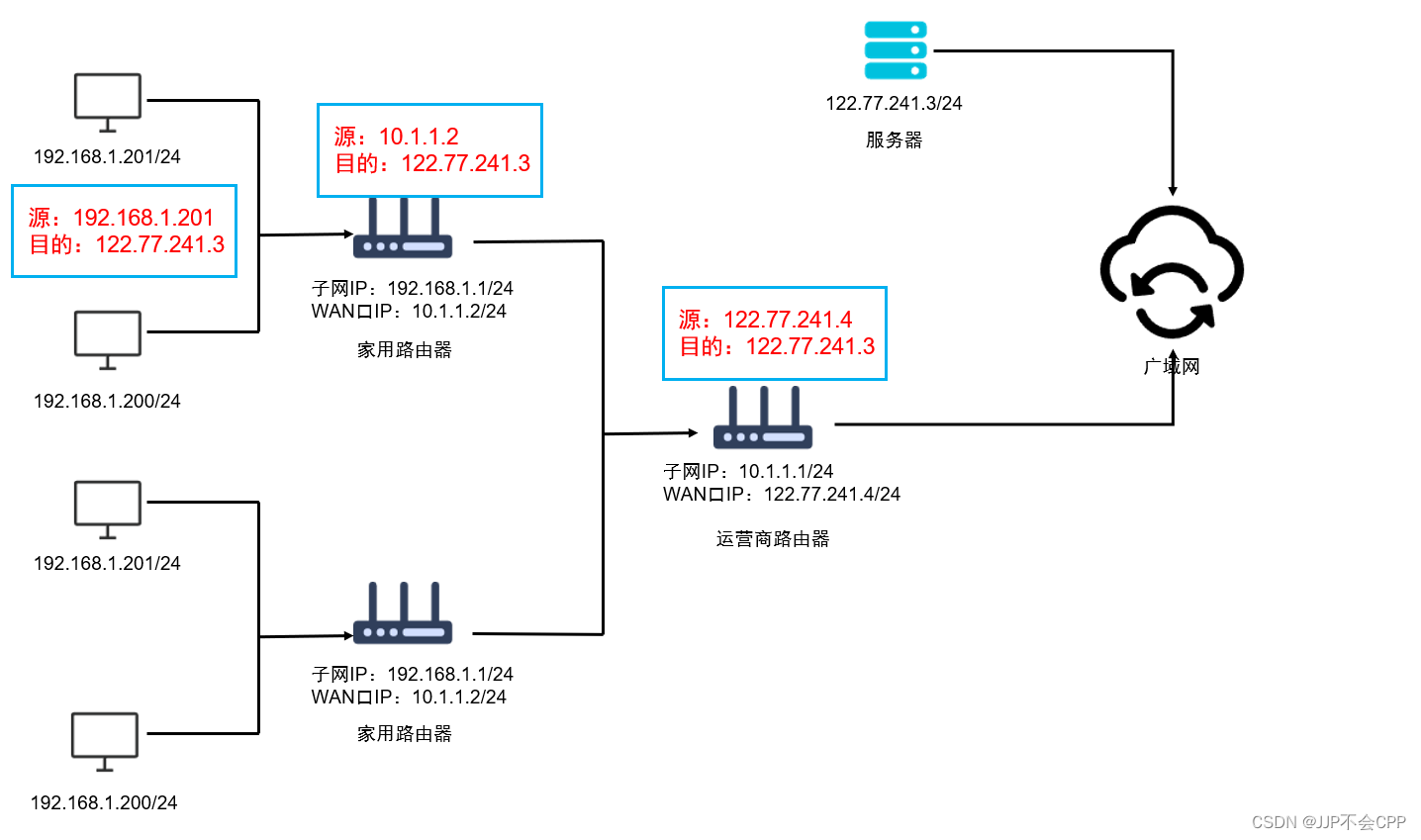
- 从几何上看, y = f ( x ) \small y = f\left ( x \right ) y=f(x), y = P n ( x ) \small y = P_{n}\left ( x \right ) y=Pn(x) 代表两条曲线,如下图:

使它们在
x
0
\small x_{0}
x0 的附近很靠近,很明显:
-
首先要求两曲线在 ( x 0 , f ( x 0 ) ) \small \left ( x_{0},f\left ( x_{0} \right ) \right ) (x0,f(x0)) 点相交,即 P n ( x 0 ) = f ( x 0 ) \small P_{n}\left ( x_{0} \right ) = f\left ( x_{0} \right ) Pn(x0)=f(x0)
-
如果要靠得更近,还要求两曲线在 ( x 0 , f ( x 0 ) ) \small \left ( x_{0},f\left ( x_{0} \right ) \right ) (x0,f(x0)) 点相切,(由图像可以直观看出,相交 [ 棕色和红色图像 ] 和 相切 [ 绿色和红色图像 ],两曲线在 x 0 \small x_{0} x0 附近的靠近情况明显差异很大,相切更接近),即 P n ′ ( x 0 ) = f ′ ( x 0 ) \small {P_{n}}'\left ( x_{0} \right ) = {f}'\left ( x_{0} \right ) Pn′(x0)=f′(x0)
-
如果还要靠得更近,还要求曲线在 ( x 0 , f ( x 0 ) ) \small \left ( x_{0},f\left ( x_{0} \right ) \right ) (x0,f(x0)) 点弯曲方向相同,(如上图,弯曲方向相反 [ 绿色和红色图像 ];弯曲方向相同[ 蓝色和红色图像 ],明显在离 x 0 \small x_{0} x0 很远的地方,弯曲方向相同两函数的差异更小一点),即 P n ′ ′ ( x 0 ) = f ′ ′ ( x 0 ) \small {P_{n}}''\left ( x_{0} \right ) = {f}''\left ( x_{0} \right ) Pn′′(x0)=f′′(x0) ,进而可推想:若在 ( x 0 , f ( x 0 ) ) \small \left ( x_{0},f\left ( x_{0} \right ) \right ) (x0,f(x0)) 附近有 P n ′ ( x 0 ) = f ′ ( x 0 ) \small {P_{n}}'\left ( x_{0} \right ) = {f}'\left ( x_{0} \right ) Pn′(x0)=f′(x0), P n ′ ′ ( x 0 ) = f ′ ′ ( x 0 ) ⋯ ⋯ ⋯ P n ( n ) ( x 0 ) = f n ( x 0 ) \small {P_{n}}''\left ( x_{0} \right ) = {f}''\left ( x_{0} \right ) \small \cdots \cdots \cdots \small P_{n}^{\left ( n \right )}\left ( x_{0} \right ) = f^{n}\left ( x_{0} \right ) Pn′′(x0)=f′′(x0)⋯⋯⋯Pn(n)(x0)=fn(x0),近似程度越来越好。
综上所述,所要找的多项式应满足下列条件:

- 解释一下上面的转换时如何做的,以上面第三行的二阶导数为例:
- 第一个箭头的转换:将 P n ( x ) \small P_{n}\left ( x \right ) Pn(x) 求二阶导函数后将 x 0 \small x_{0} x0 带入,求得 P n ′ ′ ( x 0 ) = 2 ! a 2 \small {P_{n}}''\left ( x_{0} \right ) = 2!a_{2} Pn′′(x0)=2!a2
- 第二个箭头的转换:所以 f ′ ′ ( x 0 ) = 2 ! a 2 \small {f}''\left ( x_{0} \right ) = 2!a_{2} f′′(x0)=2!a2,所以 a 2 = 1 2 ! f ′ ′ ( x 0 ) \small a_{2} = \frac{1}{2!}{f}''\left ( x_{0} \right ) a2=2!1f′′(x0)
多项式函数
p
n
(
x
)
=
a
0
+
a
1
(
x
−
x
0
)
+
a
2
(
x
−
x
0
)
2
+
.
.
.
+
a
n
(
x
−
x
0
)
n
p_n(x) = a_0 + a_1(x - x0) + a_2 (x - x0)^2 + ... + a_n (x - x0)^n
pn(x)=a0+a1(x−x0)+a2(x−x0)2+...+an(x−x0)n 中的系数
a
\small a
a 可以全部由
f
(
x
)
\small f\left ( x \right )
f(x) 表示,则得到:

其中误差为
R
n
(
x
)
=
f
(
x
)
−
P
n
(
x
)
\small R_{n} \left ( x \right ) = f\left (x \right ) - P_{n}\left ( x \right )
Rn(x)=f(x)−Pn(x)。 因为是用多项式函数去无限逼近给定的函数,所以两者之间肯定存在一丢丢的误差。
4. 泰勒公式的定义
所以我们就得到了泰勒公式的定义:
如果函数
f
(
x
)
\small f\left ( x \right )
f(x) 在含
x
0
\small x_{0}
x0 的某个开区间
(
a
,
b
)
\small \left ( a,b \right )
(a,b) 内具有直到
(
n
+
1
)
\small \left ( n+1 \right )
(n+1) 阶导数,则对
∀
x
∈
(
a
,
b
)
\small \forall x \in \left ( a,b \right )
∀x∈(a,b),有:

其中余项 (即误差)
R
n
(
x
)
=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
x
0
)
n
+
1
\small R_{n}\left ( x \right ) = \frac{f^{\left ( n+1 \right )}(\xi )}{\left ( n+1 \right )!}(x-x_{0})^{n+1}
Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1,
ξ
\xi
ξ 在
x
0
\small x_{0}
x0 与
x
x
x 之间。 泰勒公式的余项表达方式有好几种,前面这表示方法称为 n 阶泰勒展开式的拉格朗日余项。
- 拉格朗日余项即是n阶泰勒公式又多展开了一阶,n 变为 n+1。
- 注意,这里的余项即为误差,因为使用多项式函数在某点展开,逼近给定函数,最后肯定会有一丢丢的误差,我们称之为余项。
5. 扩展 — 麦克劳林公式
麦克劳林公式是泰勒公式的一种特殊情况:即当
x
0
=
0
\small x_{0} = 0
x0=0 时的泰勒公式。所以将
x
0
=
0
\small x_{0} = 0
x0=0 代入公式,即得:

几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:

佩亚诺余项为
(
x
−
x
0
)
n
\small \left ( x-x_{0} \right )^{n}
(x−x0)n 的高阶无穷小:

参考
【1】https://blog.csdn.net/xiaojinger_123/article/details/127442655




![[googletest] --- 简易使用教程](https://img-blog.csdnimg.cn/8e9823aab4a5441bb433d745a7bd8df5.jpeg)