---

前言

二分查找常见的是在一维数据中进行，在我的上一篇文章中已经有介绍。

一维数组查找：BM18 二维数组中的查找

本文介绍的是在二维数组中查找某个数字，有些解法可以参考在一维数组中二分查找，有些解法则是全新的思路

常见题目为：
在一个二维数组array中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7，返回 true。

给定 target = 3，返回 false。

---

一、解法1：逐行使用二分搜索

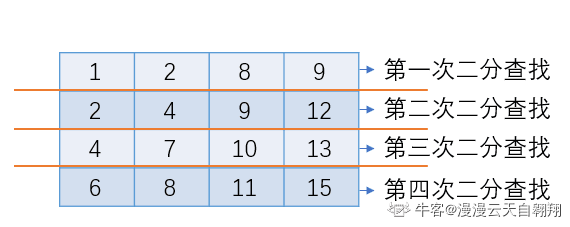
解题思路： 利用数组每行每列都是递增特性。

这种思路比较简单易懂，从第一行开始，每行依次进行二分搜索，找到答案就返回 true，每一行都找不到就返回 false 。

public class Solution {
    public boolean Find(int target, int [][] array) {
        int i,j=0;
        for(i = 0; i < array.length ;i++){
            if(binary_search(target,array[i])) return true;
        }
        return false;
    }
    
    public boolean binary_search(int target,int[] arr){
        int left = 0;
        int right = arr.length - 1;
        while(left <= right){
            int mid = (right - left)/2 +left ;
            if(arr[mid] > target){
                right = mid - 1;
            }else if(arr[mid] < target){
                left = mid + 1;
            }else{
                return true;
            }
        }
        return false;
    }
}

时间复杂度：

二、解法2：线性搜索（推荐）

解题思路： 利用二维数组行列递增特性

由于行列递增，可以得出：

a.在一列中的某个数字，其上的数字都比它小

b.在一行中的某个数字，其右的数字都比它大

搜索流程：

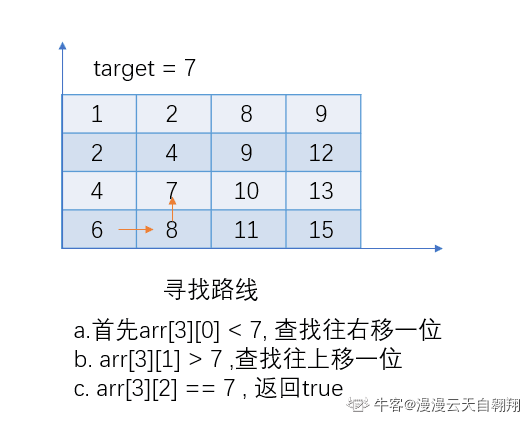
a.首先从数组左下角搜索.

b.如果当前数字大于target,那么查找往上移一位,如果当前数字小于target,那么查找往右移一位。

c.查找到target,返回true; 如果越界，返回false;

public class Solution {
    public boolean Find(int target, int [][] array) {
        if(array.length == 0){
            return false;
        }
        int l = array.length; //行数
        int r = array[0].length;//列数
        int i = l - 1;//定位所在行
        int j = 0;//定位所在列
        while(j < r && i>= 0){//要保证array[i][j]在数组中，不出现索引越界
            if(array[i][j] == target) return true;
            else if(array[i][j] > target) i--;
            else j++;
        }
        return false;
    }
}

时间复杂度：

---