本篇介绍第二个机器学习算法：决策树算法，我们经常使用决策树处理分类问题，近来的调查表明决策树也是最经常使用的数据挖掘算法。

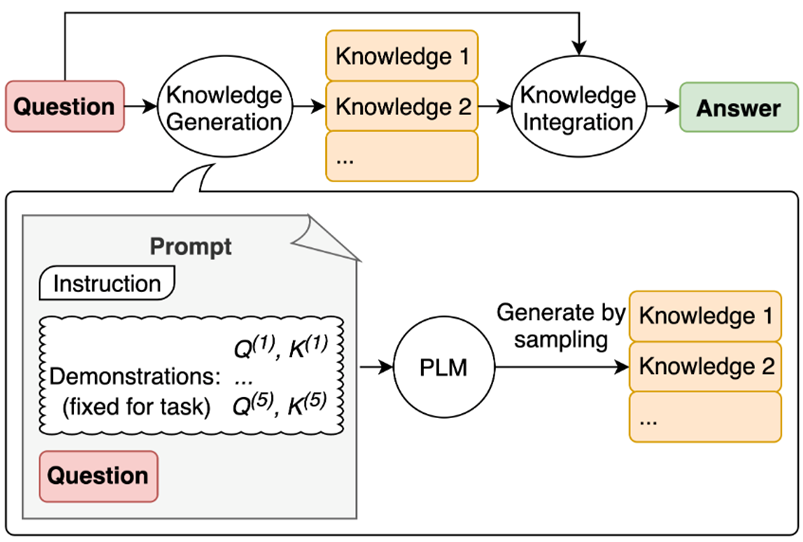
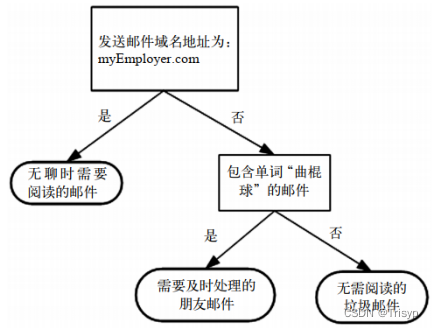
图1所示的流程图就是一个决策树，长方形代表判断模块（decision block），椭圆形代表终止模块（terminating block），表示已经得出结论，可以终止运行。从判断模块引出的左右箭头称作分支（branch），它可以到达另一个判断模块或者终止模块。

它构造了一个假想的邮件分类系统，首先检测发送邮件域名地址。如果地址为myEmployer.com，则将其放在分类“无聊时需要阅读的邮件”中。如果邮件不是来自这个域名，则检查邮件内容里是否包含单词曲棍球，如果包含则将邮件归类到“需要及时处理的朋友邮件”，如果不包含则将邮件归类到“无需阅读的垃圾邮件”。

概念：是一种基本的分类与回归方法，决策树模型呈树形结构，可以认为是if-then的集合（互斥并且完备：即每一个实例都被一条路径或一条规则所覆盖，而且，只被一条路径或一条规则所覆盖。）或者定义在特征空间与类空间上的条件概率分布。

定义：分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点有两种类型：内部结点（internal node）和叶结点（leaf node）。内部结点表示一个特征或属性，叶结点表示一个类。

优点：计算复杂度不高，输出结果易于理解和解释（具有可读性），对中间值的缺失不敏感，可以处理不相关特征数据，分类速度快。

缺点：可能会产生过度匹配问题；

适用数据范围：数值型和标称型

该伪代码是一个递归函数。

每次划分数据集时我们只选取一个特征属性，如果训练集中存在20个特征，第一次我们选择哪个特征作为划分的参考属性呢？在回答这个问题之前，我们必须采用量化的方法判断如何划分数据。

熵：熵定义为信息的期望值，集合信息的度量方式称为香农熵或者简称为熵。如果待分类的事务可能划分在多个分类之中，则符号的信息定义为，其中是选择该分类的概率。为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值，通过下面的公式得到：，其中n是分类的数目。可验证。

 条件熵：随机变量X在给定的条件下随机变量Y的条件熵：

信息增益：表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。即在划分数据集之前之后信息发生的变化称为信息增益。获得信息增益最高的特征就是最好的选择。特征A对训练数据集D的信息增益（也叫互信息）。不同的特征往往具有不同的信息增益。信息增益大的特征具有更强的分类能力。计算流程如下：

划分数据集：我们将对每个特征划分数据集的结果计算一次信息熵，然后判断按照哪个特征划分数据集是最好的划分方式。

递归构造决策树：通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。

算法流程：开始，构建根结点，将所有训练数据都放在根结点。选择一个最优特征，按照这一特征将训练数据集分割成子集，使得各个子集布一个在当前条件下最好的分类。如果这些子集已经能够被基本正确分类，那么构建叶结点，井将这些子集分到所对应的叶结点中去；如果还有子集不能被基本正确分类，那么就对这些子集选择新的最优特征，继续对其进行分剖，构建相应的结点。如此递归地进行下去，直至所有训练数据子集被基本正确分类，或者没有合适的特征为止。

一、ID3

ID3算法：从根结点（root node）开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点：再对子结点边归地调用以上方法，构建决策树：直到所有特征的信息增益均很小或没有特征可以选择为止。一般我们并不构造新的数据结构，而是使用Python语言内嵌的数据结构字典存储树节点信息。ID3相当于用极大似然法进行概率模型的选择。本篇使用ID3算法来划分数据集。算法流程如下：

工作原理：得到原始数据集，然后基于最好的属性值划分数据集，由于特征值可能多于两个，因此可能存在大于两个分支的数据集划分。第一次划分之后，数据将被向下传递到树分支的下一个节点，在这个节点上，我们可以再次划分数据。因此我们可以采用递归的原则处理数据集，递归结束的条件是：程序遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的分类。

二、C4.5

信息增益比：以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增益比（information gain ratio）可以对这一问题进行校正。特征A对训练数据集D的信息增益比：

C4.5算法：在生成的过程中，用信息增益比来选择特征。算法流程如下：

复杂的决策树可以非常好地匹配了实验数据，然而这些匹配选项可能太多了。我们将这种问题称之为过度匹配（overfitting）。为了减少过度匹配问题，我们可以裁剪决策树，去掉一些不必要的叶子节点。如果叶子节点只能增加少许信息，则可以删除该节点，将它并入到其他叶子节点中。剪枝：在决策树学习中将己生成的树进行简化的过程称为剪枝（pruning）。具体地，剪枝从己生成的树上裁掉一些子树或叶结点，并将其根结点或父结点作为新的叶结点，从而简化分类树模型。定义决策树学习的损失函数如下：

|T|是树T的叶节点个数，即模型复杂度，C(T)是树T对训练数据的预测误差，是控制二者的影响，较大的促使选择较简单的模型，较小的促使选择较复杂的模型。 

三、CART

CART算法：算法由两步完成：（1）决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大；（所以决策树是一种贪心算法，CART则使用二元切分法来处理连续型变量）（2）决策树剪枝：用验证数据集对己生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。CART剪枝算法由两部组成：｛首先从生成算法产生的决策树底端开始不断剪枝，直到的根结点，形成一个子树序列：，然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树。具体算法流程如下：

案例（预测隐形眼睛类型）：隐形眼镜数据集是非常著名的数据集，它包含很多患者眼部状况的观察条件以及医生推荐的隐形眼镜类型。隐形眼镜类型包括硬材质、软材质以及不适合佩戴隐形眼镜。数据来源于UCI数据库，本篇为了更简单展示对数据做了简单更改。

Python3实现完整代码：

import operator
from numpy import log2, nonzero, inf, shape, var, mean, mat


def calc_shannon_ent(data_set):
    # 计算香农熵
    num_entries = len(data_set)
    label_counts = {}
    for vec in data_set:
        current_label = vec[-1]
        if current_label not in label_counts.keys():
            label_counts[current_label] = 0
        label_counts[current_label] += 1
        shannon_ent = 0
        for key in label_counts:
            prob = label_counts[key] / num_entries
            shannon_ent -= prob * log2(prob)
        return shannon_ent


def split_data_set(data_set, axis, value):
    # 取出第axis个特征值为value的所有样本
    ret_data_set = []
    for vec in data_set:
        if vec[axis] == value:  # 拿出第axis个特征值为value的所有样本
            reduced_vec = vec[:axis]
            reduced_vec.extend(vec[axis + 1:])
            ret_data_set.append(reduced_vec)
    return ret_data_set


def choose_best_feature(data_set):
    # 选取特征，划分数据集，计算得出最好的划分数据集的特征
    num_features = len(data_set[0]) - 1
    base_entropy = calc_shannon_ent(data_set)  # 整个数据集的信息熵
    best_info_gain = 0.0
    best_feature = -1
    for i in range(num_features):  # 对于第i个特征，计算其信息熵
        feat_list = [d[i] for d in data_set]
        unique_vals = set(feat_list)  # 获取该特征可能存在的值
        new_entropy = 0.0
        for value in unique_vals:  # 对于每个特征值，计算其子集的信息熵
            sub_data_set = split_data_set(data_set, i, value)
            prob = len(sub_data_set) / len(data_set)
            new_entropy += prob * calc_shannon_ent(sub_data_set)
        info_gain = base_entropy - new_entropy  # 计算信息增益
        if info_gain > best_info_gain:
            best_info_gain = info_gain
            best_feature = i  # 获取信息增益最大的特征对应的索引
    return best_feature


def majority_cnt(class_list):
    # 投票表决
    class_count = {}
    for vote in class_list:
        if vote not in class_count.keys():
            class_count[vote] = 0
        class_count[vote] += 1
    sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)  # 按键值排序字典
    return sorted_class_count[0][0]  # 返回出现次数最多的分类名称


def create_tree(data_set, labels):
    # 递归构造决策树
    class_list = [d[-1] for d in data_set]
    if len(data_set[0]) == 1:  # 如果只有一个特征标签，则用投票法
        return majority_cnt(class_list)
    if class_list.count(class_list[0]) == len(class_list):  # 如果特征下所有值完全相同则停止继续划分
        return class_list[0]
    best_feat = choose_best_feature(data_set)  # 最好划分的特征索引
    best_feat_label = labels[best_feat]
    my_tree = {best_feat_label: {}}  # 决策树
    del labels[best_feat]
    feat_values = [d[best_feat] for d in data_set]
    unique_vals = set(feat_values)
    for value in unique_vals:
        sub_labels = labels[:]
        my_tree[best_feat_label][value] = create_tree(split_data_set(data_set, best_feat, value), sub_labels)
    return my_tree


def classify(input_tree, feat_labels, test_vec):
    # 预测分类
    if isinstance(input_tree, str):
        return input_tree
    first_str = list(input_tree.keys())[0]
    second_dict = input_tree[first_str]
    feat_index = feat_labels.index(first_str)
    for key in second_dict.keys():
        if test_vec[feat_index] == key:
            class_label = classify(second_dict[key], feat_labels, test_vec)
        else:
            class_label = second_dict[key]
    return class_label


# -------------------------------------------------------------------------------
# CART算法
class CART():
    def __init__(self, data_set):
        self.data_set = data_set

    def bin_split_dataSet(self, dataSet, feature, value):
        try:
            # tmp = dataSet[:, feature].tolist()
            # tmp2 = matrix([t[0] for t in tmp])
            tmp = dataSet[:, feature]
            mat0_index = nonzero(tmp > value)
            if len(mat0_index[0]) > 0:
                mat0 = dataSet[mat0_index[0], :][0]
            else:
                mat0 = []
            mat1_index = nonzero(tmp <= value)
            if len(mat1_index[0]) > 0:
                mat1 = dataSet[nonzero(dataSet[:, feature] <= value)[0], :][0]
            else:
                mat1 = []
            return mat0, mat1
        except Exception as e:
            print(repr(e))
            return [], []

    def regLeaf(self, dataSet):
        # 生成叶节点
        return mean(dataSet[:, -1])

    def regErr(self, dataSet):
        # 计算目标变量的平方误差
        return var(dataSet[:, -1]) * shape(dataSet)[0]

    def chooseBestSplit(self, dataSet, ops=(1, 4)):
        # leafType是对创建叶节点的函数的引用,errType是对总方差计算函数的引用
        # ops是一个用户定义的参数构成的元组，用以完成树的构建
        leafType = self.regLeaf
        errType = self.regErr
        tolS = ops[0]
        tolN = ops[1]
        # if all the target variables are the same value: quit and return value
        if set(dataSet[:, -1].T.tolist()[0]).__len__() == 1:  # exit cond 1
            return None, leafType(dataSet)
        m, n = shape(dataSet)
        # the choice of the best feature is driven by Reduction in RSS error from mean
        S = errType(dataSet)
        bestS = inf
        bestIndex = 0
        bestValue = 0
        for featIndex in range(n - 1):
            tmp = dataSet[:, featIndex].tolist()
            tmp2 = [t[0] for t in tmp]
            for splitVal in set(tmp2):
                mat0, mat1 = self.bin_split_dataSet(dataSet, featIndex, splitVal)
                if shape(mat0)[0] < tolN or shape(mat1)[0] < tolN:
                    continue
                newS = errType(mat0) + errType(mat1)
                if newS < bestS:
                    bestIndex = featIndex
                    bestValue = splitVal
                    bestS = newS
        # if the decrease (S-bestS) is less than a threshold don't do the split
        if (S - bestS) < tolS:
            return None, leafType(dataSet)  # exit cond 2
        mat0, mat1 = self.bin_split_dataSet(dataSet, bestIndex, bestValue)
        if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN):  # exit cond 3
            return None, leafType(dataSet)
        return bestIndex, bestValue  # returns the best feature to split on
        # and the value used for that split

    def creat_cart_tree(self, dataSet, ops=(1, 4)):
        feat, val = self.chooseBestSplit(dataSet, ops)
        if feat is None:
            return val
        ret_tree = {}
        ret_tree['spInd'] = feat
        ret_tree['spVal'] = feat
        lset, rset = self.bin_split_dataSet(dataSet, feat, val)
        ret_tree['left'] = self.creat_cart_tree(lset, ops)
        ret_tree['right'] = self.creat_cart_tree(rset, ops)
        return ret_tree


if __name__ == '__main__':
    data_set = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    ret_data_set0 = split_data_set(data_set, 0, 0)
    ret_data_set1 = split_data_set(data_set, 0, 1)
    shannon_ent = calc_shannon_ent(data_set)
    print("shannon entropy: ", shannon_ent)
    best_feature = choose_best_feature(data_set)
    print("best feature: ", best_feature)
    my_tree = create_tree(data_set, labels)
    print("my tree: ", my_tree)
    labels = ['no surfacing', 'flippers']
    class_label = classify(my_tree, labels, [1, 1])
    print("test vec:", [1, 1], "is belong: ", class_label)

    # 预测隐形眼镜类型
    import pandas as pd

    data = pd.read_table("lenses.txt", header=None)
    data.columns = ['age', 'prescript', 'astigmatic', 'tear_rate', "tag"]
    data_set = list(data.to_xarray().to_array().data)
    data_set1 = []
    for i in range(len(data_set[0])):
        data_set1.append([d[i] for d in data_set])
    labels = ['age', 'prescript', 'astigmatic', 'tear_rate']
    lenses_tree = create_tree(data_set1, labels)
    print("lenses tree: ", lenses_tree)

    # cart算法
    import pandas as pd

    data = pd.read_table("ex00.txt", header=None)
    data_set = list(data.to_xarray().to_array().data)
    data_set1 = []
    for i in range(len(data_set[0])):
        data_set1.append([d[i] for d in data_set])
    data_mat = mat(data_set1)
    cart = CART(data_mat)
    ret_tree = cart.creat_cart_tree(data_mat)

备注：

隐形眼镜数据集和ex00.txt直接去源码地址下载www.manning.com/MachineLearninginAction