一、实验目的及要求
一、实验的目的与要求:
1、掌握 MATLAB的一维数据插值法
2、通过比较不同次数的多项式拟合效果,了解多项式拟合的原理
3、掌握 MATLAB的多项式拟合的特点和方法
4、掌握 MATLAB的多项式表示与运算
二、实验原理
1、Matlab中,多项式的表示,多项式的四则运算;
2、MATLAB的polyval、poly2sym、root、poly、conv函数;
3、数据插值可以根据有限个点的取值状况,合理估算出附近其他点的取值。MATLAB的interp1函数,用于实现一维插值的,method用于指定插值方法,可取值如下:'nearest’是最邻近插值; 'linear’线性插值(默认值); 'spline’三次样条插值; 'cubic’立方插值。;
4、MATLAB的polyfit函数用于求最小二乘拟合多项式的系数;
二、实验设备及要求
PC机100台及MATLAB软件
三、实验内容与步骤
1)求一元高次多项式的根。
(2)求多项式 和 的乘积。
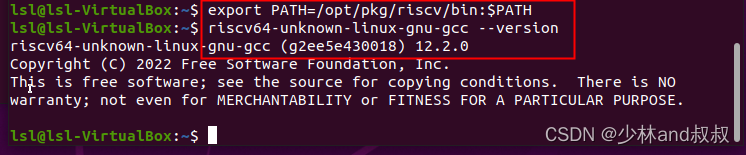
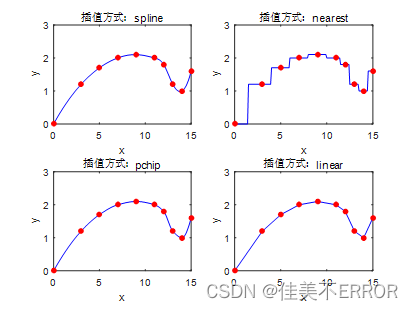
(3)在飞机制造中,机翼的加工是一项关键技术。由于机翼尺寸很大,通常在图纸中只能标出一些关键点的数据。下表给出了某型飞机机翼的下缘轮廓线数据,求每改变0.1时y的值。要求:插值方式分别用nearest、linear、spline、pchip四种,并在一个图像窗口中以子图形式绘制。
x 0 3 5 7 9 11 12 13 14 15
y 0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6
实验效果展示如下:
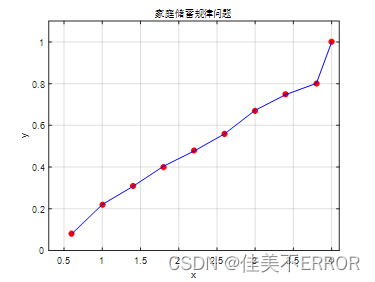
(4)以下是某市家庭收入x与家庭储蓄y之间的一组调查数据(单位:万元),请用数据拟合的方法试建立x与y的函数经验公式,要求:通过不断实验找一个函数,去逼近这些数据,并在屏幕输出该函数的符号形式。
x 0.6 1.0 1.4 1.8 2.2 2.6 3.0 3.4 3.8
y 0.08 0.22 0.31 0.4 0.48 0.56 0.67 0.75 0.8
拟合出来的曲线效果图如下所示
四、实验结果与数据处理
实验结果截图:
(1)

实验代码:coefficients = [1, -5, -30, 150, 0, 273, -1365, -820, 4100, 576, -2880];roots = roots(coefficients)
(2)

实验代码: f = [1, 3, 5, 7];
g = [8, -6, 0, -2];
product = conv(f, g)
(3)
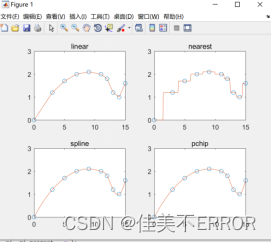
实验代码:% 存储机翼下缘轮廓线的数据
x = [0, 3, 5, 7, 9, 11, 12, 13, 14, 15];
y = [0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6];
% 生成插值点
xi = 0:0.1:15;
% 使用nearest插值方式
yi_nearest = interp1(x, y, xi, ‘nearest’);
% 使用linear插值方式
yi_linear = interp1(x, y, xi, ‘linear’);
% 使用spline插值方式
yi_spline = interp1(x, y, xi, ‘spline’);
% 使用pchip插值方式
yi_pchip = interp1(x, y, xi, ‘pchip’);
% 绘制图像
figure;
subplot(2, 2, 1);
plot(x, y, ‘o’, xi, yi_linear, ‘-’);
title(‘linear’);
subplot(2, 2, 2);
plot(x, y, ‘o’, xi, yi_nearest, ‘-’
title(‘nearest’);
subplot(2, 2, 3);
plot(x, y, ‘o’, xi, yi_spline, ‘-’);
title(‘spline’);
subplot(2, 2, 4);
plot(x, y, ‘o’, xi, yi_pchip, ‘-’);
title(‘pchip’);
(4)
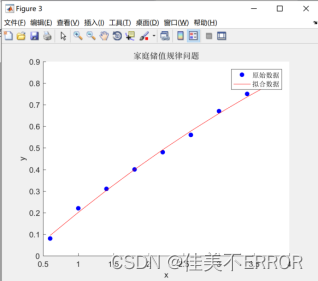
实验代码:x = [0.6, 1.0, 1.4, 1.8, 2.2, 2.6, 3.0, 3.4, 3.8];
y = [0.08, 0.22, 0.31, 0.4, 0.48, 0.56, 0.67, 0.75, 0.8];
coefficients = polyfit(x, y, 2);
y_fit = polyval(coefficients, x);
figure
scatter(x, y, ‘b’, ‘filled’)
hold on
plot(x, y_fit, ‘r’)
xlabel(‘x’)
ylabel(‘y’)
legend(‘原始数据’, ‘拟合数据’)
title(‘家庭储值规律问题’);
fprintf(‘拟合的多项式函数为: y = %.4fx^2 + %.4fx + %.4f\n’, coefficients(1), coefficients(2), coefficients(3));
五、实验分析与总结
实验越往后越难,但是实验四还是比较容易上手的,总体来说没有太多错误。每做完一个操作最后都要进行变量删除,方便进行下一个操作,不然可能得出错误答案。