一种可能的建模方法是基于列车的动力学方程和阻力方程,将列车视为单质点,忽略车厢间的车钩力和速度差。根据给定的参数,可以建立如下的方程:
$$m(p+1)\frac{dv}{dt}=F-f(v)-g(i)$$
$$f(v)=2.0895+0.0098v+0.006v^2$$
$$g(i)=mgi$$

其中,$m$是列车质量,$p$是旋转质量因子,$v$是列车速度,$t$是时间,$F$是列车牵引力或制动力,$f(v)$是列车所受基本阻力,$g(i)$是列车所受坡道附加阻力,$i$是坡度千分数。
为了求解这个微分方程,可以使用数值方法,如欧拉法或龙格-库塔法。具体的步骤如下:
1. 将时间区间$[0,T]$划分为$n$个小区间,每个区间的长度为$\Delta t=T/n$。令$t_k=k\Delta t,k=0,1,\dots,n$。
2. 给定初始条件$v_0=v(0)$和初始牵引力或制动力$F_0=F(0)$。
3. 对于$k=0,1,\dots,n-1$,根据数值方法计算$v_{k+1}=v(t_{k+1})$和$F_{k+1}=F(t_{k+1})$。例如,如果使用欧拉法,则有: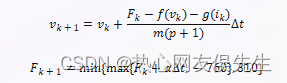
$$v_{k+1}=v_k+\frac{F_k-f(v_k)-g(i_k)}{m(p+1)}\Delta t$$
$$F_{k+1}=\min\{\max\{F_k+\alpha\Delta t,-760\},310\}$$
其中,$\alpha$是牵引力或制动力的变化率,可以根据不同的运行策略设定。注意,牵引力或制动力需要满足最大值和最小值的限制。
4. 根据$v_k$和$\Delta t$计算列车运行距离$s_k=s(t_k)$。例如,如果使用梯形法,则有:
$$s_{k+1}=s_k+\frac{v_k+v_{k+1}}{2}\Delta t$$
![]()
5. 根据$v_k,s_k,t_k,F_k$绘制所需的曲线。例如,速度-距离曲线就是$v=f(s)$,牵引制动力-距离曲线就是$F=f(s)$等。
6. 为了获取不同运行时间的曲线,可以调整$\alpha$的值或者在某些区间内设置惰行模式(即$F=0$)。例如,如果要求列车在最短运行时间上增加10s到达站台
实现代码
首先,需要定义一些常量和初始条件,如列车质量$m$、旋转质量因子$p$、坡度$i$、初始速度$v_0$、初始牵引力或制动力$F_0$、时间区间$[0,T]$、时间步长$\Delta t$等。这些参数可以根据具体的列车和路线进行设置。
m = 200000 # kg, 列车质量
p = 0.05 # 旋转质量因子
i = 0.01 # 坡度千分数
v0 = 0 # 初始速度
F0 = 30000 # 初始牵引力或制动力
T = 500 # s, 时间区间
dt = 1 # s, 时间步长
n = int(T/dt) # 时间步数
接下来,可以定义一些函数,如阻力函数$f(v)$、附加阻力函数$g(i)$、数值解微分方程的函数$ode_func(v, t, F)$等。这些函数可以根据具体的物理模型进行定义。
def f(v):
return 2.0895 + 0.0098*v + 0.006*v**2
def g(i):
return m*9.8*i
def ode_func(v, t, F):
dvdt = (F - f(v) - g(i)) / (m*(p+1))
return dvdt然后,可以使用欧拉法或者其他数值方法来求解微分方程。这里以欧拉法为例
# 初始化数组
v = [v0] * (n+1)
s = [0] * (n+1)
F = [F0] * (n+1)
t = [i*dt for i in range(n+1)]
# 求解微分方程
for i in range(n):
dvdt = ode_func(v[i], t[i], F[i])
v[i+1] = v[i] + dvdt*dt
F[i+1] = min(max(F[i] + alpha*dt, -760), 310)
s[i+1] = s[i] + (v[i] + v[i+1])/2 * dt根据求解出的速度、距离和牵引力或制动力,可以绘制速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线和能量消耗-距离曲线。具体的实现可以使用matplotlib等库进行绘制。
import matplotlib.pyplot as plt
# 绘制速度-距离曲线
plt.plot(s, v)
plt.xlabel('Distance (m)')
plt.ylabel('Speed (m/s)')
plt.title('Speed-Distance Curve')
plt