文章目录

一、常用内部函数
- 1. 常用数学函数
- 2. 矩阵的超越函数
- - 2.1 矩阵平方根
  - 2.2 矩阵对数
  - 2.3 矩阵指数
  - 2.4 普通矩阵函数
二、MATLAB 运算
- 1. 算术运算
- - 1.1 基本算术运算
  - 1.2 点运算
- 2. 关系运算
- 3. 逻辑运算
三、字符串
- 1. 字符串的表示
- 2. 字符串的操作
- - 2.1 字符串的执行
  - 2.2 字符串与数值之间的转换
  - 2.3 字符串的连接
  - 2.4 字符串的比较
  - 2.5 字符串的查找与替换
四、结构数据与单元数据
- 1. 结构数据
- - 1.1 结构数据的建立与引用
  - 1.2 结构成员的修改
- 2. 单元数据

一、常用内部函数

内部函数是由 MATLAB 系统根据一般用户的需要编制并提供给用户使用的一组程序，也被称为系统函数或库函数。

1. 常用数学函数

MATLAB 提供了许多数学函数，函数的自变量规定为矩阵变量，运算法则是将函数逐项作用于矩阵的元素上，因而运算的结果是一个与自变量具有相同维数和大小的矩阵，即结果矩阵与自变量矩阵同型。例如，我们可以对 A 矩阵中的每一个元素开更号。

>> A=[4,2;3,6]

A =

     4     2
     3     6

>> B=sqrt(A)

B =

    2.0000    1.4142
    1.7321    2.4495

MATLAB 中一些常见的数学函数如下表所示。

函数名	功能	函数名	功能
sin/sind	正弦函数，输入值为弧度/角度	abs	绝对值函数
cos/cosd	余弦函数，输入值为弧度/角度	rem	求余
tan/tand	正切函数，输入值为弧度/角度	mod	求模
asin/asind	反正弦函数，返回值为弧度/角度	fix	向零方向取整
acos/acosd	反余弦函数，返回值为弧度/角度	floor	不大于自变量的最大整数
atan/atand	反正切函数，返回值为弧度/角度	ceil	不小于自变量的最小整数
sinh/asinh	双曲正弦函数/反双曲正弦函数	round	四舍五入到最邻近的整数
cosh/acosh	双曲余弦函数/反双曲余弦函数	sign	符号函数
tanh/atanh	双曲正切函数/反双曲正切函数	gcd	最大公约数
sqrt	平方根函数	lcm	最小公倍数
log	自然对数函数	factorial	阶乘
log10	常用对数函数	isprime	判断是否为素数
log2	以2为底的对数函数	primes	生成素数列表
exp	自然指数函数	perms	生成所有排列
pow2	2 的幂	randperm	生成任意排列

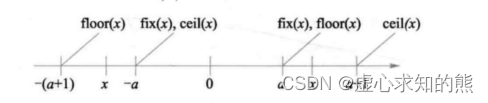
函数使用说明如下。
（1）三角函数有以弧度为单位的函数和以角度为单位的函数，以角度为单位的函数在函数名后面加 d，以示区别。
（2） abs 函数可以求实数的绝对值、复数的模、字符串的 ASCII 码值。例如, abs(-4)、abs(3+4i)、abs(‘a’)的值分别为 4、5、97。
（3）求余运算和求模运算有相同的地方但又不完全一致，主要的区别在于对负整数进行除法运算时的操作不同。
对于整数 a、b 来说，求余运算或求模运算的方法都是先求整数商 c=a/b，再求余数或模 r=a-c*b。求余运算在取 c 的值时，向 0 方向取整（fix 函数），而求模运算在计算 c 的值时，向负无穷方向取整（floor 函数）。
rem 与 mod 函数的区别是，当 b≠0 时，rem(a,b)=a-b.*fix(a./b)，而 mod(a,b)=a-b.*floor(a/b)；当 b=0 时，rem(a,0)=NaN, 而 mod(a,0)=a。
显然，如果 a、b 符号相同，那么 rem(a,b)=mod(a,b)。如果 a、b 符号相反，那么 mod(a,b)=rem(a,b)+b。
rem(a,b) 的符号与 a 相同，而 mod(a,b) 的符号与 b 相同。例如，rem(7,4)=mod(7,4)=3；rem(-7,- 4)= -mod(-7,-4)= -3；rem(7,-4)=3，而 mod(7,-4)= -1；rem(-7,4)= -3，而 mod(-7,4)=1。
（4）用于取整的函数有 fix、 floor、 ceil、 round，要注意它们的区别。round 函数的作用是四舍五入。设 a 为最靠近 x 的正整数（|x|≥a），则其余 3 个函数的区别可表示下图。

在这里插入图片描述

设 x=2.45，则 fix(x)、floor(x)、 ceil(x)、 round(x) 的结果分别是 2、2、3、 2。
设 x= -2.65，则 fix(x)、floor(x)、 ceil(x)、 round(x) 的结果分别是 -2、-3、 -2、 -3。
（5）关于符号函数。当 x<0 时， sign(x)=-1；当 x=0 时， sign(x)=0；当 x>0 时，sign(x)=1。

2. 矩阵的超越函数

MATLAB 提供了一些直接作用于矩阵的超越函数，这些函数名都在上述内部函数名之后缀以 m，并规定输入参数 A 必须是方阵。

2.1 矩阵平方根

sqrtm(A) 计算矩阵 A 的平方根 $\sqrt{A}$ 。例如：

>> A=[4,2;3,6];
>> B=sqrtm(A)

B =

    1.9171    0.4652
    0.6978    2.3823

>> B*B

ans =

    4.0000    2.0000
    3.0000    6.0000

若 A 为实对称正定矩阵，则一定能算出它的平方根。但某些矩阵，如 A=[0,1;0,0] 就得不到平方根。若矩阵 A 含有负的特征值，则 sqrtm(A) 将会得到一个复矩阵，例如：

>> A=[4,9;16,25];
>> eig(A)  %矩阵 A 的特征值

ans =

   -1.4452
   30.4452

>> B=sqrtm(A)

B =

   0.9421 + 0.9969i   1.5572 - 0.3393i
   2.7683 - 0.6032i   4.5756 + 0.2053i

2.2 矩阵对数

logm(A) 计算矩阵 A 的自然对数。此函数输入参数的条件与输出结果间的关系和函数 sqrtm(A) 完全一样，例如：


>> A=[4,9;1,5];
>> L=logm(A)

L =

    1.0639    2.4308
    0.2701    1.3340

2.3 矩阵指数

expm(A) 的功能是求矩阵指数 $e^{A}$ 。例如，对上面计算所得到的 A 的自然对数 L，求其矩阵指数 $B=e^{L}$ 。

>> B=expm(L)

B =

    4.0000    9.0000
    1.0000    5.0000

从这个结果可知，B 与 A 恰好是相同的，即 expm(A) 函数与 logm(A) 函数是互逆的。

2.4 普通矩阵函数

funm(A,@fun) 对方阵 A 计算由 fun 定义的函数的矩阵函数值。例如，当 fun 取 exp 时，funm(A,@fun) 可以计算矩阵 A 的指数，与 expm(A) 的计算结果一样。

>> A=[2,-1;1,0];
>> funm(A,@exp)

ans =

    5.4366   -2.7183
    2.7183         0

>> expm(A)

ans =

    5.4366   -2.7183
    2.7183         0

funm 函数可以用于 exp、log、sin、cos、sinh 和 cosh 等函数，但求矩阵的平方根只能用 sqrtm 函数。

二、MATLAB 运算

MATLAB 的运算都是针对矩阵而言的，既有矩阵意义下的运算，也有针对矩阵元素的运算。就运算的性质而言，有算术运算、关系运算和逻辑运算。

1. 算术运算

1.1 基本算术运算

MATLAB 的基本算术运算有 +（加）、-（减）、*（乘）、/（右除）、\（左除）、^（乘方）。
这些算术运算的运算规则不难理解，但必须注意，运算是在矩阵意义下进行的，单个数据的算术运算只是一种特例。
（1）矩阵加减运算。 假定有两个矩阵 A 和 B，则可以由 A+B 和 A-B 实现矩阵的加减运算。
运算规则是，若 A 和 B 同型，则可以执行矩阵的加减运算，A 和 B 的相应元素相加减。如果 A 与 B 不同型，则 MATLAB 将给出错误信息，提示两个矩阵的维数或大小不匹配。
一个标量也可以和矩阵进行加减运算，这时把标量和矩阵的每一一个元素进行加减运算。

>> x=[2,-1,0;3,2,-4];
>> y=x-1

y =

     1    -2    -1
     2     1    -5

（2）矩阵乘法。假定有两个矩阵 A 和 B，若 A 为 m×n 矩阵，B 为 n×p 矩阵，则 C=A×B 为 m×p 矩阵，其各个元素为 $C_{ij}=\sum_{k=1}^{n}a_{ik}.b_{kj}$
其中，i 是从 1 取到 m，j 是从 1 取到 p。

>> A=[1,2,3;4,5,6];
>> B=[1,2;3,0;7,4];
>> C=A*B

C =

    28    14
    61    32

矩阵 A 和 B 进行乘法运算，要求 A 的列数与 B 的行数相等，此时则称 A、B 矩阵是可乘的，或称 A 和 B 两矩阵维数和大小相容。如果两者的维数或大小不相容，则将给出错误信息，提示两个矩阵是不可乘的。

>> A=[10,20,30;40,50,60];
>> B=[1,3;4,8];
>> C=A*B
错误使用  * 
用于矩阵乘法的维度不正确。请检查并确保第一个矩阵中的列数与第二个矩阵中的行数匹配。要单独对矩阵的每个元素进行运算，请使用 TIMES
(.*)执行按元素相乘。

相关文档

说明 A 和 B 两矩阵维数或大小不相容，不能进行矩阵乘法运算。
在 MATLAB 中，还可以进行矩阵和标量相乘运算，标量可以是乘数也可以是被乘数。矩阵和标量相乘是矩阵中每个元素与此标量相乘。
（3）矩阵除法。在 MATLAB 中，有两种矩阵除法运算：\ 和 /，分别表示左除和右除。如果 A 矩阵是非奇异方阵，则 A\B 和 B/A 运算可以实现。
A\B 等效于 A 的逆左乘 B 矩阵，也就是 inv(A) * B；而 B/A 等效于 A 矩阵的逆右乘 B 矩阵，也就是 B * inv(A)。
对于含有标量的运算，两种除法运算的结果相同，如 3/4 和 4\3 有相同的值，都等于 0.75。又如，设 a=[10.5,25]，则 a/5= -5\a=[2.1000 5.0000]。
对于矩阵来说，左除和右除表示两种不同的除数矩阵和被除数矩阵的关系。对于矩阵运算，一般 A\B≠B/A。

>> A=[1,2,3;4,2,6;7,4,9];
>> B=[4,3,2;7,5,1;12,7,92];
>> C1=A/B

C1 =

    7.9623   -4.2453   -0.0943
   -4.5472    2.9434    0.1321
   -5.1321    3.6415    0.1698

>> C2=A\B

C2 =

    0.5000   -0.5000   44.5000
    1.0000    0.0000   46.0000
    0.5000    1.1667  -44.8333

显然，C1≠C2。
（4）矩阵的乘方。一个矩阵的乘方运算可以表示成 A^x，要求 A 为方阵，x 为标量。

>> A=[1,2,3;4,5,6;7,8,0];
>> A^2

ans =

    30    36    15
    66    81    42
    39    54    69

显然，A^2 即 A*A。
矩阵的开方运算是相当困难的，但有了计算机，这种运算就不再显得那么麻烦了，我们可以利用计算机方便地求出一个矩阵的方根。

>> A=[1,2,3;4,5,6;7,8,0];
>> A^0.1

ans =

   0.9750 + 0.2452i   0.1254 - 0.0493i   0.0059 - 0.0604i
   0.2227 - 0.0965i   1.1276 + 0.1539i   0.0678 - 0.1249i
   0.0324 - 0.1423i   0.0811 - 0.1659i   1.1786 + 0.2500i

1.2 点运算

在 MATLAB 中，有一种特殊的运算，因为其运算符是在有关算术运算符前面加点，所以叫点运算。
点运算符有 .*、./、.\ 和 .^。两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵同型。

>> A=[1,2,3;4,5,6;7,8,9];
>> B=[-1,0,1;1,-1,0;0,1,1];
>> C=A.*B

C =

    -1     0     3
     4    -5     0
     0     8     9

A .* B 表示 A 与 B 对应元素之间相乘，与 A * B 是两个截然不同的概念。
同时，如果 A、B 两矩阵同型，则 A./B 表示 A 矩阵除以 B 矩阵的对应元素。B.\A 等价于 A./B。

>> A=[1,2,3;4,5,6];
>> B=[-2,1,3;-1,1,4];
>> C1=A./B

C1 =

   -0.5000    2.0000    1.0000
   -4.0000    5.0000    1.5000
   
>> C2=B.\A

C2 =

   -0.5000    2.0000    1.0000
   -4.0000    5.0000    1.5000

显然，A./B 和 B.\A 值相等。这与前面介绍的矩阵的左除、右除是不一样的。
若两个矩阵同型，则A.^B 表示两矩阵对应元素进行乘方运算。其中，指数可以是标量，底数也可以是标量。

>> A=[1,2,3];
>> B=[4,5,6];
>> C=A.^B

C =

     1    32   729

>> C1=A.^2

C1 =

     1     4     9

>> C2=2.^[A,B]

C2 =

     2     4     8    16    32    64

这里需要注意的是，点运算是 MATLAB 中一个特殊的运算符。例如，当 x=0.1、0.4、0.7、1 时，分别求 $y=\sin x\cos x$ 的值，命令应当写成

>> x=0.1:0.3:1;
>> y=sin(x).*cos(x)

y =

    0.0993    0.3587    0.4927    0.4546

其中，y 的表达式中必须时点乘运算。如果 x 只有一个值，则用乘法运算即可。

2. 关系运算

MATLAB 提供了 6 种关系运算符: <（小于）、<=（小于等于）、>（大于）、>=（大于等于）、==（等于）、~=（不等于）。它们的含义不难理解，但要注意其书写方法与数学中的不等式符号不尽相同。
MATLAB 还提供了与 6 种关系运算符对应的函数 It、le、 gt、 ge、 eq、 ne。
关系运算符的运算法则如下。
（1）当两个比较量是标量时，直接比较两数的大小。若关系成立，关系表达式结果为 1，否则为 0。

>> 12>3

ans =

  logical

   1

>> eq(2,3)

ans =

  logical

   0

（2）当参与比较的量是两个同型的矩阵时，比较是对两矩阵相同位置的元素按标量关系运算规则逐个进行，并给出元素比较结果。最终的关系运算的结果是一个与原矩阵同型的矩阵，它的元素由 0 或 1 组成。
（3）当参与比较的一个是标量，而另一个是矩阵时，则把标量与矩阵的每一个元素按标量关系运算规则逐个比较，并给出元素比较结果。最终的关系运算的结果是一个与原矩阵同型的矩阵，它的元素由 0 或 1 组成。
例如，我们产生 5 阶随机方阵 A，其元素为 [10,90] 区间的随机整数，然后判断 A 的元素是否能被 3 整除。

>> A=fix((90-10+1)*rand(5)+10)

A =

    75    17    22    21    63
    83    32    88    44    12
    20    54    87    84    78
    83    87    49    74    85
    61    88    74    87    64

>> P=rem(A,3)==0  %等价于 P=eq(rem(A,3),0)

P =

  5×5 logical 数组

   1   0   0   1   1
   0   0   0   0   1
   0   1   1   1   1
   0   1   0   0   0
   0   0   0   1   0

其中，rem(A,3) 是矩阵 A 的每个元素除以 3 的余数矩阵。判断余数矩阵是否为 0 时，0 被扩展为与 A 同型的零矩阵，P 是比较的结果矩阵。
此外，MATLAB 还提供了一些关系运算函数，如下表所示。

函数名	含义
all	若向量的所有元素非零，则结果为 1，否则为 0
any	若向量中任何一个元素非零，则结果为 1，否则为 0
exist	检查变量在工作空间中是否存在，若存在，则结果为 1，否则为 0
find	找出向量或矩阵中非零元素的位置
isempty	若被查变量是空矩阵，则结果为 1，否则为 0
isinf	若元素是 ±tinf，则结果矩阵相应位置元素取 1，否则取 0
isnan	若元素是 nan，则结果矩阵相应位置元素取 1，否则取 0
isfinite	若元素值大小有限，则结果矩阵相应位置元素取 1，否则取 0
isinteger	若被查变量是整型，则取 1，否则取 0
isnumeric	若被查变量是数值型，则取 1，否则取 0
isreal	若被查变量是实数，则取 1，否则取 0
isfloat	若被查变量是浮点型，则取 1，否则取 0\

例如，我们建立矩阵 A，然后找出大于 4 的元素的位置，并输出相应位置的元素。

>> A=[4,-65,-54,0,6;56,0,67,-45,0]

A =

     4   -65   -54     0     6
    56     0    67   -45     0

>> k=find(A>4)

k =

     2
     6
     9

>> A(k)

ans =

    56
    67
     6

这里需要注意的是，find 函数得到的矩阵元素的位置是以相应元素的序号来表示的。

3. 逻辑运算

MATLAB 提供了 3 种逻辑运算符：&（与）、|（或）和 ~（非）。此外，还提供了 4 个逻辑运算函数：and(a,b)、 or(a,b)、 not(a) 和 xor(a,b)，分别代表与、或、非、异或运算。
在逻辑运算中，非零元素为真，用 1 表示；零元素为假，用 0 表示。
设参与逻辑运算的是两个标量 a 和 b，那么，逻辑运算的含义如下。
（1） a&b 或函数 and(a, b)：当 a、b 全为非零时，结果为 1；a、b 只要有一个为零则结果为 0。
（2） a|b 或函数 or(a,b)：当 a、b 中只要有一个非零，结果为 1；a、b 全为零时结果为 0。
（3）~a 和函数 not(a)：当 a 是零时，结果为 1；当 a 非零时，结果为 0。
（4）函数 xor(a,b)：当 a、b 的值不同时，结果为 1；当 a、b 的值相同时，结果为 0。
逻辑运算还有以下运算法则。
（1）若参与逻辑运算的是两个同型矩阵，那么运算将对矩阵相同位置上的元素按标量规则逐个进行。最终运算结果是一个与原矩阵同型的矩阵，其元素由 1 或 0 组成。
（2）若参与逻辑运算的一个是标量，一个是矩阵，那么运算将在标量与矩阵中的每个元素之间按标量规则逐个进行。最终运算结果是一个与矩阵同型的矩阵，其元素由 1 或 0 组成。
（3 ）逻辑非是单目运算符，也服从矩阵运算规则。
在算术运算、关系运算和逻辑运算中，算术运算优先级最高，逻辑运算优先级最低。

三、字符串

在 MATLAB 中，有两种基本的数据类型，一个是数值型数据，一个是字符型数据或称字符串数据。
数值型数据比较好理解，是指能参与数值运算的数据，又分为整型、浮点型和复数型。
字符型数据在日常应用中则不太强调，但却是大量存在的，例如统计一篇英文文章中不同英文字母出现的次数，按姓名排序，等等。字符串数据由若干个字符组成，这些字符可以是计算机系统中允许使用的任何字符。

1. 字符串的表示

在 MATLAB 中，字符串是单引号括起来的字符序列。

>> x='yan zi 22'

x =

    'yan zi 22'

若字符串中的字符含有单引号，则该单引号字符要用两个单引号来表示。

>> 'I ''m a student.'

ans =

    'I 'm a student.'

MATLAB 将一个字符串当作一个行向量，每个元素对应一个字符，其引用方法和数值向量相同。

>> A='ABCDEF';
>> A(1:3)

ans =

    'ABC'

也可以建立多行字符串，形成字符串矩阵。

>> A=['abcdef';'123456'];
>> A(2,3)

ans =

    '3'

需要注意的是，这里要求各行字符数要相等。为此，有时不得不用空格来调节各行的长度，使它们彼此相等。
例如，我们建立一个字符串向量，然后对该向量做如下处理。
（1）取第 1~5 个字符组成的子字符串。
（2）将字符串倒过来重新排列。
（3）将字符串中的小写字母变成相应的大写字母，其余字符不变。
（4）统计字符串中小写字母的个数。

>> A='ABc123d4e56Fg9';
>> A1=A(1:5)

A1 =

    'ABc12'

>> A2=A(end:-1:1)

A2 =

    '9gF65e4d321cBA'

>> k=find(A>='a'&A<='z');
>> A(k)=A(k)-('a'-'A')

A =

    'ABC123D4E56FG9'

>> length(k)

ans =

     4

2. 字符串的操作

2.1 字符串的执行

与字符串有关的一个重要函数是 eval，它的作用是把字符串的内容作为对应的 MATLAB 命令来执行，其调用格式如下：

>> eval(s)

其中，s 是字符串。

>> t=pi;
>> m='[t,sin(t),cos(t)]';
>> y=eval(m)

y =

    3.1416    0.0000   -1.0000

2.2 字符串与数值之间的转换

字符串是以 ASCII 码形式存储的，abs 和 double 函数都可以用来获取字符串矩阵所对应的 ASCII 码数值矩阵。char 函数可以把 ASCII 码矩阵转换为字符串矩阵。

>> s1='MATLAB';
>> a=abs(s1)

a =

    77    65    84    76    65    66

>> b=double(s1)

b =

    77    65    84    76    65    66

>> char(a+32)

ans =

    'matlab'

MATLAB 还有许多用于字符串和数值数据之间转换的函数。
setstr 函数将 ASCII 码值转换成对应的字符。
str2num 函数或 str2double 函数将数字字符串转换成数值。
num2str 函数将数值转换成字符串。
int2str 函数将整数转换成字符串。

2.3 字符串的连接

在 MATLAB 中，要将两个字符串连接在一起，有两种常见方法：一是用字符串向量，二是用 strcat 函数。
用字符串向量可以将若干个字符串连接起来，即用中括号将若干个字符串括起来，从而得到一个更长的字符串。

>> f=70;
>> c=(f-32)/1.8;
>> ['Room temperature is ',num2str(c),' degree C.']

ans =

    'Room temperature is 21.1111 degree C.'

strcat 函数可以将若干个字符串连接起来。

>> strcat('yan','zi','22')

ans =

    'yanzi22'

2.4 字符串的比较

字符串的比较有两种方法，利用关系运算符或字符串比较函数。
当两个字符串拥有相同的长度时，可以利用关系运算符对字符串进行比较，比较的规则是按 ASCII 值大小逐个字符进行比较，比较的结果是一一个数值向量，其元素为对应字符比较的结果。

>> 'www0'>='W132'

ans =

  1×4 logical 数组

   1   1   1   0

字符串比较函数用于判断字符串是否相等，有 4 种比较方式，函数如下。
（1） strcmp(s1,s2)：用来比较字符串 s1 和 s2 是否相等，如果相等，返回 1, 否则返回 0。
（2） strncmp(s1,s2,n)：用来比较前 n 个字符是否相等，如果相等，返回 1，否则返回 0。
（3） strcmpi(s1,s2)：在忽略字母大小写前提下，比较字符串 s1 和 s2 是否相等，如果相等，返回 1,否则返回 0。
（4） strnempi(s1,s2,n)：在忽略字符串大小写前提下，比较前 n 个字符是否相等，如果相等，返回 1，否则返回 0。

>> strcmp('www0','W123')

ans =

  logical

   0
 
>> strncmpi('ww0','W12',1)

ans =

  logical

   1

2.5 字符串的查找与替换

MATLAB 提供了许多函数，用来对字符串中的字符进行查找与替换。常用的有以下两个。
（1） findstr(s1,s2)：返回短字符串在长字符串中的开始位置（s1，s2 的顺序没有要求）。

>> p1=findstr('this is a test','is')

p1 =

     3     6

>>  p2=findstr('is','this is a test')

p2 =

     3     6

短字符串 is 在长字符串 this is a test 中出现两次，开始位置分别为 3 和 6。
（2） strep(1,s2,s3)：将字符串 s1 中的所有子字符串 s2 替换为字符串 s3。

>> p3=strrep('this is a test','test','success')

p3 =

    'this is a success'

四、结构数据与单元数据

MATLAB 新增加了两种数据类型：结构数据类型和单元数据类型。
这两种数据类型均是将不同的相关数据集成到一个单-的变量中，使得大量的相关数据的处理
与引用变得简单、方便。

1. 结构数据

个人感觉可以参考 C++ 中的结构体。
结构数据类型把一组类型不同而逻辑上相关的数据组成一个有机的整体，以便于管理和引用。例如要存储学生的基本信息就可采用结构数据类型。

1.1 结构数据的建立与引用

结构矩阵的元素可以是不同的数据类型，它能将一组具有不同属性的数据纳入到一个统一的变量名下进行管理。建立一个结构矩阵可以采用给结构成员赋值的办法，其格式如下：

    结构矩阵名.成员名=表达式

其中，表达式应理解为矩阵表达式。例如，我们要建立含有 3 个元素的结构矩阵 a，命令如下：

>> a(1).x1=10;a(1).x2='liu';a(1).x3=[11,21;34,78];
>> a(2).x1=12;a(2).x2='wang';a(2).x3=[34,191;27,578];
>> a(3).x1=14;a(3).x2='cai';a(3).x3=[13,180;57,231];

这里需要注意的是，结构矩阵元素的成员也可以是结构数据。

>> a(2).x1.x11=90;a(2).x1.x12=12;a(2).x1.x13=30;

以上建立的结构矩阵 a 含有 3 个元素，每个元素又含有 3 个成员，成员 a(2).x1 又是含有 3 个成员的结构数据。
对结构数据的引用，可以引用其成员，也可以引用结构矩阵的元素或结构变量。

 >> a(2).x3

ans =

    34   191
    27   578

>> a(2)

ans = 

  包含以下字段的 struct:

    x1: 12
    x2: 'wang'
    x3: [2×2 double]

>> a

a = 

  包含以下字段的 1×3 struct 数组:

    x1
    x2
    x3

引用结构矩阵元素的成员时，显示其值。引用结构矩阵元素时，显示成员名和它的值，但成员是矩阵时，不显示其具体内容，只显示成员矩阵大小参数。引用结构矩阵时，只显示结构矩阵的大小参数和成员名。

1.2 结构成员的修改

可以根据需要增加或删除结构的成员。例如，我们要给结构矩阵 a 增加一一个成员 x4，可给 a 中任意一个元素增加成员 x4，命令如下：

>> a(1).x4='410075';

但其他成员均为空矩阵，可以使用赋值语句给它赋确定的值。
要删除结构的成员，则可以使用 rmfield 函数来完成。例如，要删除成员 x4，命令如下：

>> a=rmfield(a,'x4');

2. 单元数据

单元数据类型与结构数据类型类似，也是把不同属性的数据放在一个变量中。不同的是，结构矩阵的各个元素下有成员，每个成员都有自己的名字，对成员的引用如下：

    结构矩阵名.成员名

而单元矩阵的各个元素就是不同类型的数据，用带有大括号下标的形式引用单元矩阵元素。
建立单元矩阵和一般矩阵相似，只是矩阵元素用大括号括起来。

>> a={10,'liu',[11,21;34,78];12,'wang',[34,191;27,578];14,'cai',[13,890;67,231]}

a =

  3×3 cell 数组

    {[10]}    {'liu' }    {2×2 double}
    {[12]}    {'wang'}    {2×2 double}
    {[14]}    {'cai' }    {2×2 double}

可以用带有大括号下标的形式引用单元矩阵元素。

>> a{3,3}

ans =

    13   890
    67   231

单元矩阵的元素可以是结构或单元数据。例如，我们先建立结构变量 y，给上面建立的单位矩阵 a 的元素 a{3,4} 赋值，命令如下：

>> y.x1=34;y.x2=56;
>> a{3,4}=y;

可以使用 celldisp 函数来显示整个单元矩阵，如 celldisp(a)。还可以删除单元矩阵中某个元素，如删除 a 的第 3 个元素，其命令如下：

>> a(3)=[]

a =

  1×11 cell 数组

  列 1 至 8

    {[10]}    {[12]}    {'liu'}    {'wang'}    {'cai'}    {2×2 double}    {2×2 double}    {2×2 double}

  列 9 至 11

    {0×0 double}    {0×0 double}    {1×1 struct}